| Date | May 2017 | Marks available | 1 | Reference code | 17M.3ca.hl.TZ0.5 |
| Level | HL only | Paper | Paper 3 Calculus | Time zone | TZ0 |
| Command term | Explain | Question number | 5 | Adapted from | N/A |
Question
Consider the curve \(y = \frac{1}{x},{\text{ }}x > 0\).
Let \({U_n} = \sum\limits_{r = 1}^n {\frac{1}{r} - \ln n} \).
By drawing a diagram and considering the area of a suitable region under the curve, show that for \(r > 0\),
\[\frac{1}{{r + 1}} < \ln \left( {\frac{{r + 1}}{r}} \right) < \frac{1}{r}.\]
Hence, given that \(n\) is a positive integer greater than one, show that
\(\sum\limits_{r = 1}^n {\frac{1}{r} > \ln (1 + n)} \);
Hence, given that \(n\) is a positive integer greater than one, show that
\(\sum\limits_{r = 1}^n {\frac{1}{r} < 1 + \ln n} \).
Hence, given that \(n\) is a positive integer greater than one, show that
\({U_n} > 0\);
Hence, given that \(n\) is a positive integer greater than one, show that
\({U_{n + 1}} < {U_n}\).
Explain why these two results prove that \(\{ {U_n}\} \) is a convergent sequence.
Markscheme
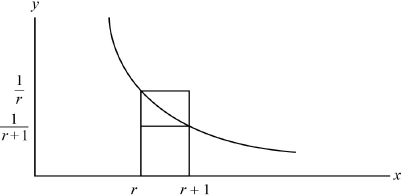
A1
Note: Curve, both rectangles and correct \(x\)values required.
area of rectangles \(\frac{1}{r}\) and \(\frac{1}{{1 + r}}\) A1
Note: Correct values on the \(y\)-axis are sufficient evidence for this mark if not otherwise indicated.
in the above diagram, the area below the curve between \(x = r\) and \(x = r + 1\) is between the areas of the larger and smaller rectangle
or \(\frac{1}{{r + 1}} < \int\limits_r^{r + 1} {\frac{{{\text{d}}x}}{x} < \frac{1}{r}} \) (R1)
integrating, \(\int_r^{r + 1} {\frac{{{\text{d}}x}}{x} = [\ln x]_r^{r + 1}\,\,\,\left( { = \ln (r + 1) - \ln (r)} \right)} \) A1
\(\frac{1}{{r + 1}} < \ln \left( {\frac{{r + 1}}{r}} \right) < \frac{1}{r}\) AG
[4 marks]
summing the right-hand part of the above inequality from \(r = 1\) to \(r = n\),
\(\sum\limits_{r = 1}^n {\frac{1}{r}} > \sum\limits_{r = 1}^n {\ln \left( {\frac{{r + 1}}{r}} \right)} \) M1
\( = \ln \left( {\frac{2}{1}} \right) + \ln \left( {\frac{3}{2}} \right) + \ldots + \ln \left( {\frac{n}{{n - 1}}} \right) + \ln \left( {\frac{{n + 1}}{n}} \right)\) (A1)
EITHER
\( = \ln \left( {\frac{2}{1} \times \frac{3}{2} \times \ldots \times \frac{n}{{n - 1}} \times \frac{{n + 1}}{n}} \right)\) A1
OR
\(\ln 2 - \ln 1 + \ln 3 - \ln 2 + \ldots + \ln (n + 1) - \ln (n)\) A1
\( = \ln (n + 1)\) AG
[3 marks]
\(\sum\limits_{r = 1}^n {\frac{1}{r} = 1 + \frac{1}{2} + \frac{1}{3} + \ldots + \frac{1}{n} < 1 + \ln \left( {\frac{2}{1}} \right) + \ln \left( {\frac{3}{2}} \right) + \ldots + \ln \left( {\frac{n}{{n - 1}}} \right)} \) M1A1A1
\(\left( {1 + \sum\limits_{r = 1}^{n - 1} {\frac{1}{{r + 1}} < 1 + \sum\limits_{r = 1}^{n - 1} {\ln \left( {\frac{{r + 1}}{r}} \right)} } } \right)\)
Note: M1 is for using the correct inequality from (a), A1 for both sides beginning with 1, A1 for completely correct expression.
Note: The 1 might be added after the sums have been calculated.
\( = 1 + \ln n\) AG
[3 marks]
from (b)(i) \({U_n} > \ln (1 + n) - \ln n > 0\) A1
[1 mark]
\({U_{n + 1}} - {U_n} = \sum\limits_{r = 1}^{n + 1} {\frac{1}{r} - \ln (n + 1) - \sum\limits_{r = 1}^n {\frac{1}{r} + \ln n} } \) M1
\( = \frac{1}{{n + 1}} - \ln \left( {\frac{{n + 1}}{n}} \right)\) A1
\( < 0\) (using the result proved in (a)) A1
\({U_{n + 1}} < {U_n}\) AG
[3 marks]
it follows from the two results that \(\{ {U_n}\} \) cannot be divergent either in the sense of tending to \( - \infty \) or oscillating therefore it must be convergent R1
Note: Accept the use of the result that a bounded (monotonically) decreasing sequence is convergent (allow “positive, decreasing sequence”).
[1 mark]

