DP Mathematics: Analysis and Approaches Questionbank

Topic 4—Statistics and probability
Description
[N/A]Directly related questions
-
20N.1.SL.TZ0.S_1a.i:
Find the value of .
-
20N.1.SL.TZ0.S_8e:
The first athletes that completed the race won a prize.
Given that an athlete took between and minutes to complete the race, calculate the probability that they won a prize.
-
20N.2.SL.TZ0.S_2b:
Using the regression equation, estimate the number of hot chocolates that Lucy will sell on a day when the maximum temperature is .
-
20N.1.SL.TZ0.T_7c:
Write down a second equation in and .
-
20N.2.SL.TZ0.T_2d.i:
Find the probability that a randomly selected student visited the rollercoasters.
-
20N.2.SL.TZ0.T_2e:
Hence determine whether the events in parts (d)(i) and (d)(ii) are independent. Justify your reasoning.
-
20N.2.SL.TZ0.T_6a:
Sketch a diagram to represent this information.
-
20N.2.SL.TZ0.T_6e:
Find the probability he plays between and in one game and more than in the other game.
-
EXN.2.SL.TZ0.8a:
By stating and solving an appropriate equation, show, correct to two decimal places, that .
-
21M.2.SL.TZ1.2b:
Use this model to predict the value of when .
-
21M.2.SL.TZ1.2d:
Draw the line of best fit on the scatter diagram.
-
21M.1.SL.TZ1.9c.ii:
Hence, find the range of possible values of .
-
21M.2.AHL.TZ2.6b:
Show that .
-
21M.2.SL.TZ2.8d:
Find the expected number of flights that will have a flight time of more than minutes.
-
21M.2.SL.TZ2.1a.i:
Find the value of and the value of .
-
21M.2.SL.TZ2.4b:
Find the probability that the student is involved in theatre, but does not play a sport.
-
21N.2.SL.TZ0.9b:
Find the value of and of .
-
21N.2.AHL.TZ0.7a:
Determine the value of .
-
22M.1.SL.TZ2.9e:
Find the value of , providing evidence for your answer.
-
22M.1.AHL.TZ2.8:
A continuous random variable has the probability density function
.
The following diagram shows the graph of for .
Given that , find an expression for the median of in terms of and .
-
22M.2.SL.TZ1.2b:
Find the standard deviation.
-
22M.2.SL.TZ2.9c:
Find the probability that she will be late to work at least one day next week.
-
EXM.2.SL.TZ0.1d.iii:
Explain why the value of makes it appropriate to find the equation of a regression line.
-
18M.1.SL.TZ1.S_2b:
One student sent k text messages, where k > 11 . Given that k is an outlier, find the least value of k.
-
18N.2.SL.TZ0.T_1a.i:
Use your graphic display calculator to write down , the mean project mark.
-
19M.1.SL.TZ1.T_2c:
Write down the range of the animal speeds.
-
19M.1.SL.TZ2.T_2a:
Find the equation of the regression line of on .
-
19M.1.SL.TZ2.T_6b.i:
Write down the interquartile range for this data.
-
19M.1.SL.TZ2.T_5a:
Using the given information, complete the following Venn diagram.
-
18N.2.SL.TZ0.S_1b.i:
the student does not take art class.
-
18N.2.SL.TZ0.T_2a.iii:
Find the number of students in the school that study both Biology and Mathematics.
-
18N.2.SL.TZ0.T_2b.ii:
Write down .
-
18N.2.SL.TZ0.T_2c.ii:
Find the probability that this student studies neither Biology nor Mathematics.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6e:
Find .
-
18M.1.SL.TZ2.S_3b.i:
Write down the value of the new mean.
-
18N.2.SL.TZ0.T_3a.i:
Find the median of the examination results.
-
17M.1.SL.TZ2.T_6c.i:
Use the graph to find the value of .
-
18M.1.SL.TZ1.T_4a.i:
For these data, find Pearson’s product-moment correlation coefficient, r.
-
16N.2.SL.TZ0.T_1b:
(i) , the mean number of hours spent on social media;
(ii) , the mean number of IB Diploma points.
-
18M.1.SL.TZ2.T_1b:
Draw the line of best fit, by eye, on the scatter diagram.
-
16N.2.SL.TZ0.T_1g:
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.
-
16N.1.AHL.TZ0.H_10b:
(i) show that ;
(ii) hence find .
-
19M.2.SL.TZ1.T_1c:
Plot and label the point M(, ) on the scatter diagram.
-
17N.1.SL.TZ0.T_7b:
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.
-
17N.1.SL.TZ0.T_7c:
Determine whether the events and are independent.
-
19M.2.SL.TZ2.S_9a:
Show that event A and event D are not independent.
-
19M.2.SL.TZ2.S_9b.ii:
Given that all passengers for a flight arrive on time, find the probability that the flight does not depart on time.
-
19M.1.SL.TZ1.S_9b:
Given that > −1.6, find the probability that z < 2.4 . Write your answer in terms of and .
-
19M.1.SL.TZ1.S_9d:
It is also known that P( > 2) = .
Find .
-
18N.1.SL.TZ0.S_9a.ii:
Find the probability, in terms of , that the game will end on her second draw.
-
19M.2.SL.TZ1.T_3g:
Calculate the expected number of teenagers that prefer cats.
-
19M.2.SL.TZ1.T_3h:
Use your graphic display calculator to find the -value for this test.
-
18M.2.SL.TZ2.T_2b.i:
Use the cumulative frequency curve to find the median distance.
-
18M.2.SL.TZ2.T_2f:
Find the value of m.
-
17M.2.SL.TZ1.T_5d:
Find the probability that this student scored a grade 5 or higher.
-
19M.2.SL.TZ2.T_1a:
Write down the null hypothesis, H0 , for this test.
-
19M.2.SL.TZ2.T_1d:
State whether or not H0 should be rejected. Justify your statement.
-
17N.2.SL.TZ0.S_7:
The heights of adult males in a country are normally distributed with a mean of 180 cm and a standard deviation of . 17% of these men are shorter than 168 cm. 80% of them have heights between and 192 cm.
Find the value of .
-
18N.2.SL.TZ0.S_9a:
A person is selected at random from Group X. Find the probability that their reaction time is greater than 0.65 seconds.
-
18M.1.SL.TZ1.T_13a.ii:
Find the probability that a student, chosen at random arrives between 45 minutes and 55 minutes after the school opens.
-
17N.2.SL.TZ0.T_4g:
Estimate the number of employees, from this 38, who are allergic to nuts.
-
17M.2.AHL.TZ1.H_9b:
Calculate .
-
17M.1.SL.TZ1.T_1c:
Write down the modal class.
-
17M.1.SL.TZ1.T_2a:
Calculate the percentage of the population of Ottawa that speak English but not French.
-
18M.2.SL.TZ1.S_9e:
The grocer selects two boxes at random.
Find the probability that the grocer buys more than half the oranges in each box.
-
18M.2.SL.TZ2.T_3d.ii:
For this test find the p-value.
-
18M.2.AHL.TZ2.H_3c:
Find the value of k for which P(μ − kσ < X < μ + kσ) = 0.5.
-
17N.2.SL.TZ0.S_8d.i:
Find the value of ;
-
16N.2.SL.TZ0.T_2a:
Draw a Venn diagram to represent the given information, using sets labelled , and .
-
17M.2.SL.TZ1.T_1b.i:
For the data from these seven species calculate , the Pearson’s product–moment correlation coefficient;
-
17M.2.SL.TZ1.T_1d:
Use your regression line to estimate the average weight of the brain of grey wolves.
-
16N.2.SL.TZ0.T_4d:
Calculate the value of .
-
16N.2.SL.TZ0.S_5a:
Given that 5.3% of newborn babies have a low birth weight, find .
-
19N.1.AHL.TZ0.H_1b:
Given that , find the value of .
-
19N.2.AHL.TZ0.H_10a:
Find, in terms of , the probability that lies between 1 and 3.
-
19N.2.SL.TZ0.S_7b:
Find the difference between the greatest possible expected value and the least possible expected value.
-
19M.1.AHL.TZ2.H_10c.i:
.
-
16N.2.SL.TZ0.S_8b:
During week 2, the students worked on a major project and they each spent an additional five hours browsing the Internet. For week 2, write down
(i) the mean;
(ii) the standard deviation.
-
16N.2.AHL.TZ0.H_11c:
Deduce that for .
-
18M.2.AHL.TZ1.H_10a:
Show that .
-
18M.1.SL.TZ2.S_8e:
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
-
19M.1.SL.TZ1.S_1a:
Find the value of .
-
18M.2.SL.TZ2.T_1e:
Find .
-
17M.2.SL.TZ2.S_10d:
Grant plays the game until he wins two prizes. Find the probability that he wins his second prize on his eighth attempt.
-
17M.2.SL.TZ2.S_10a.i:
Find .
-
17M.1.AHL.TZ1.H_10c.ii:
Hence state the interquartile range of .
-
17M.1.AHL.TZ1.H_10d:
Calculate .
-
18M.1.SL.TZ2.S_8c:
Find the probability that Pablo is late for work.
-
18M.2.SL.TZ2.T_1c.ii:
Find the value of y.
-
SPM.1.SL.TZ0.7f:
Travelling times of less than minutes are considered outliers.
Find the value of .
-
18M.1.AHL.TZ2.H_3b.i:
Find μ, the expected value of X.
-
20N.1.SL.TZ0.S_8d:
Find .
-
20N.2.SL.TZ0.S_2a.ii:
Write down the correlation coefficient.
-
20N.2.SL.TZ0.S_9a:
Find the probability that it will take Fiona between minutes and minutes to walk to the bus stop.
-
20N.1.SL.TZ0.T_3c:
On the grid below, draw a histogram for the data in the table.
-
20N.1.SL.TZ0.T_6c:
Find the probability that both balls chosen are labelled .
-
20N.1.SL.TZ0.T_7b:
Using this information, write down an equation in and .
-
20N.2.SL.TZ0.T_2b:
Find the number of students who visited at least two types of main attraction.
-
20N.2.SL.TZ0.T_2d.ii:
Find the probability that a randomly selected student visited the virtual reality rides.
-
EXN.2.SL.TZ0.8b:
Find the th percentile time to complete the jigsaw puzzle.
-
21M.2.SL.TZ1.3a:
Find the probability that a bag selected at random is rejected.
-
21M.1.SL.TZ2.7e.i:
Explain why this sampling method might not provide an accurate representation of the amount of time all of the students in the school spend doing homework.
-
21M.2.SL.TZ2.9a:
Find the value of .
-
21N.2.SL.TZ0.4a:
Find the probability that there is at least one defective lamp in the sample.
-
21N.2.AHL.TZ0.1c:
One of these eight students was disappointed with her result and wished she had practised more. Based on the given data, determine how her score could have been expected to alter had she practised an extra five hours per week.
-
22M.1.SL.TZ2.9d:
Determine the value of .
-
22M.2.SL.TZ1.6a:
Given that , find the value of .
-
22M.1.SL.TZ1.3b.i:
One of the adults surveyed is years old. Estimate the age of their eldest child.
-
SPM.2.AHL.TZ0.4a:
Find the value of a and the value of b.
-
SPM.2.AHL.TZ0.4b:
Find the value of p and the value of q.
-
SPM.2.SL.TZ0.8e:
A seashell selected at random has a length less than 26 mm.
Find the probability that its length is between 24.15 mm and 25 mm.
-
SPM.2.SL.TZ0.5a:
Find the value of a and the value of b.
-
17M.2.SL.TZ1.S_1a.ii:
Find the value of the range.
-
18M.1.SL.TZ1.T_6c.ii:
Using the table, calculate an estimate for the mean number of people being followed on the social media website by these 160 students.
-
18N.2.SL.TZ0.T_1b.ii:
Show that the point M (, ) lies on the regression line y on x.
-
18N.2.SL.TZ0.T_1d:
In his final IB examination Jerome scored 65.
Calculate the percentage error in Jerome’s estimated examination score.
-
17M.2.SL.TZ2.S_8c.i:
Find the coordinates of B.
-
19M.1.SL.TZ2.T_6a:
State what 13 represents in the given diagram.
-
17N.1.AHL.TZ0.H_10b.i:
Determine the mean of X.
-
18N.1.SL.TZ0.T_2c.i:
Calculate the lower quartile.
-
18N.1.SL.TZ0.T_8a:
Complete the tree diagram.
-
18N.2.SL.TZ0.S_1b.ii:
the student takes either art class or music class, but not both.
-
18N.2.SL.TZ0.T_2c.i:
Find the probability that this student studies Mathematics.
-
17M.1.SL.TZ1.S_10b:
Given that , find .
-
17M.1.SL.TZ1.S_10c:
Let , for . The graph of between and is rotated 360° about the -axis. Find the volume of the solid formed.
-
19M.2.SL.TZ2.S_1b:
Use the regression equation to estimate the BMI of an adult man whose waist size is 95 cm.
-
17M.1.SL.TZ1.S_4a.ii:
Write down the boiling temperature of the liquid.
-
18M.1.SL.TZ2.S_3a:
Find n.
-
18N.2.SL.TZ0.T_3d.i:
Calculate an estimate of the mean examination result.
-
17M.1.SL.TZ2.T_10b.i:
Find the probability that both light bulbs are not defective.
-
17M.1.SL.TZ2.T_10b.ii:
Find the probability that at least one of Francesco’s light bulbs is defective.
-
16N.1.SL.TZ0.T_12b:
Find the value of .
-
18M.2.SL.TZ1.S_8b:
Use the regression equation to estimate the value of y when x = 3.57.
-
19M.1.SL.TZ2.T_12b:
On the same grid, complete the cumulative frequency curve for these data.
-
16N.2.SL.TZ0.T_1c:
Plot the point on your scatter diagram and label this point M.
-
17N.1.SL.TZ0.T_5a:
Find the mean number of hours that the people surveyed watch television per week.
-
17M.2.SL.TZ2.T_3g:
Draw the regression line on on the scatter diagram.
-
17M.2.SL.TZ2.T_3h:
Use the equation of the regression line to estimate the least number of folders that the factory needs to sell in a month to exceed its production cost for that month.
-
18M.1.SL.TZ2.T_1c:
Using your line of best fit, estimate the physics test score for a student with a score of 20 in their mathematics test.
-
16N.2.SL.TZ0.T_1h:
Write down a reason why this estimate is not reliable.
-
19M.2.SL.TZ1.T_1e:
Use your graphic display calculator to find the equation of the regression line on .
-
17N.1.SL.TZ0.T_7a:
Complete the Venn diagram for these students.
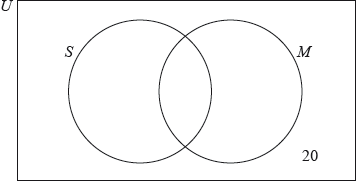
-
19M.2.SL.TZ2.S_9b.i:
Find .
-
19M.2.AHL.TZ2.H_10e:
Show that the expected number of occasions per year on which Steffi visits Will’s house and is not fed is at least 30.
-
18M.1.SL.TZ2.T_7a:
State the number of boys who answered questions in Portuguese.
-
18M.2.SL.TZ1.T_5e:
120 contestants attempted this game.
Find the expected number of contestants who fell into a trap while attempting to pass through a door in the third wall.
-
19M.2.SL.TZ1.S_10c.ii:
Hence, find the value of .
-
18N.2.SL.TZ0.S_2b:
Another athlete on this sports team has a hand length of 21.5 cm. Use the regression equation to estimate the height of this athlete.
-
19M.1.SL.TZ2.S_1a:
Find the value of .
-
19M.1.SL.TZ2.T_14c:
To stimulate reasonable pricing, the city offers a free permit to the sellers whose price of a kilogram of tomatoes is in the lowest 20 %.
Find the highest price that a seller can charge and still receive a free permit.
-
19M.2.SL.TZ1.T_3b:
Write down the modal number of pets.
-
18M.2.SL.TZ2.T_2a:
Find the number of buses that travelled a distance between 15000 and 20000 kilometres.
-
18M.2.SL.TZ2.T_2c:
Hence write down the interquartile range.
-
17M.2.SL.TZ1.T_5e:
Given that the first student chosen at random scored a grade 5 or higher, find the probability that both students scored a grade 6.
-
19M.2.SL.TZ2.T_1e.i:
Find the probability that the student does not take the Spanish class.
-
19M.1.SL.TZ1.T_11a:
In the following table, write down the letter of the corresponding graph next to the given mean and standard deviation.
-
18M.1.SL.TZ1.T_13a.i:
Find the probability that a student, chosen at random arrives at least 60 minutes after the school opens.
-
18M.2.SL.TZ1.S_2c:
The die is rolled 80 times. On how many rolls would you expect to obtain a three?
-
17N.2.SL.TZ0.T_4b:
Find the probability that both people chosen are not allergic to nuts.
-
17M.1.SL.TZ2.S_3c:
Find .
-
17M.1.SL.TZ2.T_11c:
Estimate the interquartile range of the distribution.
-
17M.2.AHL.TZ2.H_3c:
Calculate the new value of .
-
17M.1.SL.TZ1.T_2b:
Calculate the number of people in Ottawa that speak both English and French.
-
18M.2.SL.TZ1.T_2a:
State the alternative hypothesis.
-
18M.2.SL.TZ1.T_2e:
State, with a reason, whether you would reject the null hypothesis.
-
18M.2.SL.TZ1.T_2h:
Two flights are chosen at random from those which were slightly delayed.
Find the probability that each of these flights travelled at least 5000 km.
-
18M.2.SL.TZ2.T_3b.i:
Sketch a normal curve to represent this probability.
-
18M.2.SL.TZ2.T_3c:
Given that P(W > k) = 0.225 , find the value of k.
-
18M.2.AHL.TZ1.H_4b:
Eight wolves are independently selected at random and their ages recorded.
Find the probability that more than six of these wolves are at least 5 years old.
-
16N.2.AHL.TZ0.H_8a:
Find and .
-
16N.2.AHL.TZ0.H_8b:
Find .
-
17M.2.SL.TZ1.T_1c:
Write down the equation of the regression line on , in the form .
-
17M.2.SL.TZ1.T_1e:
Find the percentage error in your estimate in part (d).
-
16N.2.SL.TZ0.T_4c:
Calculate the manufacturer’s expected daily recycling cost.
-
19N.1.AHL.TZ0.H_1a:
Find the value of .
-
19N.2.SL.TZ0.S_1a:
Write down the value of and of .
-
19M.2.AHL.TZ1.H_9b.i:
Find the expected number of cakes sold on a typical day.
-
16N.2.AHL.TZ0.H_11a:
Show that and .
-
18M.1.SL.TZ2.T_9b.i:
Shade, on the Venn diagram, the region represented by the set .
-
16N.1.SL.TZ0.S_5a:
Find .
-
18M.1.SL.TZ2.T_9a.i:
Write down an expression, in set notation, for the shaded region represented by Diagram 1.
-
19M.2.AHL.TZ2.H_3a:
Complete the given probability tree diagram for Iqbal’s three attempts, labelling each branch with the correct probability.
-
17M.1.SL.TZ1.T_4a:
Write down the number of sporting activities offered by the school during its school year.
-
17M.2.AHL.TZ2.H_10a:
Show that and .
-
19M.1.SL.TZ1.S_1c:
Find .
-
17M.2.SL.TZ2.S_10b.ii:
Explain why the probability of drawing three white marbles is .
-
17M.2.AHL.TZ2.H_10e:
Find .
-
18M.2.SL.TZ2.T_1d:
Find the number of employees who, in the last year, did not travel to work by car, bicycle or public transportation.
-
20N.2.AHL.TZ0.H_9c:
A packet is randomly selected. Given that the packet has a weight greater than , find the probability that it has a weight greater than .
-
20N.1.SL.TZ0.S_8a:
Find the value of .
-
20N.1.SL.TZ0.S_8c:
Find the value of .
-
20N.2.SL.TZ0.S_9c:
Find the probability that the bus journey takes less than minutes.
-
20N.2.SL.TZ0.S_9d:
Find the probability that Fiona will arrive on time.
-
20N.1.SL.TZ0.T_7d.i:
Using your answers to parts (b) and (c), find the height of Flower .
-
20N.2.SL.TZ0.T_6b:
Show that .
-
21M.1.SL.TZ1.4a:
Find the minimum possible value of .
-
21M.2.AHL.TZ1.7a:
Show that .
-
21M.1.SL.TZ2.7a:
Find the median number of hours per week these Year 12 students spend doing homework.
-
21M.2.SL.TZ2.8c:
Given that a flight between the two cities takes longer than minutes, find the probability that it takes less than minutes.
-
21M.2.SL.TZ2.4c:
Find .
-
21M.2.SL.TZ2.9b:
Determine whether this lottery is a fair game in the first week. Justify your answer.
-
18M.2.SL.TZ1.T_5c:
Copy the probability tree diagram and write down the relevant probabilities along the branches.
-
21N.2.SL.TZ0.1b:
The relationship between the variables can be modelled by the regression equation . Write down the value of and the value of .
-
21N.2.SL.TZ0.9c.ii:
large.
-
21N.2.SL.TZ0.9d:
The selling prices of the different categories of avocado at this supermarket are shown in the following table:
The supermarket pays the farm for the avocados and assumes it will then sell them in exactly the same proportion as purchased from the farm.
According to this model, find the minimum number of avocados that must be sold so that the net profit for the supermarket is at least .
-
21N.2.SL.TZ0.9c.iii:
premium.
-
21N.2.AHL.TZ0.7b:
Given that , determine the value of .
-
22M.1.SL.TZ1.3a:
Find the largest value of that would not be considered an outlier.
-
22M.1.SL.TZ2.9a:
Show that and .
-
22M.1.SL.TZ2.9c:
Assuming that rolls of the die are independent, find the probability that Nicky wins the game.
-
22M.2.SL.TZ1.9c.ii:
Given that a randomly selected muffin weighs less than , find the probability that it is chocolate.
-
22M.2.SL.TZ2.4:
Events and are independent and .
Given that , find .
-
SPM.1.AHL.TZ0.7:
A continuous random variable X has the probability density function given by
.
Find P(0 ≤ X ≤ 3).
-
SPM.2.AHL.TZ0.6a:
Find E(T).
-
SPM.2.SL.TZ0.4a:
The die is tossed five times. Find the probability of obtaining at most three “sixes”.
-
EXM.2.SL.TZ0.1d.i:
Calculate Pearson’s product moment correlation coefficient, .
-
18M.1.SL.TZ1.S_2a:
Find the value of the interquartile range.
-
19M.1.SL.TZ1.T_2a:
State whether speed is a continuous or discrete variable.
-
19M.1.SL.TZ1.T_2b:
Write down the median speed for these animals.
-
19M.1.SL.TZ1.T_2d.ii:
For these eight animals write down the standard deviation.
-
17M.1.SL.TZ1.S_4a.i:
Write down the independent variable.
-
19M.1.SL.TZ1.T_12a:
Find the probability that both spins are yellow.
-
19M.2.SL.TZ2.S_1a.ii:
Find the correlation coefficient.
-
17M.1.SL.TZ1.S_4b:
Jim describes the correlation as very strong. Circle the value below which best represents the correlation coefficient.
-
18M.2.AHL.TZ1.H_6:
The mean number of squirrels in a certain area is known to be 3.2 squirrels per hectare of woodland. Within this area, there is a 56 hectare woodland nature reserve. It is known that there are currently at least 168 squirrels in this reserve.
Assuming the population of squirrels follow a Poisson distribution, calculate the probability that there are more than 190 squirrels in the reserve.
-
18M.1.SL.TZ1.T_4b:
Using the equation of the regression line, estimate the concentration of dissolved oxygen in the river when the temperature is 18 °C.
-
18M.1.SL.TZ2.T_12b.i:
Write down the total number of customers in terms of k.
-
16N.2.SL.TZ0.T_1a:
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the -axis and 2 cm to represent 10 points on the -axis.
-
17M.2.SL.TZ2.T_3e:
State a reason why the regression line on is appropriate to model the relationship between these variables.
-
16N.2.SL.TZ0.T_1e:
Write down the equation of the regression line on for these eight male students.
-
16N.2.SL.TZ0.T_1f:
Draw the regression line, from part (e), on your scatter diagram.
-
18M.3.AHL.TZ0.Hsp_4b.ii:
State your conclusion at the 1 % significance level.
-
17N.2.AHL.TZ0.H_2a:
Find .
-
19M.2.SL.TZ1.T_1d.ii:
Hence describe the correlation between temperature difference from 37 °C and heartbeat.
-
19M.1.SL.TZ1.S_9a:
Find P(−1.6 < < 2.4). Write your answer in terms of and .
-
19M.1.SL.TZ1.S_9c:
Write down the standardized value for .
-
18M.2.SL.TZ1.T_5a:
Write down the probability that Ayako avoids the trap in this wall.
-
18M.2.SL.TZ1.T_5b:
Find the probability that only one of Ayako and Natsuko falls into a trap while attempting to pass through a door in the first wall.
-
18N.1.SL.TZ0.S_9b.ii:
fourth draw.
-
19M.2.SL.TZ1.T_3e.i:
State the null hypothesis.
-
16N.2.SL.TZ0.S_7a:
Write down the probability that the first disc selected is red.
-
18M.2.SL.TZ2.T_2b.ii:
Use the cumulative frequency curve to find the lower quartile.
-
19M.2.SL.TZ2.T_1c.ii:
the statistic.
-
18M.2.SL.TZ2.S_1b:
Use your equation to estimate the mean weight of a child that is 1.95 years old.
-
18M.2.SL.TZ2.S_10a.i:
Write down the value of k.
-
18M.2.SL.TZ2.S_10b:
Find P(M < 95) .
-
18M.1.AHL.TZ1.H_3b:
Find the expected value of T.
-
19M.2.AHL.TZ2.H_2a:
Calculate the probability that, on a randomly selected day, Timmy makes a profit.
-
18N.2.AHL.TZ0.H_3b:
Find the probability that a randomly selected Infiglow battery will have a life of at least 15 hours.
-
17N.2.SL.TZ0.T_1a:
State whether is a discrete or a continuous variable.
-
17N.2.SL.TZ0.T_4e:
Find the probability that the liquid turns blue.
-
17M.1.SL.TZ2.T_11a:
Write down the probability that the mass of one of these corncobs is greater than 400 grams.
-
17M.1.SL.TZ1.T_1d:
Any trout with length 40 cm or less is returned to the lake.
Calculate the percentage of the fisherman’s catch that is returned to the lake.
-
18M.2.AHL.TZ2.H_8a:
Find the least possible value of n.
-
17N.1.SL.TZ0.T_1a.ii:
For the students in this group write down the median age.
-
17N.1.SL.TZ0.T_1b:
Draw a box-and-whisker diagram, for these students’ ages, on the following grid.

-
18M.2.SL.TZ1.S_9a:
Find the probability that an orange weighs between 289 g and 310 g.
-
18M.2.SL.TZ1.S_9d:
Find the probability that the grocer buys more than half the oranges in a box selected at random.
-
18M.2.SL.TZ2.S_10d.ii:
Find the probability that at least 48 bags in this crate contain at most one small apple.
-
18M.2.SL.TZ2.T_3a.i:
Find the probability that a basketball player has a weight that is less than 61 kg.
-
18M.2.SL.TZ2.T_3a.ii:
In a training session there are 40 basketball players.
Find the expected number of players with a weight less than 61 kg in this training session.
-
18M.2.SL.TZ2.T_3b.ii:
Find the value of q.
-
16N.1.AHL.TZ0.H_2a:
Complete the probability distribution table for .

-
17N.2.SL.TZ0.S_8d.ii:
Find the number of hives that have a high production.
-
16N.2.AHL.TZ0.H_1b:
Find the value of .
-
16N.2.AHL.TZ0.H_3b:
Given that and , use part (a) to find the value of .
-
17M.2.SL.TZ1.T_1f:
State whether it is valid to use the regression line to estimate the average weight of the brain of mice. Give a reason for your answer.
-
17M.2.SL.TZ1.S_9a:
Find .
-
17M.2.SL.TZ1.S_9d:
Given that , find .
-
16N.2.SL.TZ0.T_4b:
(i) Find the probability that a box of cereal, chosen at random, is sold.
(ii) Calculate the manufacturer’s expected daily income from these sales.
-
19N.1.SL.TZ0.S_2b:
Find the value of .
-
19N.2.SL.TZ0.S_7a:
Show that .
-
17M.1.SL.TZ1.T_4b:
Determine whether rock-climbing is offered by the school in the fall/autumn trimester.
-
18M.2.SL.TZ1.S_5b:
Given that P((A ∪ B)′ ) = 0.19, find P(A | B′ ).
-
18M.2.SL.TZ2.T_1b.iii:
Use the tree diagram to find the probability that an employee encountered traffic given that they were late for work.
-
18M.2.SL.TZ1.S_5a:
Find P(A ∩ B′ ).
-
17M.1.SL.TZ2.T_2d:
Write down the value of .
-
18M.2.AHL.TZ1.H_10c:
Given that , and that 0.25 < s < 0.4 , find the value of s.
-
17M.1.SL.TZ2.T_2c:
Find the number of children who play only football.
-
19M.2.AHL.TZ2.H_3c:
Find the probability that Iqbal passes his third paper, given that he passed only one previous paper.
-
17M.2.SL.TZ2.S_10a.ii:
Find .
-
19M.1.SL.TZ2.S_8b:
Find the value of the interquartile range.
-
19M.1.SL.TZ2.S_8a:
The range of the data is 16. Find the value of .
-
SPM.1.SL.TZ0.7a:
Find the median number of minutes spent traveling to work.
-
18M.1.AHL.TZ2.H_3b.ii:
Find P(X > μ).
-
20N.2.AHL.TZ0.H_9a:
Find the probability that a randomly selected packet has a weight less than .
-
20N.2.AHL.TZ0.H_9b:
The probability that a randomly selected packet has a weight greater than grams is . Find the value of .
-
20N.1.SL.TZ0.T_3b:
Use your graphic display calculator to find an estimate of the standard deviation of the weights of mangoes from this harvest.
-
20N.2.SL.TZ0.T_2a.i:
Find the value of .
-
20N.2.SL.TZ0.T_2a.ii:
Find the value of .
-
20N.2.SL.TZ0.T_6c.ii:
Find the probability that Emlyn plays more than in a game.
-
20N.2.SL.TZ0.T_6f:
Find the expected number of successful shots Emlyn will make on Monday, based on the results from Saturday and Sunday.
-
EXN.1.SL.TZ0.3:
The following table shows the probability distribution of a discrete random variable where .
Find the value of , justifying your answer.
-
EXN.2.SL.TZ0.4a.ii:
Interpret, in context, the value of found in part (a) (i).
-
EXN.2.AHL.TZ0.9:
A biased coin is weighted such that the probability, , of obtaining a tail is . The coin is tossed repeatedly and independently until a tail is obtained.
Let be the event “obtaining the first tail on an even numbered toss”.
Find .
-
21M.2.SL.TZ1.3c:
Given that a bag is not rejected, find the probability that it has a mass greater than grams.
-
21M.2.SL.TZ1.2a:
Write down the value of and the value of .
-
21M.2.SL.TZ1.2c:
Write down the value of and the value of .
-
21M.1.SL.TZ1.4b:
Hence, find the minimum possible value of .
-
21M.2.SL.TZ2.8a:
Given that of the flight times are longer than minutes, find the value of .
-
21M.2.SL.TZ2.9d:
The week is the first week in which the player is expected to make a profit. Ryan knows that if he buys a lottery ticket in the week, his expected profit is .
Find the value of .
-
21M.2.SL.TZ2.4d:
Determine if the events and are independent. Justify your answer.
-
21N.1.SL.TZ0.4b:
Let be the event that “box 1 is chosen” and let be the event that “a red ball is drawn”.
Determine whether events and are independent.
-
21N.2.SL.TZ0.1a:
Find Pearson’s product-moment correlation coefficient, , for these data.
-
21N.2.AHL.TZ0.1b:
The relationship between the variables can be modelled by the regression equation . Write down the value of and the value of .
-
21N.2.AHL.TZ0.1e:
Lucy suspected that each student had not been practising as much as they reported. In order to compensate for this, Lucy deducted a fixed number of hours per week from each of the students’ recorded hours.
State how, if at all, the value of would be affected.
-
22M.1.SL.TZ2.9b:
Find .
-
22M.2.SL.TZ2.5b:
Verify that the measurement of seconds is not an outlier.
-
22M.2.SL.TZ2.5c:
State why it appears that the mean reaction time is greater than the median reaction time.
-
22M.2.SL.TZ2.9a:
Find the value of .
-
22M.2.AHL.TZ2.8:
Rachel and Sophia are competing in a javelin-throwing competition.
The distances, metres, thrown by Rachel can be modelled by a normal distribution with mean and standard deviation .
The distances, metres, thrown by Sophia can be modelled by a normal distribution with mean and standard deviation .
In the first round of competition, each competitor must have five throws. To qualify for the next round of competition, a competitor must record at least one throw of metres or greater in the first round.
Find the probability that only one of Rachel or Sophia qualifies for the next round of competition.
-
22M.2.SL.TZ2.9d:
Given that Suzi will be late to work at least one day next week, find the probability that she will be late less than three times.
-
SPM.2.SL.TZ0.8b.ii:
Hence, find the probability that a seashell selected at random has a length greater than 26 mm.
-
SPM.2.SL.TZ0.8b.i:
Find , the standard deviation of X.
-
SPM.2.SL.TZ0.8d:
Find the probability that exactly three of these seashells have a length greater than 26 mm.
-
EXM.1.SL.TZ0.2c:
Give an example of a set of data with 7 numbers in it that does have an outlier, justify this fact by stating the Interquartile Range.
-
EXM.2.SL.TZ0.1b.ii:
Calculate the number of students in each grade in the sample.
-
EXM.2.SL.TZ0.1c:
State the name for this type of sampling technique.
-
18M.2.SL.TZ2.S_10c:
Find the probability that a bag of apples selected at random contains at most one small apple.
-
18M.1.SL.TZ1.T_2a:
Find the value of x.
-
18N.2.SL.TZ0.T_1a.ii:
Use your graphic display calculator to write down , the mean examination score.
-
18N.2.SL.TZ0.T_1c.ii:
Justify whether it is valid to use the regression line y on x to estimate Jerome’s examination score.
-
17M.2.SL.TZ2.S_8b.i:
Write down the coordinates of A.
-
17M.2.SL.TZ2.S_8b.ii:
Write down the rate of change of at A.
-
19M.1.SL.TZ1.T_5b:
Write down the probability that a bouquet of roses sold is not small.
-
19M.1.SL.TZ2.T_2c:
In order to estimate the amount of oxygen consumed, this regression line is considered to be reliable for a temperature such that ≤ ≤ .
Write down the value of and of .
-
19M.1.SL.TZ2.T_5c:
A student is chosen at random from the surveyed students.
Find the probability that this student likes kiwi fruit smoothies given that they like mango smoothies.
-
17N.1.AHL.TZ0.H_10a:
Show that the probability that Chloe wins the game is .
-
18N.1.AHL.TZ0.H_1a:
By drawing a Venn diagram, or otherwise, find .
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
18N.2.SL.TZ0.T_3c.i:
Write down the modal class.
-
18N.2.SL.TZ0.T_3d.ii:
Calculate an estimate of the standard deviation, giving your answer correct to three decimal places.
-
18M.3.AHL.TZ0.Hsp_4a:
State suitable hypotheses to investigate whether or not a negative linear association exists between X and Y.
-
18M.3.AHL.TZ0.Hsp_4b.i:
Determine the p-value.
-
19M.1.SL.TZ2.T_12a.ii:
.
-
19M.2.SL.TZ1.S_5b:
Use the model to predict how many edge pieces she had found when she had sorted a total of 750 pieces.
-
18M.1.SL.TZ2.T_12c:
Hence, complete the histogram.
-
17N.2.SL.TZ0.S_8a:
Write down the value of and of .
-
17M.2.SL.TZ2.T_3b.i:
Write down, for this set of data the mean number of folders produced, ;
-
18M.3.AHL.TZ0.Hsp_4c.ii:
Hence show that if U, V are independent random variables then the population product moment correlation coefficient, ρ, is zero.
-
17M.2.AHL.TZ1.H_1b:
Find .
-
19M.2.AHL.TZ2.H_10b:
Copy and complete the probability distribution table for Y.
-
19M.2.AHL.TZ2.H_10d:
In any given year of 365 days, the probability that Steffi does not visit Will for at most days in total is 0.5 (to one decimal place). Find the value of .
-
17N.1.SL.TZ0.T_5c:
By placing a tick (✔) in the correct box, determine which of the following statements is true:

-
19M.1.SL.TZ2.T_14a.ii:
Find the price that is two standard deviations above the mean price.
-
19M.2.SL.TZ1.T_3a:
Write down the total number of people, from this group, who are pet owners.
-
19M.2.SL.TZ1.T_3i:
State the conclusion for this test. Give a reason for your answer.
-
17M.1.SL.TZ1.S_1b:
A girl is selected at random. Find the probability that she takes economics but not history.
-
18M.2.SL.TZ2.T_2e:
Find the number of buses that travelled a distance less than or equal to 12 000 km.
-
17M.2.SL.TZ1.T_5a.ii:
Calculate the standard deviation.
-
17M.2.SL.TZ1.T_5b:
Find the median test grade of the students.
-
17M.2.SL.TZ1.T_5f.i:
Calculate the probability that a student chosen at random spent at least 90 minutes preparing for the test.
-
19M.2.SL.TZ2.T_1e.ii:
Find the probability that neither of the two students take the Spanish class.
-
18M.2.SL.TZ2.S_1a.ii:
Write down the correlation coefficient.
-
17N.2.SL.TZ0.S_8b:
Use this regression line to estimate the monthly honey production from a hive that has 270 bees.
-
17N.2.AHL.TZ0.H_4:
It is given that one in five cups of coffee contain more than 120 mg of caffeine.
It is also known that three in five cups contain more than 110 mg of caffeine.Assume that the caffeine content of coffee is modelled by a normal distribution.
Find the mean and standard deviation of the caffeine content of coffee. -
17N.2.SL.TZ0.T_1b.i:
Write down, for , the modal class;
-
17N.2.SL.TZ0.T_1c.i:
Use your graphic display calculator to estimate the mean of ;
-
17N.2.SL.TZ0.T_1g:
State the result of the test. Give a reason for your answer.
-
17M.1.SL.TZ2.S_3a:
Write down .
-
17M.1.SL.TZ1.T_7b:
Find the probability that Sara’s baggage arrives in London.
-
18M.2.AHL.TZ2.H_8b:
It is further given that P(X ≤ 1) = 0.09478 correct to 4 significant figures.
Determine the value of n and the value of p.
-
18M.2.AHL.TZ2.H_9a.i:
Find the probability that exactly 4 taxis arrive during T.
-
17N.1.SL.TZ0.T_13a:
Find the probability that this applicant took at least 40 minutes to complete the test.
-
18M.2.SL.TZ1.S_9b.i:
Find the standardized value for 289 g.
-
18M.2.SL.TZ1.S_9c:
To the nearest gram, find the minimum weight of an orange that the grocer will buy.
-
18M.2.SL.TZ1.T_2b:
Calculate the expected frequency of flights travelling at most 500 km and arriving slightly delayed.
-
18M.2.SL.TZ1.T_2c:
Write down the number of degrees of freedom.
-
17N.2.SL.TZ0.S_8e:
Adam decides to increase the number of bees in each low production hive. Research suggests that there is a probability of 0.75 that a low production hive becomes a regular production hive. Calculate the probability that 30 low production hives become regular production hives.
-
16N.2.AHL.TZ0.H_3a:
Show that .
-
16N.2.SL.TZ0.T_2d:
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.
-
17M.2.SL.TZ1.S_9b:
Find the value of .
-
16N.2.SL.TZ0.T_4a:
Draw a diagram that shows this information.
-
16N.1.SL.TZ0.T_2a:
Giving your answer to one decimal place, write down the value of
(i) the median level of Vitamin C content of the oranges in the sample;
(ii) the lower quartile;
(iii) the upper quartile.
-
19N.2.AHL.TZ0.H_7:
Runners in an athletics club have season’s best times for the 100 m, which can be modelled by a normal distribution with mean 11.6 seconds and standard deviation 0.8 seconds. To qualify for a particular competition a runner must have a season’s best time of under 11 seconds. A runner from this club who has qualified for the competition is selected at random. Find the probability that he has a season’s best time of under 10.7 seconds.
-
19N.1.SL.TZ0.S_7a:
Find so that .
-
19N.2.SL.TZ0.S_9a:
Calculate the probability a flight is not late.
-
17M.2.AHL.TZ2.H_1b:
Calculate the mean score.
-
16N.2.SL.TZ0.S_8c:
During week 3 each student spent 5% less time browsing the Internet than during week 1. For week 3, find
(i) the median;
(ii) the variance.
-
18M.1.SL.TZ2.S_8b:
Find the probability that Pablo leaves home before 07:00 and is late for work.
-
16N.1.SL.TZ0.T_3b:
On the Venn diagram, shade the region .
-
17M.2.AHL.TZ2.H_10c:
Find .
-
19M.1.SL.TZ1.S_1b:
Find the value of .
-
17M.1.AHL.TZ1.H_10a:
Find the value of .
-
17M.2.AHL.TZ2.H_10b:
Find .
-
18M.2.SL.TZ2.T_1b.ii:
Use the tree diagram to find the probability that an employee was late for work.
-
19M.2.AHL.TZ1.H_3b.i:
the mean.
-
17M.2.AHL.TZ2.H_10d:
Find the median of .
-
18M.1.SL.TZ2.T_9b.ii:
Shade, on the Venn diagram, the region represented by the set .
-
19M.2.AHL.TZ1.H_3a.ii:
Find the standard deviation.
-
18M.1.SL.TZ2.T_9a.ii:
Write down an expression, in set notation, for the shaded region represented by Diagram 2.
-
18M.2.SL.TZ2.T_1a.ii:
Write down the value of b.
-
SPM.1.SL.TZ0.7e.i:
Find the value of .
-
19M.1.SL.TZ2.S_8e.i:
the mean number of hours that the group of boys spent watching television.
-
19M.2.SL.TZ1.S_1b:
Find the value of .
-
SPM.1.SL.TZ0.7d:
Write down the value of .
-
20N.2.AHL.TZ0.H_9d:
From a random sample of packets, determine the number of packets that would be expected to have a weight lying within standard deviations of the mean.
-
20N.1.SL.TZ0.T_6b:
Find the probability that the second ball chosen is labelled , given that the first ball chosen was labelled .
-
EXN.2.SL.TZ0.8c:
Find the probability that a randomly chosen person will take more than minutes to complete the jigsaw puzzle.
-
EXN.2.SL.TZ0.4c:
Use the regression equation from part (b) to predict this patient’s systolic blood pressure.
-
21M.1.SL.TZ1.9c.i:
State the range of possible values of .
-
21M.1.SL.TZ1.9d:
Hence, find the range of possible values for .
-
21M.1.SL.TZ1.9a:
Find the value of .
-
21M.1.SL.TZ2.7b:
Given that of these Year 12 students spend more than hours per week doing homework, find the value of .
-
21M.1.SL.TZ2.7c:
Find the value of and the value of .
-
21M.2.SL.TZ2.1b:
Interpret, in context, the value of found in part (a)(i).
-
19M.2.SL.TZ1.T_1f:
Draw the regression line on on the scatter diagram.
-
21N.2.SL.TZ0.9a:
Find .
-
22M.2.SL.TZ2.5d:
Now consider the two box and whisker diagrams.
Comment on whether these box and whisker diagrams provide any evidence that might suggest that not sleeping well causes an increase in reaction time.
-
22M.2.SL.TZ2.9e:
Find the probability that Suzi will receive a bonus.
-
22M.1.SL.TZ1.3b.ii:
Find the mean age of all the adults surveyed.
-
SPM.2.AHL.TZ0.4c:
Jennifer was absent for the first test but scored 29 marks on the second test. Use an appropriate regression equation to estimate Jennifer’s mark on the first test.
-
EXM.2.SL.TZ0.1b.i:
Show that 3 students will be selected from grade 12.
-
EXM.1.SL.TZ0.2a:
Recalling definitions, such as the Lower Quartile is the piece of data with the data placed in order, find an expression for the Interquartile Range.
-
EXM.2.SL.TZ0.1e:
Another student at the school, Jasmine, has a self-esteem value of 29.
By finding the equation of an appropriate regression line, estimate the time Jasmine spent on social media the previous day.
-
EXM.1.SL.TZ0.2b:
Hence, show that a data set with only 5 numbers in it cannot have any outliers.
-
17M.2.SL.TZ1.S_1b.i:
Find the mean.
-
18M.1.SL.TZ1.T_6c.i:
Write down the mid-interval value for the 100 < x ≤ 150 group.
-
17M.2.SL.TZ2.S_8c.ii:
Find the the rate of change of at B.
-
19M.1.SL.TZ2.T_2b:
Draw the regression line of on on the scatter diagram.
-
19M.1.SL.TZ2.T_6b.ii:
Write down the approximate number of snacks whose amount of sugar ranges from 18 to 20 grams.
-
19M.1.SL.TZ2.T_6c:
The health inspector visits two school cafeterias. She inspects the same number of meals at each cafeteria. The data is shown in the following box-and-whisker diagrams.
Meals prepared in the school cafeterias are required to have less than 10 grams of sugar.
State, giving a reason, which school cafeteria has more meals that do not meet the requirement.
-
19M.1.SL.TZ2.T_5b:
Find the number of surveyed students who did not like any of the three flavours.
-
18N.1.SL.TZ0.T_8b:
Find the probability that Jorgé chooses a red disc.
-
18N.1.AHL.TZ0.H_1b:
Show that the events and are not independent.
-
18N.2.SL.TZ0.T_2b.i:
Write down .
-
19M.1.SL.TZ1.T_12c:
Write down the probability that the second spin is yellow, given that the first spin is blue.
-
17M.1.SL.TZ1.S_10a:
Show that .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
18N.2.SL.TZ0.T_3a.ii:
Find the interquartile range.
-
18N.2.SL.TZ0.T_3b:
Find the final examination result required to obtain the highest possible grade.
-
18M.2.SL.TZ1.S_8a:
Find the value of a and of b.
-
18M.2.AHL.TZ1.H_8:
Each of the 25 students in a class are asked how many pets they own. Two students own three pets and no students own more than three pets. The mean and standard deviation of the number of pets owned by students in the class are and respectively.
Find the number of students in the class who do not own a pet.
-
19M.2.SL.TZ1.S_5a:
Write down the value of and of .
-
17M.2.SL.TZ2.T_3a:
Draw a scatter diagram for this data. Use a scale of 2 cm for 5000 folders on the horizontal axis and 2 cm for 10 000 Euros on the vertical axis.
-
17N.2.AHL.TZ0.H_2b:
Find .
-
19M.2.SL.TZ1.T_1a:
Draw a scatter diagram for temperature difference from 37 °C () against heartbeat (). Use a scale of 2 cm for 0.1 °C on the horizontal axis, starting with −0.3 °C. Use a scale of 1 cm for 2 heartbeats per minute on the vertical axis, starting with 60 beats per minute.
-
19M.2.SL.TZ2.S_9c:
Find the value of .
-
19M.2.SL.TZ2.S_9d:
All flights have two pilots. Find the percentage of flights where both pilots flew more than 30 hours last week.
-
18M.1.SL.TZ2.T_7c:
Two girls are selected at random.
Calculate the probability that one girl answered questions in Mandarin and the other answered questions in Hindi.
-
18M.2.SL.TZ1.T_5d.i:
A contestant is chosen at random. Find the probability that this contestant fell into a trap while attempting to pass through a door in the second wall.
-
18N.1.SL.TZ0.S_9b.i:
third draw.
-
19M.2.SL.TZ1.S_10a.ii:
Find the probability of rolling two or more red faces.
-
19M.1.SL.TZ2.S_1b:
Find .
-
19M.1.AHL.TZ1.H_6b:
.
-
19M.2.SL.TZ1.T_3e.ii:
State the alternative hypothesis.
-
19M.2.SL.TZ1.T_3f:
Write down the number of degrees of freedom for this test.
-
17M.1.SL.TZ1.S_1a.i:
Find the value of ;
-
17M.1.SL.TZ1.S_1a.ii:
Find the value of .
-
18M.2.SL.TZ2.T_2d:
Write down the percentage of buses that travelled a distance greater than the upper quartile.
-
17M.2.SL.TZ1.T_5c:
Find the interquartile range.
-
19M.2.SL.TZ2.T_1b:
State the number of degrees of freedom.
-
17N.2.SL.TZ0.S_4b:
Write down .
-
18M.2.SL.TZ1.S_2b:
Calculate the expected value of the score.
-
17N.2.SL.TZ0.T_1b.ii:
Write down, for , the mid-interval value of the modal class.
-
17N.2.SL.TZ0.T_1e.ii:
Write down the number of degrees of freedom.
-
17M.2.AHL.TZ1.H_9a:
Find the probability that a runner selected at random will complete the marathon in less than 3 hours.
-
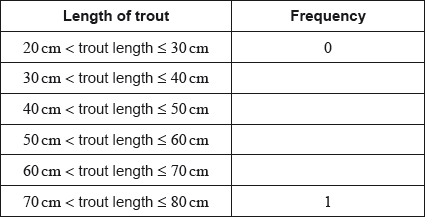
17M.1.SL.TZ1.T_1a:
Complete the following table.
-
18M.2.AHL.TZ2.H_9a.ii:
Find the most likely number of taxis that would arrive during T.
-
18M.2.AHL.TZ2.H_9b:
During quiet periods of the day, taxis arrive at a mean rate of 1.3 taxis every 10 minutes.
Find the probability that during a period of 15 minutes, of which the first 10 minutes is busy and the next 5 minutes is quiet, that exactly 2 taxis arrive.
-
18M.2.SL.TZ1.T_2d.i:
Write down the χ2 statistic.
-
18M.2.SL.TZ1.T_2d.ii:
Write down the associated p-value.
-
18M.2.SL.TZ2.T_3d.i:
For this test state the null hypothesis.
-
18M.2.SL.TZ2.T_3e:
State a conclusion for this test. Justify your answer.
-
17M.2.SL.TZ2.S_2b:
Use the regression equation to estimate the number of visitors on a day when the maximum temperature is 15 °C.
-
19N.2.AHL.TZ0.H_10b:
Sketch the graph of . State the coordinates of the end points and any local maximum or minimum points, giving your answers in terms of .
-
19N.2.SL.TZ0.S_1b:
Use your regression equation to predict the number of messages sent by a teenager that spent minutes talking on their phone in October.
-
19N.2.SL.TZ0.S_9c.ii:
Given that at least of these flights are on time, find the probability that exactly flights are on time.
-
19M.2.AHL.TZ1.H_9b.ii:
Find the probability that more than 100 cakes will be sold on a typical day.
-
17M.2.AHL.TZ2.H_1a:
One of the players is chosen at random. Find the probability that this player’s score was 5 or more.
-
19M.2.AHL.TZ1.H_9c.ii:
A female customer is selected at random. Find the probability that she buys a sandwich.
-
16N.2.SL.TZ0.S_8a:
Find the mean number of hours spent browsing the Internet.
-
17M.1.AHL.TZ1.H_10b.i:
By considering the graph of f write down the mean of ;
-
17M.1.AHL.TZ1.H_10b.ii:
By considering the graph of f write down the median of ;
-
18M.2.SL.TZ2.T_1b.i:
Use the tree diagram to find the probability that an employee encountered traffic and was late for work.
-
17M.1.AHL.TZ1.H_10b.iii:
By considering the graph of f write down the mode of .
-
18M.2.SL.TZ2.T_1a.i:
Write down the value of a.
-
19M.1.SL.TZ2.T_11b.ii:
Write down .
-
17N.1.SL.TZ0.S_1a:
Complete the following tree diagram.
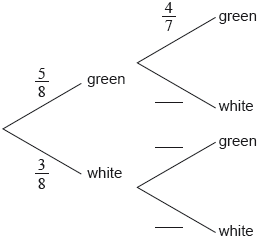
-
17M.1.SL.TZ1.T_4d:
Write down, in terms of , and , an expression for the set which contains only archery, baseball, kayaking and surfing.
-
19M.2.AHL.TZ1.H_3b.ii:
the standard deviation.
-
SPM.1.SL.TZ0.7c:
Find the value of .
-
19M.2.SL.TZ1.S_1a:
For these data, find the mean distance from a student’s home to school.
-
20N.1.AHL.TZ0.H_1:
A discrete random variable has the probability distribution given by the following table.
Given that , determine the value of and the value of .
-
20N.2.SL.TZ0.S_2a.i:
Find the value of and of .
-
20N.2.SL.TZ0.S_3a:
Find an expression for in terms of .
-
20N.2.SL.TZ0.S_3b.i:
Find the value of which gives the largest value of .
-
20N.1.SL.TZ0.T_14b:
Find the value of .
-
20N.1.SL.TZ0.T_3a:
Write down the modal group for these data.
-
20N.1.SL.TZ0.T_6a.ii:
Find the probability that the first ball chosen is labelled or labelled .
-
20N.1.SL.TZ0.T_7a:
Find the height of Flower null.
-
20N.2.SL.TZ0.T_2c:
Write down the value of .
-
20N.2.SL.TZ0.T_6c.i:
Find the probability that Emlyn plays between and in a game.
-
20N.2.SL.TZ0.T_6d:
Find the value of .
-
EXN.2.SL.TZ0.1:
A data set consisting of test scores has mean . One test score of requires a second marking and is removed from the data set.
Find the mean of the remaining test scores.
-
EXN.2.SL.TZ0.4d:
A ‐year‐old male patient enters the medical clinic for his appointment.
Explain why the regression equation from part (b) should not be used to predict this patient’s systolic blood pressure.
-
EXN.2.SL.TZ0.8e:
Having spent minutes attempting the jigsaw puzzle, a randomly chosen person had not yet completed the puzzle.
Find the probability that this person will take more than minutes to complete the jigsaw puzzle.
-
EXN.2.SL.TZ0.4a.i:
Determine the value of Pearson’s product‐moment correlation coefficient, , for these data.
-
21M.1.SL.TZ2.7d:
Estimate the number of Year 12 students that spend more than hours each week doing homework.
-
21M.1.SL.TZ2.7e.ii:
Suggest a more appropriate sampling method.
-
21M.2.SL.TZ2.8e:
Find the probability that more than of the flights on this particular day will have a flight time of more than minutes.
-
21M.2.AHL.TZ2.6a:
Show that .
-
21N.1.SL.TZ0.4a:
A box is chosen at random and a ball is drawn. Find the probability that the ball is red.
-
21N.2.SL.TZ0.4b:
Given that there is at least one defective lamp in the sample, find the probability that there are at most two defective lamps.
-
21N.2.AHL.TZ0.1d:
Lucy asserts that the number of hours a student practises has a direct effect on their final diploma result. Comment on the validity of Lucy’s assertion.
-
22M.1.AHL.TZ1.7a:
Find the value of .
-
22M.2.SL.TZ1.2a:
Find the value of .
-
22M.2.SL.TZ1.6b:
Find .
-
22M.2.SL.TZ1.9c.i:
Find the probability that the randomly selected muffin weighs less than .
-
22M.2.SL.TZ2.9b:
On a randomly selected day, find the probability that Suzi’s drive to work will take longer than minutes.
-
SPM.2.SL.TZ0.5b:
Let L2 be the regression line of y on x. The lines L1 and L2 pass through the same point with coordinates (p , q).
Find the value of p and the value of q.
-
17M.2.SL.TZ1.S_1a.i:
Write down the mode.
-
17M.2.SL.TZ1.S_1b.ii:
Find the variance.
-
18M.1.SL.TZ1.T_2b.i:
Find the standard deviation
-
18M.1.SL.TZ1.T_6b:
Complete the table.
-
18N.2.SL.TZ0.T_1c.i:
Use the regression line y on x to estimate Jerome’s examination score.
-
17M.2.SL.TZ2.S_8a:
Find the value of .
-
19M.1.SL.TZ1.T_2d.i:
For these eight animals find the mean speed.
-
19M.1.SL.TZ1.T_5a:
Complete the cumulative frequency table.
-
18N.2.SL.TZ0.T_2c.iii:
Find the probability that this student is taught in Spanish, given that the student studies Biology.
-
17M.1.SL.TZ1.S_4c:
Jim’s model is , for . Use his model to predict the decrease in temperature for any 2 minute interval.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
17M.1.SL.TZ2.T_6b:
Write down the number of leaves with a length less than or equal to 8 cm.
-
16N.1.SL.TZ0.T_12a:
Complete the tree diagram below.
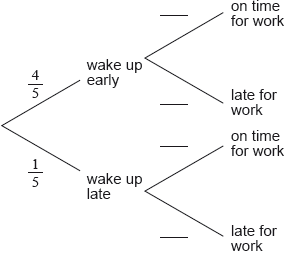
-
19M.1.SL.TZ2.T_12a.i:
.
-
18M.1.SL.TZ1.T_4a.ii:
For these data, find the equation of the regression line y on x.
-
18M.2.SL.TZ2.S_1a.i:
Find the value of a and of b.
-
17M.2.SL.TZ2.T_3f:
Use your graphic display calculator to find the equation of the regression line on .
-
16N.1.AHL.TZ0.H_10a:
Show that .
-
17M.2.AHL.TZ1.H_1a:
Calculate ;
-
19M.2.SL.TZ1.T_1d.i:
Use your graphic display calculator to find the Pearson’s product–moment correlation coefficient, .
-
18N.1.SL.TZ0.S_9a.i:
Find the probability, in terms of , that the game will end on her first draw.
-
19M.1.AHL.TZ1.H_6a:
.
-
19M.2.SL.TZ1.T_3c.iii:
For these data, write down the upper quartile.
-
19M.2.SL.TZ1.T_3d:
Write down the ratio of teenagers to non-teenagers in its simplest form.
-
17M.1.SL.TZ2.T_7a:
Write down an equation, in terms of and , for the total number of times the die was rolled.
-
17M.1.SL.TZ2.T_7b:
Using the mean score, write down a second equation in terms of and .
-
19M.2.SL.TZ2.T_1c.i:
the expected frequency of female students who chose to take the Chinese class.
-
18N.2.SL.TZ0.S_9b:
The probability that the reaction time of a person in Group Y is greater than 0.65 seconds is 0.396. Find the value of σ.
-
18N.2.AHL.TZ0.H_3a:
Find the value of and the value of .
-
19M.1.SL.TZ1.T_11b:
Find the probability that a suitcase weighs less than 15 kg.
-
17N.2.SL.TZ0.T_1d:
Find the expected frequency of students choosing the Science category and obtaining 31 to 40 correct answers.
-
17N.2.SL.TZ0.T_1e.i:
Write down the null hypothesis for this test;
-
17N.2.SL.TZ0.T_1f.i:
Write down the -value for the test;
-
17N.2.SL.TZ0.T_4f:
Find the probability that the tested adult is allergic to nuts given that the liquid turned blue.
-
17M.1.SL.TZ2.S_8a.i:
Find the median number of hours worked by the employees.
-
17M.1.SL.TZ2.S_8c:
Find the number of employees who earned £200 or less.
-
17M.1.SL.TZ2.S_8d:
Only 10 employees earned more than £. Find the value of .
-
17N.1.SL.TZ0.T_1a.i:
For the students in this group find the mean age;
-
18N.2.SL.TZ0.S_9d:
Ten of the participants with reaction times greater than 0.65 are selected at random. Find the probability that at least two of them are in Group X.
-
18M.2.SL.TZ1.S_9b.ii:
Hence, find the value of σ.
-
18M.2.SL.TZ2.S_10d.i:
Find the expected number of bags in this crate that contain at most one small apple.
-
18M.2.AHL.TZ1.H_4a:
Find the probability that a wolf selected at random is at least 5 years old.
-
16N.2.SL.TZ0.T_2b:
Show that .
-
16N.2.SL.TZ0.T_2c:
Write down the value of .
-
17M.2.SL.TZ1.S_9c:
Find .
-
19N.3.AHL.TZ0.Hsp_1a.ii:
Carry out a suitable test at the 5 % significance level. With reference to the -value, state your conclusion in the context of Peter’s claim.
-
19N.3.AHL.TZ0.Hsp_1b:
Peter uses the regression line of on as and calculates that a student with a Mathematics test score of 73 will have a running time of 101 seconds. Comment on the validity of his calculation.
-
19N.1.SL.TZ0.S_2a:
Write down the value of .
-
19N.1.SL.TZ0.S_7b:
It is given that .
Find .
-
19N.2.SL.TZ0.S_9d:
SpeedWay increases the number of flights from city to city to flights each week, and improves their efficiency so that more flights are on time. The probability that at least flights are on time is .
A flight is chosen at random. Calculate the probability that it is on time.
-
19M.2.AHL.TZ1.H_9a.i:
both a sandwich and a cake.
-
16N.2.AHL.TZ0.H_11e:
Determine the minimum value of such that the probability Kati receives at least one free gift is greater than 0.5.
-
17M.2.SL.TZ1.S_4b.ii:
Hence, find the probability that fewer than students are left handed.
-
19M.1.SL.TZ1.T_7a:
Place the numbers and in the correct position on the Venn diagram.
-
17M.1.AHL.TZ1.H_10c.i:
Show that .
-
18M.1.SL.TZ2.S_8d:
Given that Pablo is late for work, find the probability that he left home before 07:00.
-
19M.1.SL.TZ2.T_11b.i:
Write down the elements that belong to .
-
18M.1.SL.TZ2.T_9a.iii:
Write down an expression, in set notation, for the shaded region represented by Diagram 3.
-
17M.1.SL.TZ1.T_4c.i:
Write down the elements of the set ;
-
SPM.1.SL.TZ0.7b:
Find the number of employees whose travelling time is within 15 minutes of the median.
-
17M.2.SL.TZ1.S_4a:
Find .
-
16N.1.SL.TZ0.S_5b:
Find .
-
19M.1.SL.TZ2.S_8c:
Find the mean number of hours that the girls in this group spent watching television that week.
-
SPM.1.SL.TZ0.7e.ii:
Hence, find the interquartile range.
-
19M.2.SL.TZ1.S_1c:
Find the interquartile range.
-
19M.2.AHL.TZ1.H_3a.i:
Find the mean.
-
20N.2.AHL.TZ0.H_9e:
Packets are delivered to supermarkets in batches of . Determine the probability that at least packets from a randomly selected batch have a weight less than .
-
20N.1.SL.TZ0.S_1a.ii:
Find the value of .
-
20N.1.SL.TZ0.S_1b:
Find the probability that a randomly selected student from the class plays tennis or volleyball, but not both.
-
20N.1.SL.TZ0.S_8b:
Write down the value of the median distance in kilometres (km).
-
20N.1.SL.TZ0.T_14a:
Complete the values in the tree diagram.
-
20N.1.SL.TZ0.T_14c:
Given that Andre did not become the champion, find the probability that he lost in the semi-final.
-
20N.1.SL.TZ0.T_7d.ii:
Using your answers to parts (b) and (c), find the height of Flower .
-
20N.2.SL.TZ0.T_6g:
Emlyn claims the results from Saturday and Sunday show that his expected number of successful shots will be more than Johan’s.
Determine if Emlyn’s claim is correct. Justify your reasoning.
-
EXN.2.SL.TZ0.8d:
Find the probability that at least five of them will take more than minutes to complete the jigsaw puzzle.
-
21M.1.SL.TZ1.9e:
Agnes and Barbara play a game using these dice. Agnes rolls die once and Barbara rolls die once. The probability that Agnes’ score is less than Barbara’s score is .
Find the value of .
-
21M.1.SL.TZ1.9b:
Hence, find the value of .
-
21M.2.SL.TZ2.8b:
Find the probability that a randomly selected flight will have a flight time of more than minutes.
-
21M.2.SL.TZ2.9c:
Given that the grand prize is not won and the grand prize continues to double, write an expression in terms of for the value of the grand prize in the week of the lottery.
-
21M.2.SL.TZ2.1a.ii:
Write down the value of Pearson’s product-moment correlation coefficient, .
-
18M.2.SL.TZ2.T_2g:
The smallest distance travelled by one of the buses was 2500 km.
The longest distance travelled by one of the buses was 23 000 km.On graph paper, draw a box-and-whisker diagram for these data. Use a scale of 2 cm to represent 5000 km.
-
21N.2.SL.TZ0.9c.i:
medium.
-
21N.2.AHL.TZ0.1a:
Find Pearson’s product-moment correlation coefficient, , for these data.
-
22M.1.AHL.TZ1.7b:
Find .
-
22M.2.SL.TZ1.9a:
Find the probability that a randomly selected chocolate muffin weighs less than .
-
22M.2.SL.TZ1.9d:
Find the value of .
-
22M.2.SL.TZ1.9b:
In a random selection of chocolate muffins, find the probability that exactly weigh less than .
-
SPM.2.SL.TZ0.8c:
Find E(Y).
-
SPM.2.SL.TZ0.8a:
Find P(24.15 < X < 25).
-
SPM.2.AHL.TZ0.6b:
Given that Var(X) = 0.8419, find Var(T).
-
SPM.2.SL.TZ0.4b:
The die is tossed five times. Find the probability of obtaining the third “six” on the fifth toss.
-
EXM.2.SL.TZ0.1d.ii:
Interpret the meaning of the value of in the context of the principal’s concerns.
-
18M.1.SL.TZ1.T_6a:
Write down the median.
-
18N.2.SL.TZ0.T_1a.iii:
Use your graphic display calculator to write down r , Pearson’s product–moment correlation coefficient.
-
17M.2.SL.TZ2.S_8d:
Let be the region enclosed by the graph of , the -axis, the line and the line . The region is rotated 360° about the -axis. Find the volume of the solid formed.
-
18N.1.SL.TZ0.T_2a:
Write down the modal length of the rods.
-
17N.1.AHL.TZ0.H_10b.ii:
Determine the variance of X.
-
18N.1.SL.TZ0.T_2b:
Find the median length of the rods.
-
18N.2.SL.TZ0.S_1a:
Write down the number of students in the group who take art class.
-
19M.1.SL.TZ1.T_12b:
Find the probability that at least one of the spins is yellow.
-
19M.2.SL.TZ2.S_1a.i:
Write down the value of and of .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
18M.1.SL.TZ2.S_3b.ii:
Find the value of the new variance.
-
18N.2.SL.TZ0.T_3c.ii:
Write down the mid-interval value of the modal class.
-
17M.1.SL.TZ2.T_10c:
Write down an expression, in terms of , for the probability that at least one of Deborah’s three light bulbs is defective.
-
18M.2.SL.TZ1.S_8c:
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
-
18M.1.SL.TZ2.T_12b.ii:
Calculate the value of k.
-
17M.2.SL.TZ1.T_1a:
Find the range of the average body weights for these seven species of mammal.
-
17M.2.SL.TZ2.T_3c:
Label the point on the scatter diagram.
-
17M.2.SL.TZ2.T_3d:
Use your graphic display calculator to find the Pearson’s product–moment correlation coefficient, .
-
18M.1.SL.TZ2.T_1a:
Plot and label the point M on the scatter diagram.
-
18M.3.AHL.TZ0.Hsp_4c.i:
Show that Cov(U, V) = E(UV) − E(U)E(V).
-
19M.2.SL.TZ1.T_1b.i:
Write down, for this set of data the mean temperature difference from 37 °C, .
-
19M.2.SL.TZ1.T_1b.ii:
Write down, for this set of data the mean number of heartbeats per minute, .
-
19M.2.AHL.TZ2.H_10a:
Find the probability that on a randomly selected day, Steffi does not visit Will’s house.
-
19M.2.AHL.TZ2.H_10c:
Hence find the expected number of times per day that Steffi is fed at Will’s house.
-
18M.1.SL.TZ2.T_7b:
Find the probability that the boy answered questions in Hindi.
-
17N.1.SL.TZ0.T_5b:
Draw the regression line on the scatter diagram.
-
18M.2.SL.TZ1.T_5d.ii:
A contestant is chosen at random. Find the probability that this contestant fell into a trap.
-
18N.2.SL.TZ0.S_2a.i:
Find the value of a and of b.
-
19M.2.SL.TZ1.T_3c.i:
For these data, write down the median number of pets.
-
19M.2.SL.TZ1.T_3c.ii:
For these data, write down the lower quartile.
-
17M.1.SL.TZ2.T_7c:
Find the value of and of .
-
18M.2.SL.TZ2.T_2b.iii:
Use the cumulative frequency curve to find the upper quartile.
-
17M.2.SL.TZ1.T_5a.i:
Calculate the mean test grade of the students;
-
19M.2.SL.TZ2.T_1e.iii:
Find the probability that at least one of the two students is female.
-
18M.2.SL.TZ2.S_10a.ii:
Show that μ = 106.
-
17N.2.SL.TZ0.S_4a:
Find the value of .
-
19M.2.AHL.TZ2.H_2b:
The shop is open for 24 days every month.
Calculate the probability that, in a randomly selected month, Timmy makes a profit on between 5 and 10 days (inclusive).
-
19M.1.SL.TZ1.T_11c:
Any suitcase that weighs more than kg is identified as excess baggage.
19.6 % of the suitcases at this airport are identified as excess baggage.Find the value of .
-
18M.1.SL.TZ1.T_13b:
A second school, Mulberry Park, also opens at 08:00 every morning. The arrival times of the students at this school follows exactly the same distribution as Malthouse school.
Given that, on one morning, 15 students arrive at least 60 minutes after the school opens, estimate the number of students at Mulberry Park school.
-
17N.2.SL.TZ0.T_4c:
Copy and complete the tree diagram.
-
17N.2.SL.TZ0.T_4d:
Find the probability that this adult is allergic to nuts and the liquid turns blue.
-
17M.1.SL.TZ2.S_3b:
Find .
-
17M.1.SL.TZ2.S_8b.i:
Find the amount of money an employee earned for working 40 hours;
-
17M.1.SL.TZ2.T_11b:
Find the value of .
-
17M.2.AHL.TZ1.H_9c:
Find the standard deviation of the times taken by female runners.
-
17M.2.AHL.TZ2.H_3a:
Given that and find the probability that a randomly chosen packet of biscuits is underweight.
-
17M.2.AHL.TZ2.H_3b:
Calculate the new value of giving your answer correct to two decimal places.
-
17M.1.SL.TZ1.T_2c:
Write down your answer to part (b) in the form where and k .
-
17M.1.SL.TZ1.T_7a:
Complete the tree diagram.
-
18M.2.AHL.TZ2.H_9a.iii:
Given that more than 5 taxis arrive during T, find the probability that exactly 7 taxis arrive during T.
-
17N.1.SL.TZ0.T_13b:
Find the value of .
-
17N.1.SL.TZ0.T_13c:
Estimate the number of applicants who completed the test in less than 25 minutes.
-
18N.2.SL.TZ0.S_9c:
A randomly selected participant has a reaction time greater than 0.65 seconds. Find the probability that the participant is in Group X.
-
18M.2.AHL.TZ2.H_3a:
Sketch the probability density function for X, and shade the region representing P(μ − 2σ < X < μ + σ).
-
18M.2.AHL.TZ2.H_3b:
Find the value of P(μ − 2σ < X < μ + σ).
-
16N.1.AHL.TZ0.H_2b:
Find the expected value of .
-
17M.2.SL.TZ1.T_1b.ii:
For the data from these seven species describe the correlation between the average body weight and the average weight of the brain.
-
16N.1.SL.TZ0.T_2b:
Draw a box-and-whisker diagram on the grid below to represent the Vitamin C content, in milligrams, for this sample.

-
19N.3.AHL.TZ0.Hsp_1a.i:
State suitable hypotheses and to test Peter’s claim, using a two-tailed test.
-
19N.2.AHL.TZ0.H_10c.ii:
.
-
19N.2.AHL.TZ0.H_10c.iii:
the median of .
-
19N.1.SL.TZ0.S_2c:
Write down the value of and of .
-
16N.2.AHL.TZ0.H_11b:
Find the values of the constants and .
-
18M.1.SL.TZ1.T_10b:
Find the value of x.
-
17M.1.SL.TZ2.T_2b:
Complete the Venn diagram using the above information.
-
18M.1.SL.TZ2.S_8a:
Copy and complete the following tree diagram.
-
18M.2.AHL.TZ1.H_10b:
Find .
-
19M.2.AHL.TZ2.H_3b:
Calculate the probability that Iqbal passes at least two of the papers he attempts.
-
17M.1.SL.TZ1.T_4c.ii:
Write down .
-
19M.2.AHL.TZ1.H_3c:
A ninth student also takes the test.
Explain why the median is unchanged.
-
19M.1.SL.TZ2.S_8d.ii:
Find the mean number of hours that all 30 girls and boys spent watching television that week.
-
19M.1.SL.TZ2.S_8d.i:
Find the total number of hours the group of boys spent watching television that week.
-
20N.2.SL.TZ0.S_3b.ii:
Hence, find the largest value of .
-
20N.2.SL.TZ0.S_9b:
Find .
-
20N.2.SL.TZ0.S_9e:
This year, Fiona will go to school on days.
Calculate the number of days Fiona is expected to arrive on time.
-
20N.1.SL.TZ0.T_6a.i:
Find the probability that the first ball chosen is labelled .
-
EXN.2.SL.TZ0.4b:
Find the equation of the regression line of on .
-
21M.2.SL.TZ1.3b:
Estimate the number of bags which will be rejected from a random sample of bags.
-
21M.2.SL.TZ2.1c:
On another day, Sarah visits the café to order a coffee. Seven customers have already ordered their coffee and are waiting to receive it.
Use the result from part (a)(i) to estimate Sarah’s waiting time to receive her coffee.
-
21M.2.SL.TZ2.4a:
Find the probability that the student plays a sport and is involved in theatre.
-
21N.2.SL.TZ0.1c:
One of these eight students was disappointed with her result and wished she had practised more. Based on the given data, determine how her score could have been expected to alter had she practised an extra five hours per week.
-
22M.2.SL.TZ1.4a:
Show that .
-
22M.2.SL.TZ2.5a:
State the median reaction time after sleeping well.
-
EXM.2.SL.TZ0.1a:
State the name for this type of sampling technique.
-
SPM.1.SL.TZ0.2:
Let A and B be events such that , and .
Find .
-
18M.1.SL.TZ1.T_2b.ii:
Find the interquartile range.
-
18N.2.SL.TZ0.T_1b.i:
Find the exact value of m and of c for these data.
-
19M.1.SL.TZ1.T_5c:
A customer buys a large bouquet.
Find the probability that there are 12 roses in this bouquet.
-
18N.1.SL.TZ0.T_2c.ii:
Calculate the interquartile range.
-
18N.2.SL.TZ0.T_2a.i:
Find the number of students in the school that are taught in Spanish.
-
18N.2.SL.TZ0.T_2a.ii:
Find the number of students in the school that study Mathematics in English.
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
18N.2.SL.TZ0.T_3e:
The teacher sets a grade boundary that is one standard deviation below the mean.
Use the cumulative frequency graph to estimate the number of students whose final examination result was below this grade boundary.
-
19M.2.SL.TZ1.S_3b:
The graph of has a horizontal tangent line at and at . Find .
-
17M.1.SL.TZ2.T_6a:
Write down the median length of these leaves.
-
17M.1.SL.TZ2.T_6c.ii:
Before measuring, the researcher estimated to be approximately 9.5 cm. Find the percentage error in her estimate.
-
17M.1.SL.TZ2.T_10a:
Write down the probability that a light bulb produced by Home Shine is not defective.
-
19M.1.SL.TZ2.T_12c:
Use the cumulative frequency curve to find an estimate for the number of students who worked at most 35 hours per month.
-
18M.1.SL.TZ2.T_12a:
Write down the mid-interval value for 10 ≤ t < 15.
-
16N.2.SL.TZ0.T_1d:
Write down the value of , the Pearson’s product–moment correlation coefficient, for these data.
-
17M.2.SL.TZ2.T_3b.ii:
Write down, for this set of data the mean production cost, .
-
17N.2.AHL.TZ0.H_2c:
Hence show that events and are independent.
-
17N.1.SL.TZ0.T_5d:
Diogo is 18 years old. Give a reason why the regression line should not be used to estimate the number of hours Diogo watches television per week.
-
18N.1.SL.TZ0.S_9c:
Hayley plays the game when = 5. She pays $20 to play and can earn money back depending on the number of draws it takes to obtain a blue marble. She earns no money back if she obtains a blue marble on her first draw. Let M be the amount of money that she earns back playing the game. This information is shown in the following table.
Find the value of so that this is a fair game.
-
19M.2.SL.TZ1.S_10a.i:
Find the probability of rolling exactly one red face.
-
19M.2.SL.TZ1.S_10b:
Show that, after a turn, the probability that Ted adds exactly $10 to his winnings is .
-
19M.2.SL.TZ1.S_10c.i:
Write down the value of .
-
19M.2.SL.TZ1.S_10d:
Ted will always have another turn if he expects an increase to his winnings.
Find the least value of for which Ted should end the game instead of having another turn.
-
18N.2.SL.TZ0.S_2a.ii:
Write down the correlation coefficient.
-
19M.1.SL.TZ2.T_14b:
Find the probability that the price of a kilogram of tomatoes, chosen at random, will be between 2.00 and 3.00 euro.
-
16N.2.SL.TZ0.S_7b:
Let be the number of red discs selected. Find the smallest value of for which .
-
17M.2.SL.TZ1.T_5f.ii:
Calculate the expected number of students that spent at least 90 minutes preparing for the test.
-
18M.1.AHL.TZ1.H_3a:
Find the value of a and the value of b.
-
17N.2.SL.TZ0.S_4c:
Find .
-
18M.2.SL.TZ1.S_2a:
Find the value of k.
-
17N.2.SL.TZ0.T_1c.ii:
Use your graphic display calculator to estimate the standard deviation of .
-
17N.2.SL.TZ0.T_1f.ii:
Write down the statistic.
-
17M.1.SL.TZ2.S_8a.ii:
Write down the number of employees who worked 50 hours or less.
-
17M.1.SL.TZ2.S_8b.ii:
Find the amount of money an employee earned for working 43 hours.
-
17M.1.SL.TZ1.T_1b:
State whether length of trout is a continuous or discrete variable.
-
18M.2.SL.TZ1.T_2f:
Write down the probability that this flight arrived on time.
-
18M.2.SL.TZ1.T_2g:
Given that this flight was not heavily delayed, find the probability that it travelled between 500 km and 5000 km.
-
17N.2.SL.TZ0.S_8c:
Write down the number of low production hives.
-
16N.2.AHL.TZ0.H_1a:
Determine the value of .
-
17M.2.SL.TZ2.S_2a.i:
Find the value of and of .
-
17M.2.SL.TZ2.S_2a.ii:
Write down the value of .
-
19N.2.AHL.TZ0.H_10c.i:
.
-
19N.2.SL.TZ0.S_9b:
Find the value of .
-
19N.2.SL.TZ0.S_9c.i:
Calculate the probability that at least of these flights are on time.
-
19M.2.AHL.TZ1.H_9c.i:
A customer is selected at random. Find the probability that the customer is male and buys a sandwich.
-
19M.1.AHL.TZ2.H_10a:
State the mode of .
-
19M.1.AHL.TZ2.H_10c.ii:
.
-
19M.1.AHL.TZ2.H_10b.i:
Find .
-
19M.1.AHL.TZ2.H_10b.ii:
Hence show that .
-
19M.2.AHL.TZ1.H_9a.ii:
only a sandwich.
-
16N.2.AHL.TZ0.H_11d:
(i) Hence show that has two modes and .
(ii) State the values of and .
-
19M.1.SL.TZ1.T_7b:
In the table indicate which two of the given statements are true by placing a tick (✔) in the right hand column.
-
19M.1.SL.TZ2.T_11a:
Write down the elements that belong to .
-
18M.2.SL.TZ2.T_1c.i:
Find the value of x.
-
17M.1.SL.TZ2.T_2a:
Write down an expression, in terms of , for the number of children who play only basketball.
-
17M.2.AHL.TZ2.H_10f:
Find .
-
17M.2.SL.TZ1.S_4b.i:
Hence, find the probability that exactly students are left handed;
-
17M.2.SL.TZ2.S_10b.iii:
The bag contains a total of ten marbles of which are white. Find .
-
17N.1.SL.TZ0.S_1b:
Find the probability that exactly one of the selected balls is green.
-
17M.2.SL.TZ2.S_10b.i:
Write down the probability of drawing three blue marbles.
-
16N.1.SL.TZ0.T_3a:
In the table indicate whether the given statements are True or False.
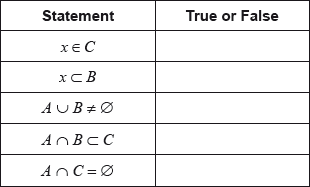
-
17M.2.SL.TZ2.S_10c:
Jill plays the game nine times. Find the probability that she wins exactly two prizes.
-
18M.1.AHL.TZ2.H_3a:
Find the value of p.
Sub sections and their related questions
SL 4.1—Concepts, reliability and sampling techniques
-
EXM.1.SL.TZ0.2a:
Recalling definitions, such as the Lower Quartile is the piece of data with the data placed in order, find an expression for the Interquartile Range.
-
EXM.1.SL.TZ0.2b:
Hence, show that a data set with only 5 numbers in it cannot have any outliers.
-
EXM.1.SL.TZ0.2c:
Give an example of a set of data with 7 numbers in it that does have an outlier, justify this fact by stating the Interquartile Range.
-
EXM.2.SL.TZ0.1a:
State the name for this type of sampling technique.
-
EXM.2.SL.TZ0.1b.i:
Show that 3 students will be selected from grade 12.
-
EXM.2.SL.TZ0.1b.ii:
Calculate the number of students in each grade in the sample.
-
EXM.2.SL.TZ0.1c:
State the name for this type of sampling technique.
-
EXM.2.SL.TZ0.1d.i:
Calculate Pearson’s product moment correlation coefficient, .
-
EXM.2.SL.TZ0.1d.ii:
Interpret the meaning of the value of in the context of the principal’s concerns.
-
EXM.2.SL.TZ0.1d.iii:
Explain why the value of makes it appropriate to find the equation of a regression line.
-
EXM.2.SL.TZ0.1e:
Another student at the school, Jasmine, has a self-esteem value of 29.
By finding the equation of an appropriate regression line, estimate the time Jasmine spent on social media the previous day.
-
17M.2.SL.TZ2.S_8a:
Find the value of .
-
17M.2.SL.TZ2.S_8b.i:
Write down the coordinates of A.
-
17M.2.SL.TZ2.S_8b.ii:
Write down the rate of change of at A.
-
17M.2.SL.TZ2.S_8c.i:
Find the coordinates of B.
-
17M.2.SL.TZ2.S_8c.ii:
Find the the rate of change of at B.
-
17M.2.SL.TZ2.S_8d:
Let be the region enclosed by the graph of , the -axis, the line and the line . The region is rotated 360° about the -axis. Find the volume of the solid formed.
-
18M.1.SL.TZ1.S_2a:
Find the value of the interquartile range.
-
18M.1.SL.TZ1.S_2b:
One student sent k text messages, where k > 11 . Given that k is an outlier, find the least value of k.
-
17M.2.SL.TZ1.S_1a.i:
Write down the mode.
-
17M.2.SL.TZ1.S_1a.ii:
Find the value of the range.
-
17M.2.SL.TZ1.S_1b.i:
Find the mean.
-
17M.2.SL.TZ1.S_1b.ii:
Find the variance.
-
19M.2.SL.TZ1.S_3b:
The graph of has a horizontal tangent line at and at . Find .
-
21M.1.SL.TZ1.4a:
Find the minimum possible value of .
-
21M.1.SL.TZ1.4b:
Hence, find the minimum possible value of .
-
21M.1.SL.TZ2.7e.i:
Explain why this sampling method might not provide an accurate representation of the amount of time all of the students in the school spend doing homework.
-
21M.1.SL.TZ2.7e.ii:
Suggest a more appropriate sampling method.
-
22M.1.SL.TZ1.3a:
Find the largest value of that would not be considered an outlier.
-
22M.2.SL.TZ2.5b:
Verify that the measurement of seconds is not an outlier.
SL 4.2—Histograms, CF graphs, box plots
-
SPM.1.SL.TZ0.7a:
Find the median number of minutes spent traveling to work.
-
SPM.1.SL.TZ0.7b:
Find the number of employees whose travelling time is within 15 minutes of the median.
-
SPM.1.SL.TZ0.7c:
Find the value of .
-
SPM.1.SL.TZ0.7d:
Write down the value of .
-
SPM.1.SL.TZ0.7e.i:
Find the value of .
-
SPM.1.SL.TZ0.7e.ii:
Hence, find the interquartile range.
-
SPM.1.SL.TZ0.7f:
Travelling times of less than minutes are considered outliers.
Find the value of .
-
17M.1.SL.TZ2.T_6a:
Write down the median length of these leaves.
-
17M.1.SL.TZ2.T_6b:
Write down the number of leaves with a length less than or equal to 8 cm.
-
17M.1.SL.TZ2.T_6c.i:
Use the graph to find the value of .
-
17M.1.SL.TZ2.T_6c.ii:
Before measuring, the researcher estimated to be approximately 9.5 cm. Find the percentage error in her estimate.
-
17M.1.SL.TZ2.S_8a.i:
Find the median number of hours worked by the employees.
-
17M.1.SL.TZ2.S_8a.ii:
Write down the number of employees who worked 50 hours or less.
-
17M.1.SL.TZ2.S_8b.i:
Find the amount of money an employee earned for working 40 hours;
-
17M.1.SL.TZ2.S_8b.ii:
Find the amount of money an employee earned for working 43 hours.
-
17M.1.SL.TZ2.S_8c:
Find the number of employees who earned £200 or less.
-
17M.1.SL.TZ2.S_8d:
Only 10 employees earned more than £. Find the value of .
-
17N.2.SL.TZ0.S_8a:
Write down the value of and of .
-
17N.2.SL.TZ0.S_8b:
Use this regression line to estimate the monthly honey production from a hive that has 270 bees.
-
17N.2.SL.TZ0.S_8c:
Write down the number of low production hives.
-
17N.2.SL.TZ0.S_8d.i:
Find the value of ;
-
17N.2.SL.TZ0.S_8d.ii:
Find the number of hives that have a high production.
-
17N.2.SL.TZ0.S_8e:
Adam decides to increase the number of bees in each low production hive. Research suggests that there is a probability of 0.75 that a low production hive becomes a regular production hive. Calculate the probability that 30 low production hives become regular production hives.
-
17M.1.SL.TZ1.T_1a:
Complete the following table.

-
17M.1.SL.TZ1.T_1b:
State whether length of trout is a continuous or discrete variable.
-
17M.1.SL.TZ1.T_1c:
Write down the modal class.
-
17M.1.SL.TZ1.T_1d:
Any trout with length 40 cm or less is returned to the lake.
Calculate the percentage of the fisherman’s catch that is returned to the lake.
-
19M.1.SL.TZ1.T_2a:
State whether speed is a continuous or discrete variable.
-
19M.1.SL.TZ1.T_2b:
Write down the median speed for these animals.
-
19M.1.SL.TZ1.T_2c:
Write down the range of the animal speeds.
-
19M.1.SL.TZ1.T_2d.i:
For these eight animals find the mean speed.
-
19M.1.SL.TZ1.T_2d.ii:
For these eight animals write down the standard deviation.
-
18M.2.SL.TZ1.T_2a:
State the alternative hypothesis.
-
18M.2.SL.TZ1.T_2b:
Calculate the expected frequency of flights travelling at most 500 km and arriving slightly delayed.
-
18M.2.SL.TZ1.T_2c:
Write down the number of degrees of freedom.
-
18M.2.SL.TZ1.T_2d.i:
Write down the χ2 statistic.
-
18M.2.SL.TZ1.T_2d.ii:
Write down the associated p-value.
-
18M.2.SL.TZ1.T_2e:
State, with a reason, whether you would reject the null hypothesis.
-
18M.2.SL.TZ1.T_2f:
Write down the probability that this flight arrived on time.
-
18M.2.SL.TZ1.T_2g:
Given that this flight was not heavily delayed, find the probability that it travelled between 500 km and 5000 km.
-
18M.2.SL.TZ1.T_2h:
Two flights are chosen at random from those which were slightly delayed.
Find the probability that each of these flights travelled at least 5000 km.
-
18M.1.SL.TZ2.T_7a:
State the number of boys who answered questions in Portuguese.
-
18M.1.SL.TZ2.T_7b:
Find the probability that the boy answered questions in Hindi.
-
18M.1.SL.TZ2.T_7c:
Two girls are selected at random.
Calculate the probability that one girl answered questions in Mandarin and the other answered questions in Hindi.
-
17M.1.SL.TZ2.T_7a:
Write down an equation, in terms of and , for the total number of times the die was rolled.
-
17M.1.SL.TZ2.T_7b:
Using the mean score, write down a second equation in terms of and .
-
17M.1.SL.TZ2.T_7c:
Find the value of and of .
-
18N.1.SL.TZ0.T_2a:
Write down the modal length of the rods.
-
18N.1.SL.TZ0.T_2b:
Find the median length of the rods.
-
18N.1.SL.TZ0.T_2c.i:
Calculate the lower quartile.
-
18N.1.SL.TZ0.T_2c.ii:
Calculate the interquartile range.
-
19M.1.SL.TZ1.T_5a:
Complete the cumulative frequency table.
-
19M.1.SL.TZ1.T_5b:
Write down the probability that a bouquet of roses sold is not small.
-
19M.1.SL.TZ1.T_5c:
A customer buys a large bouquet.
Find the probability that there are 12 roses in this bouquet.
-
18M.1.SL.TZ1.T_6a:
Write down the median.
-
18M.1.SL.TZ1.T_6b:
Complete the table.
-
18M.1.SL.TZ1.T_6c.i:
Write down the mid-interval value for the 100 < x ≤ 150 group.
-
18M.1.SL.TZ1.T_6c.ii:
Using the table, calculate an estimate for the mean number of people being followed on the social media website by these 160 students.
-
18M.1.SL.TZ2.T_12a:
Write down the mid-interval value for 10 ≤ t < 15.
-
18M.1.SL.TZ2.T_12b.i:
Write down the total number of customers in terms of k.
-
18M.1.SL.TZ2.T_12b.ii:
Calculate the value of k.
-
18M.1.SL.TZ2.T_12c:
Hence, complete the histogram.
-
17N.2.SL.TZ0.T_1a:
State whether is a discrete or a continuous variable.
-
17N.2.SL.TZ0.T_1b.i:
Write down, for , the modal class;
-
17N.2.SL.TZ0.T_1b.ii:
Write down, for , the mid-interval value of the modal class.
-
17N.2.SL.TZ0.T_1c.i:
Use your graphic display calculator to estimate the mean of ;
-
17N.2.SL.TZ0.T_1c.ii:
Use your graphic display calculator to estimate the standard deviation of .
-
17N.2.SL.TZ0.T_1d:
Find the expected frequency of students choosing the Science category and obtaining 31 to 40 correct answers.
-
17N.2.SL.TZ0.T_1e.i:
Write down the null hypothesis for this test;
-
17N.2.SL.TZ0.T_1e.ii:
Write down the number of degrees of freedom.
-
17N.2.SL.TZ0.T_1f.i:
Write down the -value for the test;
-
17N.2.SL.TZ0.T_1f.ii:
Write down the statistic.
-
17N.2.SL.TZ0.T_1g:
State the result of the test. Give a reason for your answer.
-
18N.2.SL.TZ0.T_3a.i:
Find the median of the examination results.
-
18N.2.SL.TZ0.T_3a.ii:
Find the interquartile range.
-
18N.2.SL.TZ0.T_3b:
Find the final examination result required to obtain the highest possible grade.
-
18N.2.SL.TZ0.T_3c.i:
Write down the modal class.
-
18N.2.SL.TZ0.T_3c.ii:
Write down the mid-interval value of the modal class.
-
18N.2.SL.TZ0.T_3d.i:
Calculate an estimate of the mean examination result.
-
18N.2.SL.TZ0.T_3d.ii:
Calculate an estimate of the standard deviation, giving your answer correct to three decimal places.
-
18N.2.SL.TZ0.T_3e:
The teacher sets a grade boundary that is one standard deviation below the mean.
Use the cumulative frequency graph to estimate the number of students whose final examination result was below this grade boundary.
-
19M.1.SL.TZ2.T_12a.i:
.
-
19M.1.SL.TZ2.T_12a.ii:
.
-
19M.1.SL.TZ2.T_12b:
On the same grid, complete the cumulative frequency curve for these data.
-
19M.1.SL.TZ2.T_12c:
Use the cumulative frequency curve to find an estimate for the number of students who worked at most 35 hours per month.
-
17N.1.SL.TZ0.T_1a.i:
For the students in this group find the mean age;
-
17N.1.SL.TZ0.T_1a.ii:
For the students in this group write down the median age.
-
17N.1.SL.TZ0.T_1b:
Draw a box-and-whisker diagram, for these students’ ages, on the following grid.

-
18M.2.SL.TZ2.T_2a:
Find the number of buses that travelled a distance between 15000 and 20000 kilometres.
-
18M.2.SL.TZ2.T_2b.i:
Use the cumulative frequency curve to find the median distance.
-
18M.2.SL.TZ2.T_2b.ii:
Use the cumulative frequency curve to find the lower quartile.
-
18M.2.SL.TZ2.T_2b.iii:
Use the cumulative frequency curve to find the upper quartile.
-
18M.2.SL.TZ2.T_2c:
Hence write down the interquartile range.
-
18M.2.SL.TZ2.T_2d:
Write down the percentage of buses that travelled a distance greater than the upper quartile.
-
18M.2.SL.TZ2.T_2e:
Find the number of buses that travelled a distance less than or equal to 12 000 km.
-
18M.2.SL.TZ2.T_2f:
Find the value of m.
-
18M.2.SL.TZ2.T_2g:
The smallest distance travelled by one of the buses was 2500 km.
The longest distance travelled by one of the buses was 23 000 km.On graph paper, draw a box-and-whisker diagram for these data. Use a scale of 2 cm to represent 5000 km.
-
19M.1.SL.TZ2.T_6a:
State what 13 represents in the given diagram.
-
19M.1.SL.TZ2.T_6b.i:
Write down the interquartile range for this data.
-
19M.1.SL.TZ2.T_6b.ii:
Write down the approximate number of snacks whose amount of sugar ranges from 18 to 20 grams.
-
19M.1.SL.TZ2.T_6c:
The health inspector visits two school cafeterias. She inspects the same number of meals at each cafeteria. The data is shown in the following box-and-whisker diagrams.
Meals prepared in the school cafeterias are required to have less than 10 grams of sugar.
State, giving a reason, which school cafeteria has more meals that do not meet the requirement.
-
16N.1.SL.TZ0.T_2a:
Giving your answer to one decimal place, write down the value of
(i) the median level of Vitamin C content of the oranges in the sample;
(ii) the lower quartile;
(iii) the upper quartile.
-
16N.1.SL.TZ0.T_2b:
Draw a box-and-whisker diagram on the grid below to represent the Vitamin C content, in milligrams, for this sample.

-
20N.1.SL.TZ0.S_8a:
Find the value of .
-
20N.1.SL.TZ0.S_8b:
Write down the value of the median distance in kilometres (km).
-
20N.1.SL.TZ0.S_8c:
Find the value of .
-
20N.1.SL.TZ0.S_8d:
Find .
-
20N.1.SL.TZ0.S_8e:
The first athletes that completed the race won a prize.
Given that an athlete took between and minutes to complete the race, calculate the probability that they won a prize.
-
20N.1.SL.TZ0.T_3a:
Write down the modal group for these data.
-
20N.1.SL.TZ0.T_3b:
Use your graphic display calculator to find an estimate of the standard deviation of the weights of mangoes from this harvest.
-
20N.1.SL.TZ0.T_3c:
On the grid below, draw a histogram for the data in the table.
-
21M.1.SL.TZ1.4a:
Find the minimum possible value of .
-
21M.1.SL.TZ1.4b:
Hence, find the minimum possible value of .
-
21M.1.SL.TZ2.7a:
Find the median number of hours per week these Year 12 students spend doing homework.
-
21M.1.SL.TZ2.7b:
Given that of these Year 12 students spend more than hours per week doing homework, find the value of .
-
21M.1.SL.TZ2.7c:
Find the value of and the value of .
-
21M.1.SL.TZ2.7d:
Estimate the number of Year 12 students that spend more than hours each week doing homework.
-
21M.1.SL.TZ2.7e.i:
Explain why this sampling method might not provide an accurate representation of the amount of time all of the students in the school spend doing homework.
-
21M.1.SL.TZ2.7e.ii:
Suggest a more appropriate sampling method.
-
22M.1.SL.TZ1.3a:
Find the largest value of that would not be considered an outlier.
-
22M.2.SL.TZ2.5a:
State the median reaction time after sleeping well.
-
22M.2.SL.TZ2.5c:
State why it appears that the mean reaction time is greater than the median reaction time.
-
22M.2.SL.TZ2.5d:
Now consider the two box and whisker diagrams.
Comment on whether these box and whisker diagrams provide any evidence that might suggest that not sleeping well causes an increase in reaction time.
SL 4.3—Mean, median, mode. Mean of grouped data, standard deviation. Quartiles, IQR
-
18M.1.AHL.TZ2.H_3a:
Find the value of p.
-
18M.1.AHL.TZ2.H_3b.i:
Find μ, the expected value of X.
-
18M.1.AHL.TZ2.H_3b.ii:
Find P(X > μ).
-
19M.2.AHL.TZ1.H_3a.i:
Find the mean.
-
19M.2.AHL.TZ1.H_3a.ii:
Find the standard deviation.
-
19M.2.AHL.TZ1.H_3b.i:
the mean.
-
19M.2.AHL.TZ1.H_3b.ii:
the standard deviation.
-
19M.2.AHL.TZ1.H_3c:
A ninth student also takes the test.
Explain why the median is unchanged.
-
17M.2.AHL.TZ2.H_1a:
One of the players is chosen at random. Find the probability that this player’s score was 5 or more.
-
17M.2.AHL.TZ2.H_1b:
Calculate the mean score.
-
16N.2.SL.TZ0.S_8a:
Find the mean number of hours spent browsing the Internet.
-
16N.2.SL.TZ0.S_8b:
During week 2, the students worked on a major project and they each spent an additional five hours browsing the Internet. For week 2, write down
(i) the mean;
(ii) the standard deviation.
-
16N.2.SL.TZ0.S_8c:
During week 3 each student spent 5% less time browsing the Internet than during week 1. For week 3, find
(i) the median;
(ii) the variance.
-
18M.1.SL.TZ1.S_2a:
Find the value of the interquartile range.
-
18M.1.SL.TZ1.S_2b:
One student sent k text messages, where k > 11 . Given that k is an outlier, find the least value of k.
-
17M.2.SL.TZ1.S_1a.i:
Write down the mode.
-
17M.2.SL.TZ1.S_1a.ii:
Find the value of the range.
-
17M.2.SL.TZ1.S_1b.i:
Find the mean.
-
17M.2.SL.TZ1.S_1b.ii:
Find the variance.
-
19M.2.SL.TZ1.S_1a:
For these data, find the mean distance from a student’s home to school.
-
19M.2.SL.TZ1.S_1b:
Find the value of .
-
19M.2.SL.TZ1.S_1c:
Find the interquartile range.
-
19M.1.SL.TZ2.S_8a:
The range of the data is 16. Find the value of .
-
19M.1.SL.TZ2.S_8b:
Find the value of the interquartile range.
-
19M.1.SL.TZ2.S_8c:
Find the mean number of hours that the girls in this group spent watching television that week.
-
19M.1.SL.TZ2.S_8d.i:
Find the total number of hours the group of boys spent watching television that week.
-
19M.1.SL.TZ2.S_8d.ii:
Find the mean number of hours that all 30 girls and boys spent watching television that week.
-
19M.1.SL.TZ2.S_8e.i:
the mean number of hours that the group of boys spent watching television.
-
18M.1.SL.TZ2.S_3a:
Find n.
-
18M.1.SL.TZ2.S_3b.i:
Write down the value of the new mean.
-
18M.1.SL.TZ2.S_3b.ii:
Find the value of the new variance.
-
17M.1.SL.TZ2.S_8a.i:
Find the median number of hours worked by the employees.
-
17M.1.SL.TZ2.S_8a.ii:
Write down the number of employees who worked 50 hours or less.
-
17M.1.SL.TZ2.S_8b.i:
Find the amount of money an employee earned for working 40 hours;
-
17M.1.SL.TZ2.S_8b.ii:
Find the amount of money an employee earned for working 43 hours.
-
17M.1.SL.TZ2.S_8c:
Find the number of employees who earned £200 or less.
-
17M.1.SL.TZ2.S_8d:
Only 10 employees earned more than £. Find the value of .
-
19M.1.SL.TZ1.T_2a:
State whether speed is a continuous or discrete variable.
-
19M.1.SL.TZ1.T_2b:
Write down the median speed for these animals.
-
19M.1.SL.TZ1.T_2c:
Write down the range of the animal speeds.
-
19M.1.SL.TZ1.T_2d.i:
For these eight animals find the mean speed.
-
19M.1.SL.TZ1.T_2d.ii:
For these eight animals write down the standard deviation.
-
18M.2.SL.TZ1.T_2a:
State the alternative hypothesis.
-
18M.2.SL.TZ1.T_2b:
Calculate the expected frequency of flights travelling at most 500 km and arriving slightly delayed.
-
18M.2.SL.TZ1.T_2c:
Write down the number of degrees of freedom.
-
18M.2.SL.TZ1.T_2d.i:
Write down the χ2 statistic.
-
18M.2.SL.TZ1.T_2d.ii:
Write down the associated p-value.
-
18M.2.SL.TZ1.T_2e:
State, with a reason, whether you would reject the null hypothesis.
-
18M.2.SL.TZ1.T_2f:
Write down the probability that this flight arrived on time.
-
18M.2.SL.TZ1.T_2g:
Given that this flight was not heavily delayed, find the probability that it travelled between 500 km and 5000 km.
-
18M.2.SL.TZ1.T_2h:
Two flights are chosen at random from those which were slightly delayed.
Find the probability that each of these flights travelled at least 5000 km.
-
17M.1.SL.TZ2.T_7a:
Write down an equation, in terms of and , for the total number of times the die was rolled.
-
17M.1.SL.TZ2.T_7b:
Using the mean score, write down a second equation in terms of and .
-
17M.1.SL.TZ2.T_7c:
Find the value of and of .
-
18N.1.SL.TZ0.T_2a:
Write down the modal length of the rods.
-
18N.1.SL.TZ0.T_2b:
Find the median length of the rods.
-
18N.1.SL.TZ0.T_2c.i:
Calculate the lower quartile.
-
18N.1.SL.TZ0.T_2c.ii:
Calculate the interquartile range.
-
18M.1.SL.TZ1.T_6a:
Write down the median.
-
18M.1.SL.TZ1.T_6b:
Complete the table.
-
18M.1.SL.TZ1.T_6c.i:
Write down the mid-interval value for the 100 < x ≤ 150 group.
-
18M.1.SL.TZ1.T_6c.ii:
Using the table, calculate an estimate for the mean number of people being followed on the social media website by these 160 students.
-
18M.1.SL.TZ2.T_12a:
Write down the mid-interval value for 10 ≤ t < 15.
-
18M.1.SL.TZ2.T_12b.i:
Write down the total number of customers in terms of k.
-
18M.1.SL.TZ2.T_12b.ii:
Calculate the value of k.
-
18M.1.SL.TZ2.T_12c:
Hence, complete the histogram.
-
17N.2.SL.TZ0.T_1a:
State whether is a discrete or a continuous variable.
-
17N.2.SL.TZ0.T_1b.i:
Write down, for , the modal class;
-
17N.2.SL.TZ0.T_1b.ii:
Write down, for , the mid-interval value of the modal class.
-
17N.2.SL.TZ0.T_1c.i:
Use your graphic display calculator to estimate the mean of ;
-
17N.2.SL.TZ0.T_1c.ii:
Use your graphic display calculator to estimate the standard deviation of .
-
17N.2.SL.TZ0.T_1d:
Find the expected frequency of students choosing the Science category and obtaining 31 to 40 correct answers.
-
17N.2.SL.TZ0.T_1e.i:
Write down the null hypothesis for this test;
-
17N.2.SL.TZ0.T_1e.ii:
Write down the number of degrees of freedom.
-
17N.2.SL.TZ0.T_1f.i:
Write down the -value for the test;
-
17N.2.SL.TZ0.T_1f.ii:
Write down the statistic.
-
17N.2.SL.TZ0.T_1g:
State the result of the test. Give a reason for your answer.
-
18N.2.SL.TZ0.T_3a.i:
Find the median of the examination results.
-
18N.2.SL.TZ0.T_3a.ii:
Find the interquartile range.
-
18N.2.SL.TZ0.T_3b:
Find the final examination result required to obtain the highest possible grade.
-
18N.2.SL.TZ0.T_3c.i:
Write down the modal class.
-
18N.2.SL.TZ0.T_3c.ii:
Write down the mid-interval value of the modal class.
-
18N.2.SL.TZ0.T_3d.i:
Calculate an estimate of the mean examination result.
-
18N.2.SL.TZ0.T_3d.ii:
Calculate an estimate of the standard deviation, giving your answer correct to three decimal places.
-
18N.2.SL.TZ0.T_3e:
The teacher sets a grade boundary that is one standard deviation below the mean.
Use the cumulative frequency graph to estimate the number of students whose final examination result was below this grade boundary.
-
17N.1.SL.TZ0.T_1a.i:
For the students in this group find the mean age;
-
17N.1.SL.TZ0.T_1a.ii:
For the students in this group write down the median age.
-
17N.1.SL.TZ0.T_1b:
Draw a box-and-whisker diagram, for these students’ ages, on the following grid.

-
18M.2.SL.TZ2.T_2a:
Find the number of buses that travelled a distance between 15000 and 20000 kilometres.
-
18M.2.SL.TZ2.T_2b.i:
Use the cumulative frequency curve to find the median distance.
-
18M.2.SL.TZ2.T_2b.ii:
Use the cumulative frequency curve to find the lower quartile.
-
18M.2.SL.TZ2.T_2b.iii:
Use the cumulative frequency curve to find the upper quartile.
-
18M.2.SL.TZ2.T_2c:
Hence write down the interquartile range.
-
18M.2.SL.TZ2.T_2d:
Write down the percentage of buses that travelled a distance greater than the upper quartile.
-
18M.2.SL.TZ2.T_2e:
Find the number of buses that travelled a distance less than or equal to 12 000 km.
-
18M.2.SL.TZ2.T_2f:
Find the value of m.
-
18M.2.SL.TZ2.T_2g:
The smallest distance travelled by one of the buses was 2500 km.
The longest distance travelled by one of the buses was 23 000 km.On graph paper, draw a box-and-whisker diagram for these data. Use a scale of 2 cm to represent 5000 km.
-
19M.1.SL.TZ2.T_6a:
State what 13 represents in the given diagram.
-
19M.1.SL.TZ2.T_6b.i:
Write down the interquartile range for this data.
-
19M.1.SL.TZ2.T_6b.ii:
Write down the approximate number of snacks whose amount of sugar ranges from 18 to 20 grams.
-
19M.1.SL.TZ2.T_6c:
The health inspector visits two school cafeterias. She inspects the same number of meals at each cafeteria. The data is shown in the following box-and-whisker diagrams.
Meals prepared in the school cafeterias are required to have less than 10 grams of sugar.
State, giving a reason, which school cafeteria has more meals that do not meet the requirement.
-
16N.1.SL.TZ0.T_2a:
Giving your answer to one decimal place, write down the value of
(i) the median level of Vitamin C content of the oranges in the sample;
(ii) the lower quartile;
(iii) the upper quartile.
-
16N.1.SL.TZ0.T_2b:
Draw a box-and-whisker diagram on the grid below to represent the Vitamin C content, in milligrams, for this sample.

-
18M.1.SL.TZ1.T_2a:
Find the value of x.
-
18M.1.SL.TZ1.T_2b.i:
Find the standard deviation
-
18M.1.SL.TZ1.T_2b.ii:
Find the interquartile range.
-
16N.2.SL.TZ0.T_1a:
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the -axis and 2 cm to represent 10 points on the -axis.
-
16N.2.SL.TZ0.T_1b:
(i) , the mean number of hours spent on social media;
(ii) , the mean number of IB Diploma points.
-
16N.2.SL.TZ0.T_1c:
Plot the point on your scatter diagram and label this point M.
-
16N.2.SL.TZ0.T_1d:
Write down the value of , the Pearson’s product–moment correlation coefficient, for these data.
-
16N.2.SL.TZ0.T_1e:
Write down the equation of the regression line on for these eight male students.
-
16N.2.SL.TZ0.T_1f:
Draw the regression line, from part (e), on your scatter diagram.
-
16N.2.SL.TZ0.T_1g:
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.
-
16N.2.SL.TZ0.T_1h:
Write down a reason why this estimate is not reliable.
-
17M.2.SL.TZ1.T_5a.i:
Calculate the mean test grade of the students;
-
17M.2.SL.TZ1.T_5a.ii:
Calculate the standard deviation.
-
17M.2.SL.TZ1.T_5b:
Find the median test grade of the students.
-
17M.2.SL.TZ1.T_5c:
Find the interquartile range.
-
17M.2.SL.TZ1.T_5d:
Find the probability that this student scored a grade 5 or higher.
-
17M.2.SL.TZ1.T_5e:
Given that the first student chosen at random scored a grade 5 or higher, find the probability that both students scored a grade 6.
-
17M.2.SL.TZ1.T_5f.i:
Calculate the probability that a student chosen at random spent at least 90 minutes preparing for the test.
-
17M.2.SL.TZ1.T_5f.ii:
Calculate the expected number of students that spent at least 90 minutes preparing for the test.
-
19M.2.SL.TZ1.T_3a:
Write down the total number of people, from this group, who are pet owners.
-
19M.2.SL.TZ1.T_3b:
Write down the modal number of pets.
-
19M.2.SL.TZ1.T_3c.i:
For these data, write down the median number of pets.
-
19M.2.SL.TZ1.T_3c.ii:
For these data, write down the lower quartile.
-
19M.2.SL.TZ1.T_3c.iii:
For these data, write down the upper quartile.
-
19M.2.SL.TZ1.T_3d:
Write down the ratio of teenagers to non-teenagers in its simplest form.
-
19M.2.SL.TZ1.T_3e.i:
State the null hypothesis.
-
19M.2.SL.TZ1.T_3e.ii:
State the alternative hypothesis.
-
19M.2.SL.TZ1.T_3f:
Write down the number of degrees of freedom for this test.
-
19M.2.SL.TZ1.T_3g:
Calculate the expected number of teenagers that prefer cats.
-
19M.2.SL.TZ1.T_3h:
Use your graphic display calculator to find the -value for this test.
-
19M.2.SL.TZ1.T_3i:
State the conclusion for this test. Give a reason for your answer.
-
19M.1.SL.TZ2.T_14a.ii:
Find the price that is two standard deviations above the mean price.
-
19M.1.SL.TZ2.T_14b:
Find the probability that the price of a kilogram of tomatoes, chosen at random, will be between 2.00 and 3.00 euro.
-
19M.1.SL.TZ2.T_14c:
To stimulate reasonable pricing, the city offers a free permit to the sellers whose price of a kilogram of tomatoes is in the lowest 20 %.
Find the highest price that a seller can charge and still receive a free permit.
-
20N.1.SL.TZ0.S_8a:
Find the value of .
-
20N.1.SL.TZ0.S_8b:
Write down the value of the median distance in kilometres (km).
-
20N.1.SL.TZ0.S_8c:
Find the value of .
-
20N.1.SL.TZ0.S_8d:
Find .
-
20N.1.SL.TZ0.S_8e:
The first athletes that completed the race won a prize.
Given that an athlete took between and minutes to complete the race, calculate the probability that they won a prize.
-
20N.2.SL.TZ0.S_9a:
Find the probability that it will take Fiona between minutes and minutes to walk to the bus stop.
-
20N.2.SL.TZ0.S_9b:
Find .
-
20N.2.SL.TZ0.S_9c:
Find the probability that the bus journey takes less than minutes.
-
20N.2.SL.TZ0.S_9d:
Find the probability that Fiona will arrive on time.
-
20N.2.SL.TZ0.S_9e:
This year, Fiona will go to school on days.
Calculate the number of days Fiona is expected to arrive on time.
-
20N.1.SL.TZ0.T_3a:
Write down the modal group for these data.
-
20N.1.SL.TZ0.T_3b:
Use your graphic display calculator to find an estimate of the standard deviation of the weights of mangoes from this harvest.
-
20N.1.SL.TZ0.T_3c:
On the grid below, draw a histogram for the data in the table.
-
20N.1.SL.TZ0.T_7a:
Find the height of Flower null.
-
20N.1.SL.TZ0.T_7b:
Using this information, write down an equation in and .
-
20N.1.SL.TZ0.T_7c:
Write down a second equation in and .
-
20N.1.SL.TZ0.T_7d.i:
Using your answers to parts (b) and (c), find the height of Flower .
-
20N.1.SL.TZ0.T_7d.ii:
Using your answers to parts (b) and (c), find the height of Flower .
-
EXN.2.SL.TZ0.1:
A data set consisting of test scores has mean . One test score of requires a second marking and is removed from the data set.
Find the mean of the remaining test scores.
-
22M.1.SL.TZ1.3b.i:
One of the adults surveyed is years old. Estimate the age of their eldest child.
-
22M.1.SL.TZ1.3b.ii:
Find the mean age of all the adults surveyed.
-
22M.2.SL.TZ1.2a:
Find the value of .
-
22M.2.SL.TZ1.2b:
Find the standard deviation.
SL 4.4—Pearsons, scatter diagrams, eqn of y on x
-
SPM.2.SL.TZ0.5a:
Find the value of a and the value of b.
-
SPM.2.SL.TZ0.5b:
Let L2 be the regression line of y on x. The lines L1 and L2 pass through the same point with coordinates (p , q).
Find the value of p and the value of q.
-
SPM.2.AHL.TZ0.4a:
Find the value of a and the value of b.
-
SPM.2.AHL.TZ0.4b:
Find the value of p and the value of q.
-
SPM.2.AHL.TZ0.4c:
Jennifer was absent for the first test but scored 29 marks on the second test. Use an appropriate regression equation to estimate Jennifer’s mark on the first test.
-
17M.2.SL.TZ1.T_1a:
Find the range of the average body weights for these seven species of mammal.
-
17M.2.SL.TZ1.T_1b.i:
For the data from these seven species calculate , the Pearson’s product–moment correlation coefficient;
-
17M.2.SL.TZ1.T_1b.ii:
For the data from these seven species describe the correlation between the average body weight and the average weight of the brain.
-
17M.2.SL.TZ1.T_1c:
Write down the equation of the regression line on , in the form .
-
17M.2.SL.TZ1.T_1d:
Use your regression line to estimate the average weight of the brain of grey wolves.
-
17M.2.SL.TZ1.T_1e:
Find the percentage error in your estimate in part (d).
-
17M.2.SL.TZ1.T_1f:
State whether it is valid to use the regression line to estimate the average weight of the brain of mice. Give a reason for your answer.
-
18N.2.SL.TZ0.T_1a.i:
Use your graphic display calculator to write down , the mean project mark.
-
18N.2.SL.TZ0.T_1a.ii:
Use your graphic display calculator to write down , the mean examination score.
-
18N.2.SL.TZ0.T_1a.iii:
Use your graphic display calculator to write down r , Pearson’s product–moment correlation coefficient.
-
18N.2.SL.TZ0.T_1b.i:
Find the exact value of m and of c for these data.
-
18N.2.SL.TZ0.T_1b.ii:
Show that the point M (, ) lies on the regression line y on x.
-
18N.2.SL.TZ0.T_1c.i:
Use the regression line y on x to estimate Jerome’s examination score.
-
18N.2.SL.TZ0.T_1c.ii:
Justify whether it is valid to use the regression line y on x to estimate Jerome’s examination score.
-
18N.2.SL.TZ0.T_1d:
In his final IB examination Jerome scored 65.
Calculate the percentage error in Jerome’s estimated examination score.
-
18M.3.AHL.TZ0.Hsp_4a:
State suitable hypotheses to investigate whether or not a negative linear association exists between X and Y.
-
18M.3.AHL.TZ0.Hsp_4b.i:
Determine the p-value.
-
18M.3.AHL.TZ0.Hsp_4b.ii:
State your conclusion at the 1 % significance level.
-
18M.3.AHL.TZ0.Hsp_4c.i:
Show that Cov(U, V) = E(UV) − E(U)E(V).
-
18M.3.AHL.TZ0.Hsp_4c.ii:
Hence show that if U, V are independent random variables then the population product moment correlation coefficient, ρ, is zero.
-
18M.2.SL.TZ1.S_8a:
Find the value of a and of b.
-
18M.2.SL.TZ1.S_8b:
Use the regression equation to estimate the value of y when x = 3.57.
-
18M.2.SL.TZ1.S_8c:
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
-
17N.2.SL.TZ0.S_8a:
Write down the value of and of .
-
17N.2.SL.TZ0.S_8b:
Use this regression line to estimate the monthly honey production from a hive that has 270 bees.
-
17N.2.SL.TZ0.S_8c:
Write down the number of low production hives.
-
17N.2.SL.TZ0.S_8d.i:
Find the value of ;
-
17N.2.SL.TZ0.S_8d.ii:
Find the number of hives that have a high production.
-
17N.2.SL.TZ0.S_8e:
Adam decides to increase the number of bees in each low production hive. Research suggests that there is a probability of 0.75 that a low production hive becomes a regular production hive. Calculate the probability that 30 low production hives become regular production hives.
-
18M.2.SL.TZ2.S_1a.i:
Find the value of a and of b.
-
18M.2.SL.TZ2.S_1a.ii:
Write down the correlation coefficient.
-
18M.2.SL.TZ2.S_1b:
Use your equation to estimate the mean weight of a child that is 1.95 years old.
-
17M.2.SL.TZ2.S_2a.i:
Find the value of and of .
-
17M.2.SL.TZ2.S_2a.ii:
Write down the value of .
-
17M.2.SL.TZ2.S_2b:
Use the regression equation to estimate the number of visitors on a day when the maximum temperature is 15 °C.
-
17M.1.SL.TZ1.S_4a.i:
Write down the independent variable.
-
17M.1.SL.TZ1.S_4a.ii:
Write down the boiling temperature of the liquid.
-
17M.1.SL.TZ1.S_4b:
Jim describes the correlation as very strong. Circle the value below which best represents the correlation coefficient.
-
17M.1.SL.TZ1.S_4c:
Jim’s model is , for . Use his model to predict the decrease in temperature for any 2 minute interval.
-
18N.2.SL.TZ0.S_2a.i:
Find the value of a and of b.
-
18N.2.SL.TZ0.S_2a.ii:
Write down the correlation coefficient.
-
18N.2.SL.TZ0.S_2b:
Another athlete on this sports team has a hand length of 21.5 cm. Use the regression equation to estimate the height of this athlete.
-
19M.2.SL.TZ1.S_5a:
Write down the value of and of .
-
19M.2.SL.TZ1.S_5b:
Use the model to predict how many edge pieces she had found when she had sorted a total of 750 pieces.
-
19M.2.SL.TZ2.S_1a.i:
Write down the value of and of .
-
19M.2.SL.TZ2.S_1a.ii:
Find the correlation coefficient.
-
19M.2.SL.TZ2.S_1b:
Use the regression equation to estimate the BMI of an adult man whose waist size is 95 cm.
-
16N.2.SL.TZ0.T_1a:
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the -axis and 2 cm to represent 10 points on the -axis.
-
16N.2.SL.TZ0.T_1b:
(i) , the mean number of hours spent on social media;
(ii) , the mean number of IB Diploma points.
-
16N.2.SL.TZ0.T_1c:
Plot the point on your scatter diagram and label this point M.
-
16N.2.SL.TZ0.T_1d:
Write down the value of , the Pearson’s product–moment correlation coefficient, for these data.
-
16N.2.SL.TZ0.T_1e:
Write down the equation of the regression line on for these eight male students.
-
16N.2.SL.TZ0.T_1f:
Draw the regression line, from part (e), on your scatter diagram.
-
16N.2.SL.TZ0.T_1g:
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.
-
16N.2.SL.TZ0.T_1h:
Write down a reason why this estimate is not reliable.
-
18M.1.SL.TZ1.T_4a.i:
For these data, find Pearson’s product-moment correlation coefficient, r.
-
18M.1.SL.TZ1.T_4a.ii:
For these data, find the equation of the regression line y on x.
-
18M.1.SL.TZ1.T_4b:
Using the equation of the regression line, estimate the concentration of dissolved oxygen in the river when the temperature is 18 °C.
-
17N.1.SL.TZ0.T_5a:
Find the mean number of hours that the people surveyed watch television per week.
-
17N.1.SL.TZ0.T_5b:
Draw the regression line on the scatter diagram.
-
17N.1.SL.TZ0.T_5c:
By placing a tick (✔) in the correct box, determine which of the following statements is true:

-
17N.1.SL.TZ0.T_5d:
Diogo is 18 years old. Give a reason why the regression line should not be used to estimate the number of hours Diogo watches television per week.
-
17M.2.SL.TZ2.T_3a:
Draw a scatter diagram for this data. Use a scale of 2 cm for 5000 folders on the horizontal axis and 2 cm for 10 000 Euros on the vertical axis.
-
17M.2.SL.TZ2.T_3b.i:
Write down, for this set of data the mean number of folders produced, ;
-
17M.2.SL.TZ2.T_3b.ii:
Write down, for this set of data the mean production cost, .
-
17M.2.SL.TZ2.T_3c:
Label the point on the scatter diagram.
-
17M.2.SL.TZ2.T_3d:
Use your graphic display calculator to find the Pearson’s product–moment correlation coefficient, .
-
17M.2.SL.TZ2.T_3e:
State a reason why the regression line on is appropriate to model the relationship between these variables.
-
17M.2.SL.TZ2.T_3f:
Use your graphic display calculator to find the equation of the regression line on .
-
17M.2.SL.TZ2.T_3g:
Draw the regression line on on the scatter diagram.
-
17M.2.SL.TZ2.T_3h:
Use the equation of the regression line to estimate the least number of folders that the factory needs to sell in a month to exceed its production cost for that month.
-
18M.1.SL.TZ2.T_1a:
Plot and label the point M on the scatter diagram.
-
18M.1.SL.TZ2.T_1b:
Draw the line of best fit, by eye, on the scatter diagram.
-
18M.1.SL.TZ2.T_1c:
Using your line of best fit, estimate the physics test score for a student with a score of 20 in their mathematics test.
-
19M.2.SL.TZ1.T_1a:
Draw a scatter diagram for temperature difference from 37 °C () against heartbeat (). Use a scale of 2 cm for 0.1 °C on the horizontal axis, starting with −0.3 °C. Use a scale of 1 cm for 2 heartbeats per minute on the vertical axis, starting with 60 beats per minute.
-
19M.2.SL.TZ1.T_1b.i:
Write down, for this set of data the mean temperature difference from 37 °C, .
-
19M.2.SL.TZ1.T_1b.ii:
Write down, for this set of data the mean number of heartbeats per minute, .
-
19M.2.SL.TZ1.T_1c:
Plot and label the point M(, ) on the scatter diagram.
-
19M.2.SL.TZ1.T_1d.i:
Use your graphic display calculator to find the Pearson’s product–moment correlation coefficient, .
-
19M.2.SL.TZ1.T_1d.ii:
Hence describe the correlation between temperature difference from 37 °C and heartbeat.
-
19M.2.SL.TZ1.T_1e:
Use your graphic display calculator to find the equation of the regression line on .
-
19M.2.SL.TZ1.T_1f:
Draw the regression line on on the scatter diagram.
-
19M.1.SL.TZ2.T_2a:
Find the equation of the regression line of on .
-
19M.1.SL.TZ2.T_2b:
Draw the regression line of on on the scatter diagram.
-
19M.1.SL.TZ2.T_2c:
In order to estimate the amount of oxygen consumed, this regression line is considered to be reliable for a temperature such that ≤ ≤ .
Write down the value of and of .
-
19N.3.AHL.TZ0.Hsp_1a.i:
State suitable hypotheses and to test Peter’s claim, using a two-tailed test.
-
19N.3.AHL.TZ0.Hsp_1a.ii:
Carry out a suitable test at the 5 % significance level. With reference to the -value, state your conclusion in the context of Peter’s claim.
-
19N.3.AHL.TZ0.Hsp_1b:
Peter uses the regression line of on as and calculates that a student with a Mathematics test score of 73 will have a running time of 101 seconds. Comment on the validity of his calculation.
-
19N.2.SL.TZ0.S_1a:
Write down the value of and of .
-
19N.2.SL.TZ0.S_1b:
Use your regression equation to predict the number of messages sent by a teenager that spent minutes talking on their phone in October.
-
20N.2.SL.TZ0.S_2a.i:
Find the value of and of .
-
20N.2.SL.TZ0.S_2a.ii:
Write down the correlation coefficient.
-
20N.2.SL.TZ0.S_2b:
Using the regression equation, estimate the number of hot chocolates that Lucy will sell on a day when the maximum temperature is .
-
EXN.2.SL.TZ0.4a.i:
Determine the value of Pearson’s product‐moment correlation coefficient, , for these data.
-
EXN.2.SL.TZ0.4a.ii:
Interpret, in context, the value of found in part (a) (i).
-
EXN.2.SL.TZ0.4b:
Find the equation of the regression line of on .
-
EXN.2.SL.TZ0.4c:
Use the regression equation from part (b) to predict this patient’s systolic blood pressure.
-
EXN.2.SL.TZ0.4d:
A ‐year‐old male patient enters the medical clinic for his appointment.
Explain why the regression equation from part (b) should not be used to predict this patient’s systolic blood pressure.
-
21M.2.SL.TZ1.2a:
Write down the value of and the value of .
-
21M.2.SL.TZ1.2b:
Use this model to predict the value of when .
-
21M.2.SL.TZ1.2c:
Write down the value of and the value of .
-
21M.2.SL.TZ1.2d:
Draw the line of best fit on the scatter diagram.
-
21M.2.SL.TZ2.1a.i:
Find the value of and the value of .
-
21M.2.SL.TZ2.1a.ii:
Write down the value of Pearson’s product-moment correlation coefficient, .
-
21M.2.SL.TZ2.1b:
Interpret, in context, the value of found in part (a)(i).
-
21M.2.SL.TZ2.1c:
On another day, Sarah visits the café to order a coffee. Seven customers have already ordered their coffee and are waiting to receive it.
Use the result from part (a)(i) to estimate Sarah’s waiting time to receive her coffee.
-
21N.2.SL.TZ0.1a:
Find Pearson’s product-moment correlation coefficient, , for these data.
-
21N.2.SL.TZ0.1b:
The relationship between the variables can be modelled by the regression equation . Write down the value of and the value of .
-
21N.2.SL.TZ0.1c:
One of these eight students was disappointed with her result and wished she had practised more. Based on the given data, determine how her score could have been expected to alter had she practised an extra five hours per week.
-
21N.2.AHL.TZ0.1a:
Find Pearson’s product-moment correlation coefficient, , for these data.
-
21N.2.AHL.TZ0.1b:
The relationship between the variables can be modelled by the regression equation . Write down the value of and the value of .
-
21N.2.AHL.TZ0.1c:
One of these eight students was disappointed with her result and wished she had practised more. Based on the given data, determine how her score could have been expected to alter had she practised an extra five hours per week.
-
21N.2.AHL.TZ0.1d:
Lucy asserts that the number of hours a student practises has a direct effect on their final diploma result. Comment on the validity of Lucy’s assertion.
-
21N.2.AHL.TZ0.1e:
Lucy suspected that each student had not been practising as much as they reported. In order to compensate for this, Lucy deducted a fixed number of hours per week from each of the students’ recorded hours.
State how, if at all, the value of would be affected.
-
22M.1.SL.TZ1.3b.i:
One of the adults surveyed is years old. Estimate the age of their eldest child.
-
22M.1.SL.TZ1.3b.ii:
Find the mean age of all the adults surveyed.
SL 4.5—Probability concepts, expected numbers
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
19M.2.SL.TZ1.S_10a.i:
Find the probability of rolling exactly one red face.
-
19M.2.SL.TZ1.S_10a.ii:
Find the probability of rolling two or more red faces.
-
19M.2.SL.TZ1.S_10b:
Show that, after a turn, the probability that Ted adds exactly $10 to his winnings is .
-
19M.2.SL.TZ1.S_10c.i:
Write down the value of .
-
19M.2.SL.TZ1.S_10c.ii:
Hence, find the value of .
-
19M.2.SL.TZ1.S_10d:
Ted will always have another turn if he expects an increase to his winnings.
Find the least value of for which Ted should end the game instead of having another turn.
-
17M.1.SL.TZ1.S_1a.i:
Find the value of ;
-
17M.1.SL.TZ1.S_1a.ii:
Find the value of .
-
17M.1.SL.TZ1.S_1b:
A girl is selected at random. Find the probability that she takes economics but not history.
-
18N.1.SL.TZ0.S_9a.i:
Find the probability, in terms of , that the game will end on her first draw.
-
18N.1.SL.TZ0.S_9a.ii:
Find the probability, in terms of , that the game will end on her second draw.
-
18N.1.SL.TZ0.S_9b.i:
third draw.
-
18N.1.SL.TZ0.S_9b.ii:
fourth draw.
-
18N.1.SL.TZ0.S_9c:
Hayley plays the game when = 5. She pays $20 to play and can earn money back depending on the number of draws it takes to obtain a blue marble. She earns no money back if she obtains a blue marble on her first draw. Let M be the amount of money that she earns back playing the game. This information is shown in the following table.
Find the value of so that this is a fair game.
-
18N.2.SL.TZ0.S_1a:
Write down the number of students in the group who take art class.
-
18N.2.SL.TZ0.S_1b.i:
the student does not take art class.
-
18N.2.SL.TZ0.S_1b.ii:
the student takes either art class or music class, but not both.
-
17N.1.SL.TZ0.T_7a:
Complete the Venn diagram for these students.

-
17N.1.SL.TZ0.T_7b:
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.
-
17N.1.SL.TZ0.T_7c:
Determine whether the events and are independent.
-
16N.2.SL.TZ0.T_2a:
Draw a Venn diagram to represent the given information, using sets labelled , and .
-
16N.2.SL.TZ0.T_2b:
Show that .
-
16N.2.SL.TZ0.T_2c:
Write down the value of .
-
16N.2.SL.TZ0.T_2d:
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.
-
18N.2.SL.TZ0.T_2a.i:
Find the number of students in the school that are taught in Spanish.
-
18N.2.SL.TZ0.T_2a.ii:
Find the number of students in the school that study Mathematics in English.
-
18N.2.SL.TZ0.T_2a.iii:
Find the number of students in the school that study both Biology and Mathematics.
-
18N.2.SL.TZ0.T_2b.i:
Write down .
-
18N.2.SL.TZ0.T_2b.ii:
Write down .
-
18N.2.SL.TZ0.T_2c.i:
Find the probability that this student studies Mathematics.
-
18N.2.SL.TZ0.T_2c.ii:
Find the probability that this student studies neither Biology nor Mathematics.
-
18N.2.SL.TZ0.T_2c.iii:
Find the probability that this student is taught in Spanish, given that the student studies Biology.
-
19M.1.SL.TZ2.T_5a:
Using the given information, complete the following Venn diagram.
-
19M.1.SL.TZ2.T_5b:
Find the number of surveyed students who did not like any of the three flavours.
-
19M.1.SL.TZ2.T_5c:
A student is chosen at random from the surveyed students.
Find the probability that this student likes kiwi fruit smoothies given that they like mango smoothies.
-
20N.1.SL.TZ0.S_8a:
Find the value of .
-
20N.1.SL.TZ0.S_8b:
Write down the value of the median distance in kilometres (km).
-
20N.1.SL.TZ0.S_8c:
Find the value of .
-
20N.1.SL.TZ0.S_8d:
Find .
-
20N.1.SL.TZ0.S_8e:
The first athletes that completed the race won a prize.
Given that an athlete took between and minutes to complete the race, calculate the probability that they won a prize.
-
20N.2.SL.TZ0.S_9a:
Find the probability that it will take Fiona between minutes and minutes to walk to the bus stop.
-
20N.2.SL.TZ0.S_9b:
Find .
-
20N.2.SL.TZ0.S_9c:
Find the probability that the bus journey takes less than minutes.
-
20N.2.SL.TZ0.S_9d:
Find the probability that Fiona will arrive on time.
-
20N.2.SL.TZ0.S_9e:
This year, Fiona will go to school on days.
Calculate the number of days Fiona is expected to arrive on time.
-
20N.1.SL.TZ0.T_6a.i:
Find the probability that the first ball chosen is labelled .
-
20N.1.SL.TZ0.T_6a.ii:
Find the probability that the first ball chosen is labelled or labelled .
-
20N.1.SL.TZ0.T_6b:
Find the probability that the second ball chosen is labelled , given that the first ball chosen was labelled .
-
20N.1.SL.TZ0.T_6c:
Find the probability that both balls chosen are labelled .
-
22M.1.SL.TZ2.9c:
Assuming that rolls of the die are independent, find the probability that Nicky wins the game.
SL 4.6—Combined, mutually exclusive, conditional, independence, prob diagrams
-
SPM.1.SL.TZ0.2:
Let A and B be events such that , and .
Find .
-
SPM.2.SL.TZ0.8a:
Find P(24.15 < X < 25).
-
SPM.2.SL.TZ0.8b.i:
Find , the standard deviation of X.
-
SPM.2.SL.TZ0.8b.ii:
Hence, find the probability that a seashell selected at random has a length greater than 26 mm.
-
SPM.2.SL.TZ0.8c:
Find E(Y).
-
SPM.2.SL.TZ0.8d:
Find the probability that exactly three of these seashells have a length greater than 26 mm.
-
SPM.2.SL.TZ0.8e:
A seashell selected at random has a length less than 26 mm.
Find the probability that its length is between 24.15 mm and 25 mm.
-
19M.1.SL.TZ1.T_7a:
Place the numbers and in the correct position on the Venn diagram.
-
19M.1.SL.TZ1.T_7b:
In the table indicate which two of the given statements are true by placing a tick (✔) in the right hand column.
-
19M.1.SL.TZ2.T_11a:
Write down the elements that belong to .
-
19M.1.SL.TZ2.T_11b.i:
Write down the elements that belong to .
-
19M.1.SL.TZ2.T_11b.ii:
Write down .
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
19M.2.AHL.TZ2.H_3a:
Complete the given probability tree diagram for Iqbal’s three attempts, labelling each branch with the correct probability.
-
19M.2.AHL.TZ2.H_3b:
Calculate the probability that Iqbal passes at least two of the papers he attempts.
-
19M.2.AHL.TZ2.H_3c:
Find the probability that Iqbal passes his third paper, given that he passed only one previous paper.
-
17N.2.AHL.TZ0.H_2a:
Find .
-
17N.2.AHL.TZ0.H_2b:
Find .
-
17N.2.AHL.TZ0.H_2c:
Hence show that events and are independent.
-
17M.2.AHL.TZ1.H_1a:
Calculate ;
-
17M.2.AHL.TZ1.H_1b:
Find .
-
18M.2.AHL.TZ1.H_8:
Each of the 25 students in a class are asked how many pets they own. Two students own three pets and no students own more than three pets. The mean and standard deviation of the number of pets owned by students in the class are and respectively.
Find the number of students in the class who do not own a pet.
-
18N.1.AHL.TZ0.H_1a:
By drawing a Venn diagram, or otherwise, find .
-
18N.1.AHL.TZ0.H_1b:
Show that the events and are not independent.
-
16N.1.AHL.TZ0.H_10a:
Show that .
-
16N.1.AHL.TZ0.H_10b:
(i) show that ;
(ii) hence find .
-
19M.2.AHL.TZ1.H_9a.i:
both a sandwich and a cake.
-
19M.2.AHL.TZ1.H_9a.ii:
only a sandwich.
-
19M.2.AHL.TZ1.H_9b.i:
Find the expected number of cakes sold on a typical day.
-
19M.2.AHL.TZ1.H_9b.ii:
Find the probability that more than 100 cakes will be sold on a typical day.
-
19M.2.AHL.TZ1.H_9c.i:
A customer is selected at random. Find the probability that the customer is male and buys a sandwich.
-
19M.2.AHL.TZ1.H_9c.ii:
A female customer is selected at random. Find the probability that she buys a sandwich.
-
18M.2.AHL.TZ1.H_6:
The mean number of squirrels in a certain area is known to be 3.2 squirrels per hectare of woodland. Within this area, there is a 56 hectare woodland nature reserve. It is known that there are currently at least 168 squirrels in this reserve.
Assuming the population of squirrels follow a Poisson distribution, calculate the probability that there are more than 190 squirrels in the reserve.
-
17M.1.AHL.TZ1.H_10a:
Find the value of .
-
17M.1.AHL.TZ1.H_10b.i:
By considering the graph of f write down the mean of ;
-
17M.1.AHL.TZ1.H_10b.ii:
By considering the graph of f write down the median of ;
-
17M.1.AHL.TZ1.H_10b.iii:
By considering the graph of f write down the mode of .
-
17M.1.AHL.TZ1.H_10c.i:
Show that .
-
17M.1.AHL.TZ1.H_10c.ii:
Hence state the interquartile range of .
-
17M.1.AHL.TZ1.H_10d:
Calculate .
-
17N.1.SL.TZ0.S_1a:
Complete the following tree diagram.

-
17N.1.SL.TZ0.S_1b:
Find the probability that exactly one of the selected balls is green.
-
18M.2.SL.TZ1.S_5a:
Find P(A ∩ B′ ).
-
18M.2.SL.TZ1.S_5b:
Given that P((A ∪ B)′ ) = 0.19, find P(A | B′ ).
-
18M.1.SL.TZ2.S_8a:
Copy and complete the following tree diagram.
-
18M.1.SL.TZ2.S_8b:
Find the probability that Pablo leaves home before 07:00 and is late for work.
-
18M.1.SL.TZ2.S_8c:
Find the probability that Pablo is late for work.
-
18M.1.SL.TZ2.S_8d:
Given that Pablo is late for work, find the probability that he left home before 07:00.
-
18M.1.SL.TZ2.S_8e:
Two days next week Pablo will drive to work. Find the probability that he will be late at least once.
-
19M.2.SL.TZ1.S_10a.i:
Find the probability of rolling exactly one red face.
-
19M.2.SL.TZ1.S_10a.ii:
Find the probability of rolling two or more red faces.
-
19M.2.SL.TZ1.S_10b:
Show that, after a turn, the probability that Ted adds exactly $10 to his winnings is .
-
19M.2.SL.TZ1.S_10c.i:
Write down the value of .
-
19M.2.SL.TZ1.S_10c.ii:
Hence, find the value of .
-
19M.2.SL.TZ1.S_10d:
Ted will always have another turn if he expects an increase to his winnings.
Find the least value of for which Ted should end the game instead of having another turn.
-
17M.1.SL.TZ1.S_1a.i:
Find the value of ;
-
17M.1.SL.TZ1.S_1a.ii:
Find the value of .
-
17M.1.SL.TZ1.S_1b:
A girl is selected at random. Find the probability that she takes economics but not history.
-
18N.1.SL.TZ0.S_9a.i:
Find the probability, in terms of , that the game will end on her first draw.
-
18N.1.SL.TZ0.S_9a.ii:
Find the probability, in terms of , that the game will end on her second draw.
-
18N.1.SL.TZ0.S_9b.i:
third draw.
-
18N.1.SL.TZ0.S_9b.ii:
fourth draw.
-
18N.1.SL.TZ0.S_9c:
Hayley plays the game when = 5. She pays $20 to play and can earn money back depending on the number of draws it takes to obtain a blue marble. She earns no money back if she obtains a blue marble on her first draw. Let M be the amount of money that she earns back playing the game. This information is shown in the following table.
Find the value of so that this is a fair game.
-
18N.2.SL.TZ0.S_1a:
Write down the number of students in the group who take art class.
-
18N.2.SL.TZ0.S_1b.i:
the student does not take art class.
-
18N.2.SL.TZ0.S_1b.ii:
the student takes either art class or music class, but not both.
-
19M.1.SL.TZ1.S_1a:
Find the value of .
-
19M.1.SL.TZ1.S_1b:
Find the value of .
-
19M.1.SL.TZ1.S_1c:
Find .
-
16N.1.SL.TZ0.S_5a:
Find .
-
16N.1.SL.TZ0.S_5b:
Find .
-
17N.2.SL.TZ0.S_4a:
Find the value of .
-
17N.2.SL.TZ0.S_4b:
Write down .
-
17N.2.SL.TZ0.S_4c:
Find .
-
18M.2.SL.TZ1.S_9a:
Find the probability that an orange weighs between 289 g and 310 g.
-
18M.2.SL.TZ1.S_9b.i:
Find the standardized value for 289 g.
-
18M.2.SL.TZ1.S_9b.ii:
Hence, find the value of σ.
-
18M.2.SL.TZ1.S_9c:
To the nearest gram, find the minimum weight of an orange that the grocer will buy.
-
18M.2.SL.TZ1.S_9d:
Find the probability that the grocer buys more than half the oranges in a box selected at random.
-
18M.2.SL.TZ1.S_9e:
The grocer selects two boxes at random.
Find the probability that the grocer buys more than half the oranges in each box.
-
17M.2.SL.TZ1.S_9a:
Find .
-
17M.2.SL.TZ1.S_9b:
Find the value of .
-
17M.2.SL.TZ1.S_9c:
Find .
-
17M.2.SL.TZ1.S_9d:
Given that , find .
-
19M.1.SL.TZ1.S_9a:
Find P(−1.6 < < 2.4). Write your answer in terms of and .
-
19M.1.SL.TZ1.S_9b:
Given that > −1.6, find the probability that z < 2.4 . Write your answer in terms of and .
-
19M.1.SL.TZ1.S_9c:
Write down the standardized value for .
-
19M.1.SL.TZ1.S_9d:
It is also known that P( > 2) = .
Find .
-
19M.2.SL.TZ2.S_9a:
Show that event A and event D are not independent.
-
19M.2.SL.TZ2.S_9b.i:
Find .
-
19M.2.SL.TZ2.S_9b.ii:
Given that all passengers for a flight arrive on time, find the probability that the flight does not depart on time.
-
19M.2.SL.TZ2.S_9c:
Find the value of .
-
19M.2.SL.TZ2.S_9d:
All flights have two pilots. Find the percentage of flights where both pilots flew more than 30 hours last week.
-
18N.2.SL.TZ0.S_9a:
A person is selected at random from Group X. Find the probability that their reaction time is greater than 0.65 seconds.
-
18N.2.SL.TZ0.S_9b:
The probability that the reaction time of a person in Group Y is greater than 0.65 seconds is 0.396. Find the value of σ.
-
18N.2.SL.TZ0.S_9c:
A randomly selected participant has a reaction time greater than 0.65 seconds. Find the probability that the participant is in Group X.
-
18N.2.SL.TZ0.S_9d:
Ten of the participants with reaction times greater than 0.65 are selected at random. Find the probability that at least two of them are in Group X.
-
17M.1.SL.TZ1.T_2a:
Calculate the percentage of the population of Ottawa that speak English but not French.
-
17M.1.SL.TZ1.T_2b:
Calculate the number of people in Ottawa that speak both English and French.
-
17M.1.SL.TZ1.T_2c:
Write down your answer to part (b) in the form where and k .
-
18M.2.SL.TZ1.T_2a:
State the alternative hypothesis.
-
18M.2.SL.TZ1.T_2b:
Calculate the expected frequency of flights travelling at most 500 km and arriving slightly delayed.
-
18M.2.SL.TZ1.T_2c:
Write down the number of degrees of freedom.
-
18M.2.SL.TZ1.T_2d.i:
Write down the χ2 statistic.
-
18M.2.SL.TZ1.T_2d.ii:
Write down the associated p-value.
-
18M.2.SL.TZ1.T_2e:
State, with a reason, whether you would reject the null hypothesis.
-
18M.2.SL.TZ1.T_2f:
Write down the probability that this flight arrived on time.
-
18M.2.SL.TZ1.T_2g:
Given that this flight was not heavily delayed, find the probability that it travelled between 500 km and 5000 km.
-
18M.2.SL.TZ1.T_2h:
Two flights are chosen at random from those which were slightly delayed.
Find the probability that each of these flights travelled at least 5000 km.
-
18M.1.SL.TZ2.T_7a:
State the number of boys who answered questions in Portuguese.
-
18M.1.SL.TZ2.T_7b:
Find the probability that the boy answered questions in Hindi.
-
18M.1.SL.TZ2.T_7c:
Two girls are selected at random.
Calculate the probability that one girl answered questions in Mandarin and the other answered questions in Hindi.
-
19M.1.SL.TZ1.T_5a:
Complete the cumulative frequency table.
-
19M.1.SL.TZ1.T_5b:
Write down the probability that a bouquet of roses sold is not small.
-
19M.1.SL.TZ1.T_5c:
A customer buys a large bouquet.
Find the probability that there are 12 roses in this bouquet.
-
17N.1.SL.TZ0.T_7a:
Complete the Venn diagram for these students.

-
17N.1.SL.TZ0.T_7b:
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.
-
17N.1.SL.TZ0.T_7c:
Determine whether the events and are independent.
-
18M.1.SL.TZ1.T_10b:
Find the value of x.
-
18M.1.SL.TZ2.T_9a.i:
Write down an expression, in set notation, for the shaded region represented by Diagram 1.
-
18M.1.SL.TZ2.T_9a.ii:
Write down an expression, in set notation, for the shaded region represented by Diagram 2.
-
18M.1.SL.TZ2.T_9a.iii:
Write down an expression, in set notation, for the shaded region represented by Diagram 3.
-
18M.1.SL.TZ2.T_9b.i:
Shade, on the Venn diagram, the region represented by the set .
-
18M.1.SL.TZ2.T_9b.ii:
Shade, on the Venn diagram, the region represented by the set .
-
18M.2.SL.TZ2.T_1a.i:
Write down the value of a.
-
18M.2.SL.TZ2.T_1a.ii:
Write down the value of b.
-
18M.2.SL.TZ2.T_1b.i:
Use the tree diagram to find the probability that an employee encountered traffic and was late for work.
-
18M.2.SL.TZ2.T_1b.ii:
Use the tree diagram to find the probability that an employee was late for work.
-
18M.2.SL.TZ2.T_1b.iii:
Use the tree diagram to find the probability that an employee encountered traffic given that they were late for work.
-
18M.2.SL.TZ2.T_1c.i:
Find the value of x.
-
18M.2.SL.TZ2.T_1c.ii:
Find the value of y.
-
18M.2.SL.TZ2.T_1d:
Find the number of employees who, in the last year, did not travel to work by car, bicycle or public transportation.
-
18M.2.SL.TZ2.T_1e:
Find .
-
17M.1.SL.TZ2.T_2a:
Write down an expression, in terms of , for the number of children who play only basketball.
-
17M.1.SL.TZ2.T_2b:
Complete the Venn diagram using the above information.
-
17M.1.SL.TZ2.T_2c:
Find the number of children who play only football.
-
17M.1.SL.TZ2.T_2d:
Write down the value of .
-
16N.1.SL.TZ0.T_3a:
In the table indicate whether the given statements are True or False.

-
16N.1.SL.TZ0.T_3b:
On the Venn diagram, shade the region .
-
17M.1.SL.TZ1.T_4a:
Write down the number of sporting activities offered by the school during its school year.
-
17M.1.SL.TZ1.T_4b:
Determine whether rock-climbing is offered by the school in the fall/autumn trimester.
-
17M.1.SL.TZ1.T_4c.i:
Write down the elements of the set ;
-
17M.1.SL.TZ1.T_4c.ii:
Write down .
-
17M.1.SL.TZ1.T_4d:
Write down, in terms of , and , an expression for the set which contains only archery, baseball, kayaking and surfing.
-
16N.2.SL.TZ0.T_2a:
Draw a Venn diagram to represent the given information, using sets labelled , and .
-
16N.2.SL.TZ0.T_2b:
Show that .
-
16N.2.SL.TZ0.T_2c:
Write down the value of .
-
16N.2.SL.TZ0.T_2d:
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.
-
18N.2.SL.TZ0.T_2a.i:
Find the number of students in the school that are taught in Spanish.
-
18N.2.SL.TZ0.T_2a.ii:
Find the number of students in the school that study Mathematics in English.
-
18N.2.SL.TZ0.T_2a.iii:
Find the number of students in the school that study both Biology and Mathematics.
-
18N.2.SL.TZ0.T_2b.i:
Write down .
-
18N.2.SL.TZ0.T_2b.ii:
Write down .
-
18N.2.SL.TZ0.T_2c.i:
Find the probability that this student studies Mathematics.
-
18N.2.SL.TZ0.T_2c.ii:
Find the probability that this student studies neither Biology nor Mathematics.
-
18N.2.SL.TZ0.T_2c.iii:
Find the probability that this student is taught in Spanish, given that the student studies Biology.
-
19M.1.SL.TZ2.T_5a:
Using the given information, complete the following Venn diagram.
-
19M.1.SL.TZ2.T_5b:
Find the number of surveyed students who did not like any of the three flavours.
-
19M.1.SL.TZ2.T_5c:
A student is chosen at random from the surveyed students.
Find the probability that this student likes kiwi fruit smoothies given that they like mango smoothies.
-
17N.2.SL.TZ0.T_4b:
Find the probability that both people chosen are not allergic to nuts.
-
17N.2.SL.TZ0.T_4c:
Copy and complete the tree diagram.
-
17N.2.SL.TZ0.T_4d:
Find the probability that this adult is allergic to nuts and the liquid turns blue.
-
17N.2.SL.TZ0.T_4e:
Find the probability that the liquid turns blue.
-
17N.2.SL.TZ0.T_4f:
Find the probability that the tested adult is allergic to nuts given that the liquid turned blue.
-
17N.2.SL.TZ0.T_4g:
Estimate the number of employees, from this 38, who are allergic to nuts.
-
18M.2.SL.TZ1.T_5a:
Write down the probability that Ayako avoids the trap in this wall.
-
18M.2.SL.TZ1.T_5b:
Find the probability that only one of Ayako and Natsuko falls into a trap while attempting to pass through a door in the first wall.
-
18M.2.SL.TZ1.T_5c:
Copy the probability tree diagram and write down the relevant probabilities along the branches.
-
18M.2.SL.TZ1.T_5d.i:
A contestant is chosen at random. Find the probability that this contestant fell into a trap while attempting to pass through a door in the second wall.
-
18M.2.SL.TZ1.T_5d.ii:
A contestant is chosen at random. Find the probability that this contestant fell into a trap.
-
18M.2.SL.TZ1.T_5e:
120 contestants attempted this game.
Find the expected number of contestants who fell into a trap while attempting to pass through a door in the third wall.
-
19M.2.SL.TZ2.T_1a:
Write down the null hypothesis, H0 , for this test.
-
19M.2.SL.TZ2.T_1b:
State the number of degrees of freedom.
-
19M.2.SL.TZ2.T_1c.i:
the expected frequency of female students who chose to take the Chinese class.
-
19M.2.SL.TZ2.T_1c.ii:
the statistic.
-
19M.2.SL.TZ2.T_1d:
State whether or not H0 should be rejected. Justify your statement.
-
19M.2.SL.TZ2.T_1e.i:
Find the probability that the student does not take the Spanish class.
-
19M.2.SL.TZ2.T_1e.ii:
Find the probability that neither of the two students take the Spanish class.
-
19M.2.SL.TZ2.T_1e.iii:
Find the probability that at least one of the two students is female.
-
19M.1.SL.TZ1.T_12a:
Find the probability that both spins are yellow.
-
19M.1.SL.TZ1.T_12b:
Find the probability that at least one of the spins is yellow.
-
19M.1.SL.TZ1.T_12c:
Write down the probability that the second spin is yellow, given that the first spin is blue.
-
17M.1.SL.TZ2.T_10a:
Write down the probability that a light bulb produced by Home Shine is not defective.
-
17M.1.SL.TZ2.T_10b.i:
Find the probability that both light bulbs are not defective.
-
17M.1.SL.TZ2.T_10b.ii:
Find the probability that at least one of Francesco’s light bulbs is defective.
-
17M.1.SL.TZ2.T_10c:
Write down an expression, in terms of , for the probability that at least one of Deborah’s three light bulbs is defective.
-
17M.1.SL.TZ1.T_7a:
Complete the tree diagram.
-
17M.1.SL.TZ1.T_7b:
Find the probability that Sara’s baggage arrives in London.
-
18N.1.SL.TZ0.T_8a:
Complete the tree diagram.
-
18N.1.SL.TZ0.T_8b:
Find the probability that Jorgé chooses a red disc.
-
16N.1.SL.TZ0.T_12a:
Complete the tree diagram below.

-
16N.1.SL.TZ0.T_12b:
Find the value of .
-
19N.1.SL.TZ0.S_2a:
Write down the value of .
-
19N.1.SL.TZ0.S_2b:
Find the value of .
-
19N.1.SL.TZ0.S_2c:
Write down the value of and of .
-
19N.2.SL.TZ0.S_9a:
Calculate the probability a flight is not late.
-
19N.2.SL.TZ0.S_9b:
Find the value of .
-
19N.2.SL.TZ0.S_9c.i:
Calculate the probability that at least of these flights are on time.
-
19N.2.SL.TZ0.S_9c.ii:
Given that at least of these flights are on time, find the probability that exactly flights are on time.
-
19N.2.SL.TZ0.S_9d:
SpeedWay increases the number of flights from city to city to flights each week, and improves their efficiency so that more flights are on time. The probability that at least flights are on time is .
A flight is chosen at random. Calculate the probability that it is on time.
-
20N.1.SL.TZ0.S_1a.i:
Find the value of .
-
20N.1.SL.TZ0.S_1a.ii:
Find the value of .
-
20N.1.SL.TZ0.S_1b:
Find the probability that a randomly selected student from the class plays tennis or volleyball, but not both.
-
20N.2.SL.TZ0.S_9a:
Find the probability that it will take Fiona between minutes and minutes to walk to the bus stop.
-
20N.2.SL.TZ0.S_9b:
Find .
-
20N.2.SL.TZ0.S_9c:
Find the probability that the bus journey takes less than minutes.
-
20N.2.SL.TZ0.S_9d:
Find the probability that Fiona will arrive on time.
-
20N.2.SL.TZ0.S_9e:
This year, Fiona will go to school on days.
Calculate the number of days Fiona is expected to arrive on time.
-
20N.1.SL.TZ0.T_14a:
Complete the values in the tree diagram.
-
20N.1.SL.TZ0.T_14b:
Find the value of .
-
20N.1.SL.TZ0.T_14c:
Given that Andre did not become the champion, find the probability that he lost in the semi-final.
-
20N.1.SL.TZ0.T_6a.i:
Find the probability that the first ball chosen is labelled .
-
20N.1.SL.TZ0.T_6a.ii:
Find the probability that the first ball chosen is labelled or labelled .
-
20N.1.SL.TZ0.T_6b:
Find the probability that the second ball chosen is labelled , given that the first ball chosen was labelled .
-
20N.1.SL.TZ0.T_6c:
Find the probability that both balls chosen are labelled .
-
20N.2.SL.TZ0.T_2a.i:
Find the value of .
-
20N.2.SL.TZ0.T_2a.ii:
Find the value of .
-
20N.2.SL.TZ0.T_2b:
Find the number of students who visited at least two types of main attraction.
-
20N.2.SL.TZ0.T_2c:
Write down the value of .
-
20N.2.SL.TZ0.T_2d.i:
Find the probability that a randomly selected student visited the rollercoasters.
-
20N.2.SL.TZ0.T_2d.ii:
Find the probability that a randomly selected student visited the virtual reality rides.
-
20N.2.SL.TZ0.T_2e:
Hence determine whether the events in parts (d)(i) and (d)(ii) are independent. Justify your reasoning.
-
EXN.2.AHL.TZ0.9:
A biased coin is weighted such that the probability, , of obtaining a tail is . The coin is tossed repeatedly and independently until a tail is obtained.
Let be the event “obtaining the first tail on an even numbered toss”.
Find .
-
21M.2.SL.TZ1.3c:
Given that a bag is not rejected, find the probability that it has a mass greater than grams.
-
21M.2.SL.TZ2.4a:
Find the probability that the student plays a sport and is involved in theatre.
-
21M.2.SL.TZ2.4b:
Find the probability that the student is involved in theatre, but does not play a sport.
-
21M.2.SL.TZ2.4c:
Find .
-
21M.2.SL.TZ2.4d:
Determine if the events and are independent. Justify your answer.
-
21N.1.SL.TZ0.4a:
A box is chosen at random and a ball is drawn. Find the probability that the ball is red.
-
21N.1.SL.TZ0.4b:
Let be the event that “box 1 is chosen” and let be the event that “a red ball is drawn”.
Determine whether events and are independent.
-
21N.2.SL.TZ0.4a:
Find the probability that there is at least one defective lamp in the sample.
-
21N.2.SL.TZ0.4b:
Given that there is at least one defective lamp in the sample, find the probability that there are at most two defective lamps.
-
21N.2.SL.TZ0.9a:
Find .
-
21N.2.SL.TZ0.9b:
Find the value of and of .
-
21N.2.SL.TZ0.9c.i:
medium.
-
21N.2.SL.TZ0.9c.ii:
large.
-
21N.2.SL.TZ0.9c.iii:
premium.
-
21N.2.SL.TZ0.9d:
The selling prices of the different categories of avocado at this supermarket are shown in the following table:
The supermarket pays the farm for the avocados and assumes it will then sell them in exactly the same proportion as purchased from the farm.
According to this model, find the minimum number of avocados that must be sold so that the net profit for the supermarket is at least .
-
22M.1.SL.TZ2.9c:
Assuming that rolls of the die are independent, find the probability that Nicky wins the game.
-
22M.2.SL.TZ1.6a:
Given that , find the value of .
-
22M.2.SL.TZ1.6b:
Find .
-
22M.2.SL.TZ1.9c.i:
Find the probability that the randomly selected muffin weighs less than .
-
22M.2.SL.TZ1.9c.ii:
Given that a randomly selected muffin weighs less than , find the probability that it is chocolate.
-
22M.2.SL.TZ2.4:
Events and are independent and .
Given that , find .
-
22M.2.SL.TZ2.9d:
Given that Suzi will be late to work at least one day next week, find the probability that she will be late less than three times.
-
22M.2.AHL.TZ2.8:
Rachel and Sophia are competing in a javelin-throwing competition.
The distances, metres, thrown by Rachel can be modelled by a normal distribution with mean and standard deviation .
The distances, metres, thrown by Sophia can be modelled by a normal distribution with mean and standard deviation .
In the first round of competition, each competitor must have five throws. To qualify for the next round of competition, a competitor must record at least one throw of metres or greater in the first round.
Find the probability that only one of Rachel or Sophia qualifies for the next round of competition.
SL 4.7—Discrete random variables
-
17M.1.SL.TZ1.S_10a:
Show that .
-
17M.1.SL.TZ1.S_10b:
Given that , find .
-
17M.1.SL.TZ1.S_10c:
Let , for . The graph of between and is rotated 360° about the -axis. Find the volume of the solid formed.
-
16N.2.AHL.TZ0.H_11a:
Show that and .
-
16N.2.AHL.TZ0.H_11b:
Find the values of the constants and .
-
16N.2.AHL.TZ0.H_11c:
Deduce that for .
-
16N.2.AHL.TZ0.H_11d:
(i) Hence show that has two modes and .
(ii) State the values of and .
-
16N.2.AHL.TZ0.H_11e:
Determine the minimum value of such that the probability Kati receives at least one free gift is greater than 0.5.
-
18M.1.AHL.TZ2.H_3a:
Find the value of p.
-
18M.1.AHL.TZ2.H_3b.i:
Find μ, the expected value of X.
-
18M.1.AHL.TZ2.H_3b.ii:
Find P(X > μ).
-
18M.1.AHL.TZ1.H_3a:
Find the value of a and the value of b.
-
18M.1.AHL.TZ1.H_3b:
Find the expected value of T.
-
19M.2.AHL.TZ2.H_10a:
Find the probability that on a randomly selected day, Steffi does not visit Will’s house.
-
19M.2.AHL.TZ2.H_10b:
Copy and complete the probability distribution table for Y.
-
19M.2.AHL.TZ2.H_10c:
Hence find the expected number of times per day that Steffi is fed at Will’s house.
-
19M.2.AHL.TZ2.H_10d:
In any given year of 365 days, the probability that Steffi does not visit Will for at most days in total is 0.5 (to one decimal place). Find the value of .
-
19M.2.AHL.TZ2.H_10e:
Show that the expected number of occasions per year on which Steffi visits Will’s house and is not fed is at least 30.
-
16N.1.AHL.TZ0.H_2a:
Complete the probability distribution table for .

-
16N.1.AHL.TZ0.H_2b:
Find the expected value of .
-
16N.2.AHL.TZ0.H_1a:
Determine the value of .
-
16N.2.AHL.TZ0.H_1b:
Find the value of .
-
17M.2.SL.TZ2.S_10a.i:
Find .
-
17M.2.SL.TZ2.S_10a.ii:
Find .
-
17M.2.SL.TZ2.S_10b.i:
Write down the probability of drawing three blue marbles.
-
17M.2.SL.TZ2.S_10b.ii:
Explain why the probability of drawing three white marbles is .
-
17M.2.SL.TZ2.S_10b.iii:
The bag contains a total of ten marbles of which are white. Find .
-
17M.2.SL.TZ2.S_10d:
Grant plays the game until he wins two prizes. Find the probability that he wins his second prize on his eighth attempt.
-
17M.2.SL.TZ2.S_10c:
Jill plays the game nine times. Find the probability that she wins exactly two prizes.
-
19M.2.SL.TZ1.S_10a.i:
Find the probability of rolling exactly one red face.
-
19M.2.SL.TZ1.S_10a.ii:
Find the probability of rolling two or more red faces.
-
19M.2.SL.TZ1.S_10b:
Show that, after a turn, the probability that Ted adds exactly $10 to his winnings is .
-
19M.2.SL.TZ1.S_10c.i:
Write down the value of .
-
19M.2.SL.TZ1.S_10c.ii:
Hence, find the value of .
-
19M.2.SL.TZ1.S_10d:
Ted will always have another turn if he expects an increase to his winnings.
Find the least value of for which Ted should end the game instead of having another turn.
-
18N.1.SL.TZ0.S_9a.i:
Find the probability, in terms of , that the game will end on her first draw.
-
18N.1.SL.TZ0.S_9a.ii:
Find the probability, in terms of , that the game will end on her second draw.
-
18N.1.SL.TZ0.S_9b.i:
third draw.
-
18N.1.SL.TZ0.S_9b.ii:
fourth draw.
-
18N.1.SL.TZ0.S_9c:
Hayley plays the game when = 5. She pays $20 to play and can earn money back depending on the number of draws it takes to obtain a blue marble. She earns no money back if she obtains a blue marble on her first draw. Let M be the amount of money that she earns back playing the game. This information is shown in the following table.
Find the value of so that this is a fair game.
-
17N.2.SL.TZ0.S_4a:
Find the value of .
-
17N.2.SL.TZ0.S_4b:
Write down .
-
17N.2.SL.TZ0.S_4c:
Find .
-
18M.2.SL.TZ1.S_2a:
Find the value of k.
-
18M.2.SL.TZ1.S_2b:
Calculate the expected value of the score.
-
18M.2.SL.TZ1.S_2c:
The die is rolled 80 times. On how many rolls would you expect to obtain a three?
-
18M.2.SL.TZ2.S_10a.i:
Write down the value of k.
-
18M.2.SL.TZ2.S_10a.ii:
Show that μ = 106.
-
18M.2.SL.TZ2.S_10b:
Find P(M < 95) .
-
18M.2.SL.TZ2.S_10c:
Find the probability that a bag of apples selected at random contains at most one small apple.
-
18M.2.SL.TZ2.S_10d.i:
Find the expected number of bags in this crate that contain at most one small apple.
-
18M.2.SL.TZ2.S_10d.ii:
Find the probability that at least 48 bags in this crate contain at most one small apple.
-
16N.2.SL.TZ0.S_7a:
Write down the probability that the first disc selected is red.
-
16N.2.SL.TZ0.S_7b:
Let be the number of red discs selected. Find the smallest value of for which .
-
19M.1.SL.TZ2.S_1a:
Find the value of .
-
19M.1.SL.TZ2.S_1b:
Find .
-
19N.1.AHL.TZ0.H_1a:
Find the value of .
-
19N.1.AHL.TZ0.H_1b:
Given that , find the value of .
-
19N.2.AHL.TZ0.H_10a:
Find, in terms of , the probability that lies between 1 and 3.
-
19N.2.AHL.TZ0.H_10b:
Sketch the graph of . State the coordinates of the end points and any local maximum or minimum points, giving your answers in terms of .
-
19N.2.AHL.TZ0.H_10c.i:
.
-
19N.2.AHL.TZ0.H_10c.ii:
.
-
19N.2.AHL.TZ0.H_10c.iii:
the median of .
-
19N.2.SL.TZ0.S_7a:
Show that .
-
19N.2.SL.TZ0.S_7b:
Find the difference between the greatest possible expected value and the least possible expected value.
-
20N.1.AHL.TZ0.H_1:
A discrete random variable has the probability distribution given by the following table.
Given that , determine the value of and the value of .
-
20N.2.SL.TZ0.S_3a:
Find an expression for in terms of .
-
20N.2.SL.TZ0.S_3b.i:
Find the value of which gives the largest value of .
-
20N.2.SL.TZ0.S_3b.ii:
Hence, find the largest value of .
-
EXN.1.SL.TZ0.3:
The following table shows the probability distribution of a discrete random variable where .
Find the value of , justifying your answer.
-
21M.1.SL.TZ1.9a:
Find the value of .
-
21M.1.SL.TZ1.9b:
Hence, find the value of .
-
21M.1.SL.TZ1.9c.i:
State the range of possible values of .
-
21M.1.SL.TZ1.9c.ii:
Hence, find the range of possible values of .
-
21M.1.SL.TZ1.9d:
Hence, find the range of possible values for .
-
21M.1.SL.TZ1.9e:
Agnes and Barbara play a game using these dice. Agnes rolls die once and Barbara rolls die once. The probability that Agnes’ score is less than Barbara’s score is .
Find the value of .
-
21M.2.SL.TZ2.9a:
Find the value of .
-
21M.2.SL.TZ2.9b:
Determine whether this lottery is a fair game in the first week. Justify your answer.
-
21M.2.SL.TZ2.9c:
Given that the grand prize is not won and the grand prize continues to double, write an expression in terms of for the value of the grand prize in the week of the lottery.
-
21M.2.SL.TZ2.9d:
The week is the first week in which the player is expected to make a profit. Ryan knows that if he buys a lottery ticket in the week, his expected profit is .
Find the value of .
-
21N.2.SL.TZ0.9a:
Find .
-
21N.2.SL.TZ0.9b:
Find the value of and of .
-
21N.2.SL.TZ0.9c.i:
medium.
-
21N.2.SL.TZ0.9c.ii:
large.
-
21N.2.SL.TZ0.9c.iii:
premium.
-
21N.2.SL.TZ0.9d:
The selling prices of the different categories of avocado at this supermarket are shown in the following table:
The supermarket pays the farm for the avocados and assumes it will then sell them in exactly the same proportion as purchased from the farm.
According to this model, find the minimum number of avocados that must be sold so that the net profit for the supermarket is at least .
-
22M.1.SL.TZ2.9a:
Show that and .
-
22M.1.SL.TZ2.9b:
Find .
-
22M.1.SL.TZ2.9d:
Determine the value of .
-
22M.1.SL.TZ2.9e:
Find the value of , providing evidence for your answer.
-
22M.2.SL.TZ1.4a:
Show that .
SL 4.8—Binomial distribution
-
SPM.2.SL.TZ0.4a:
The die is tossed five times. Find the probability of obtaining at most three “sixes”.
-
SPM.2.SL.TZ0.4b:
The die is tossed five times. Find the probability of obtaining the third “six” on the fifth toss.
-
SPM.2.SL.TZ0.8a:
Find P(24.15 < X < 25).
-
SPM.2.SL.TZ0.8b.i:
Find , the standard deviation of X.
-
SPM.2.SL.TZ0.8b.ii:
Hence, find the probability that a seashell selected at random has a length greater than 26 mm.
-
SPM.2.SL.TZ0.8c:
Find E(Y).
-
SPM.2.SL.TZ0.8d:
Find the probability that exactly three of these seashells have a length greater than 26 mm.
-
SPM.2.SL.TZ0.8e:
A seashell selected at random has a length less than 26 mm.
Find the probability that its length is between 24.15 mm and 25 mm.
-
17N.1.AHL.TZ0.H_10a:
Show that the probability that Chloe wins the game is .
-
17N.1.AHL.TZ0.H_10b.i:
Determine the mean of X.
-
17N.1.AHL.TZ0.H_10b.ii:
Determine the variance of X.
-
19M.2.AHL.TZ1.H_9a.i:
both a sandwich and a cake.
-
19M.2.AHL.TZ1.H_9a.ii:
only a sandwich.
-
19M.2.AHL.TZ1.H_9b.i:
Find the expected number of cakes sold on a typical day.
-
19M.2.AHL.TZ1.H_9b.ii:
Find the probability that more than 100 cakes will be sold on a typical day.
-
19M.2.AHL.TZ1.H_9c.i:
A customer is selected at random. Find the probability that the customer is male and buys a sandwich.
-
19M.2.AHL.TZ1.H_9c.ii:
A female customer is selected at random. Find the probability that she buys a sandwich.
-
18M.2.AHL.TZ1.H_6:
The mean number of squirrels in a certain area is known to be 3.2 squirrels per hectare of woodland. Within this area, there is a 56 hectare woodland nature reserve. It is known that there are currently at least 168 squirrels in this reserve.
Assuming the population of squirrels follow a Poisson distribution, calculate the probability that there are more than 190 squirrels in the reserve.
-
17M.2.AHL.TZ2.H_10a:
Show that and .
-
17M.2.AHL.TZ2.H_10b:
Find .
-
17M.2.AHL.TZ2.H_10c:
Find .
-
17M.2.AHL.TZ2.H_10d:
Find the median of .
-
17M.2.AHL.TZ2.H_10e:
Find .
-
17M.2.AHL.TZ2.H_10f:
Find .
-
19M.2.AHL.TZ2.H_10a:
Find the probability that on a randomly selected day, Steffi does not visit Will’s house.
-
19M.2.AHL.TZ2.H_10b:
Copy and complete the probability distribution table for Y.
-
19M.2.AHL.TZ2.H_10c:
Hence find the expected number of times per day that Steffi is fed at Will’s house.
-
19M.2.AHL.TZ2.H_10d:
In any given year of 365 days, the probability that Steffi does not visit Will for at most days in total is 0.5 (to one decimal place). Find the value of .
-
19M.2.AHL.TZ2.H_10e:
Show that the expected number of occasions per year on which Steffi visits Will’s house and is not fed is at least 30.
-
19M.2.AHL.TZ2.H_2a:
Calculate the probability that, on a randomly selected day, Timmy makes a profit.
-
19M.2.AHL.TZ2.H_2b:
The shop is open for 24 days every month.
Calculate the probability that, in a randomly selected month, Timmy makes a profit on between 5 and 10 days (inclusive).
-
18M.2.AHL.TZ2.H_8a:
Find the least possible value of n.
-
18M.2.AHL.TZ2.H_8b:
It is further given that P(X ≤ 1) = 0.09478 correct to 4 significant figures.
Determine the value of n and the value of p.
-
18M.2.AHL.TZ2.H_9a.i:
Find the probability that exactly 4 taxis arrive during T.
-
18M.2.AHL.TZ2.H_9a.ii:
Find the most likely number of taxis that would arrive during T.
-
18M.2.AHL.TZ2.H_9a.iii:
Given that more than 5 taxis arrive during T, find the probability that exactly 7 taxis arrive during T.
-
18M.2.AHL.TZ2.H_9b:
During quiet periods of the day, taxis arrive at a mean rate of 1.3 taxis every 10 minutes.
Find the probability that during a period of 15 minutes, of which the first 10 minutes is busy and the next 5 minutes is quiet, that exactly 2 taxis arrive.
-
16N.2.AHL.TZ0.H_3a:
Show that .
-
16N.2.AHL.TZ0.H_3b:
Given that and , use part (a) to find the value of .
-
17N.2.SL.TZ0.S_8a:
Write down the value of and of .
-
17N.2.SL.TZ0.S_8b:
Use this regression line to estimate the monthly honey production from a hive that has 270 bees.
-
17N.2.SL.TZ0.S_8c:
Write down the number of low production hives.
-
17N.2.SL.TZ0.S_8d.i:
Find the value of ;
-
17N.2.SL.TZ0.S_8d.ii:
Find the number of hives that have a high production.
-
17N.2.SL.TZ0.S_8e:
Adam decides to increase the number of bees in each low production hive. Research suggests that there is a probability of 0.75 that a low production hive becomes a regular production hive. Calculate the probability that 30 low production hives become regular production hives.
-
19M.2.SL.TZ1.S_10a.i:
Find the probability of rolling exactly one red face.
-
19M.2.SL.TZ1.S_10a.ii:
Find the probability of rolling two or more red faces.
-
19M.2.SL.TZ1.S_10b:
Show that, after a turn, the probability that Ted adds exactly $10 to his winnings is .
-
19M.2.SL.TZ1.S_10c.i:
Write down the value of .
-
19M.2.SL.TZ1.S_10c.ii:
Hence, find the value of .
-
19M.2.SL.TZ1.S_10d:
Ted will always have another turn if he expects an increase to his winnings.
Find the least value of for which Ted should end the game instead of having another turn.
-
18M.2.SL.TZ1.S_9a:
Find the probability that an orange weighs between 289 g and 310 g.
-
18M.2.SL.TZ1.S_9b.i:
Find the standardized value for 289 g.
-
18M.2.SL.TZ1.S_9b.ii:
Hence, find the value of σ.
-
18M.2.SL.TZ1.S_9c:
To the nearest gram, find the minimum weight of an orange that the grocer will buy.
-
18M.2.SL.TZ1.S_9d:
Find the probability that the grocer buys more than half the oranges in a box selected at random.
-
18M.2.SL.TZ1.S_9e:
The grocer selects two boxes at random.
Find the probability that the grocer buys more than half the oranges in each box.
-
18N.2.SL.TZ0.S_9a:
A person is selected at random from Group X. Find the probability that their reaction time is greater than 0.65 seconds.
-
18N.2.SL.TZ0.S_9b:
The probability that the reaction time of a person in Group Y is greater than 0.65 seconds is 0.396. Find the value of σ.
-
18N.2.SL.TZ0.S_9c:
A randomly selected participant has a reaction time greater than 0.65 seconds. Find the probability that the participant is in Group X.
-
18N.2.SL.TZ0.S_9d:
Ten of the participants with reaction times greater than 0.65 are selected at random. Find the probability that at least two of them are in Group X.
-
18M.2.SL.TZ2.S_10a.i:
Write down the value of k.
-
18M.2.SL.TZ2.S_10a.ii:
Show that μ = 106.
-
18M.2.SL.TZ2.S_10b:
Find P(M < 95) .
-
18M.2.SL.TZ2.S_10c:
Find the probability that a bag of apples selected at random contains at most one small apple.
-
18M.2.SL.TZ2.S_10d.i:
Find the expected number of bags in this crate that contain at most one small apple.
-
18M.2.SL.TZ2.S_10d.ii:
Find the probability that at least 48 bags in this crate contain at most one small apple.
-
17M.2.SL.TZ1.S_4a:
Find .
-
17M.2.SL.TZ1.S_4b.i:
Hence, find the probability that exactly students are left handed;
-
17M.2.SL.TZ1.S_4b.ii:
Hence, find the probability that fewer than students are left handed.
-
16N.2.SL.TZ0.S_7a:
Write down the probability that the first disc selected is red.
-
16N.2.SL.TZ0.S_7b:
Let be the number of red discs selected. Find the smallest value of for which .
-
19N.2.SL.TZ0.S_9a:
Calculate the probability a flight is not late.
-
19N.2.SL.TZ0.S_9b:
Find the value of .
-
19N.2.SL.TZ0.S_9c.i:
Calculate the probability that at least of these flights are on time.
-
19N.2.SL.TZ0.S_9c.ii:
Given that at least of these flights are on time, find the probability that exactly flights are on time.
-
19N.2.SL.TZ0.S_9d:
SpeedWay increases the number of flights from city to city to flights each week, and improves their efficiency so that more flights are on time. The probability that at least flights are on time is .
A flight is chosen at random. Calculate the probability that it is on time.
-
20N.2.SL.TZ0.T_6a:
Sketch a diagram to represent this information.
-
20N.2.SL.TZ0.T_6b:
Show that .
-
20N.2.SL.TZ0.T_6c.i:
Find the probability that Emlyn plays between and in a game.
-
20N.2.SL.TZ0.T_6c.ii:
Find the probability that Emlyn plays more than in a game.
-
20N.2.SL.TZ0.T_6d:
Find the value of .
-
20N.2.SL.TZ0.T_6e:
Find the probability he plays between and in one game and more than in the other game.
-
20N.2.SL.TZ0.T_6f:
Find the expected number of successful shots Emlyn will make on Monday, based on the results from Saturday and Sunday.
-
20N.2.SL.TZ0.T_6g:
Emlyn claims the results from Saturday and Sunday show that his expected number of successful shots will be more than Johan’s.
Determine if Emlyn’s claim is correct. Justify your reasoning.
-
EXN.2.SL.TZ0.8d:
Find the probability that at least five of them will take more than minutes to complete the jigsaw puzzle.
-
21M.2.SL.TZ2.8d:
Find the expected number of flights that will have a flight time of more than minutes.
-
21M.2.SL.TZ2.8e:
Find the probability that more than of the flights on this particular day will have a flight time of more than minutes.
-
21N.2.SL.TZ0.4a:
Find the probability that there is at least one defective lamp in the sample.
-
21N.2.SL.TZ0.4b:
Given that there is at least one defective lamp in the sample, find the probability that there are at most two defective lamps.
-
22M.2.SL.TZ1.9b:
In a random selection of chocolate muffins, find the probability that exactly weigh less than .
-
22M.2.SL.TZ2.9c:
Find the probability that she will be late to work at least one day next week.
-
22M.2.SL.TZ2.9d:
Given that Suzi will be late to work at least one day next week, find the probability that she will be late less than three times.
-
22M.2.SL.TZ2.9e:
Find the probability that Suzi will receive a bonus.
-
22M.2.AHL.TZ2.8:
Rachel and Sophia are competing in a javelin-throwing competition.
The distances, metres, thrown by Rachel can be modelled by a normal distribution with mean and standard deviation .
The distances, metres, thrown by Sophia can be modelled by a normal distribution with mean and standard deviation .
In the first round of competition, each competitor must have five throws. To qualify for the next round of competition, a competitor must record at least one throw of metres or greater in the first round.
Find the probability that only one of Rachel or Sophia qualifies for the next round of competition.
SL 4.9—Normal distribution and calculations
-
SPM.2.SL.TZ0.8a:
Find P(24.15 < X < 25).
-
SPM.2.SL.TZ0.8b.i:
Find , the standard deviation of X.
-
SPM.2.SL.TZ0.8b.ii:
Hence, find the probability that a seashell selected at random has a length greater than 26 mm.
-
SPM.2.SL.TZ0.8c:
Find E(Y).
-
SPM.2.SL.TZ0.8d:
Find the probability that exactly three of these seashells have a length greater than 26 mm.
-
SPM.2.SL.TZ0.8e:
A seashell selected at random has a length less than 26 mm.
Find the probability that its length is between 24.15 mm and 25 mm.
-
19M.2.AHL.TZ2.H_2a:
Calculate the probability that, on a randomly selected day, Timmy makes a profit.
-
19M.2.AHL.TZ2.H_2b:
The shop is open for 24 days every month.
Calculate the probability that, in a randomly selected month, Timmy makes a profit on between 5 and 10 days (inclusive).
-
17M.2.AHL.TZ2.H_3a:
Given that and find the probability that a randomly chosen packet of biscuits is underweight.
-
17M.2.AHL.TZ2.H_3b:
Calculate the new value of giving your answer correct to two decimal places.
-
17M.2.AHL.TZ2.H_3c:
Calculate the new value of .
-
18M.2.AHL.TZ1.H_4a:
Find the probability that a wolf selected at random is at least 5 years old.
-
18M.2.AHL.TZ1.H_4b:
Eight wolves are independently selected at random and their ages recorded.
Find the probability that more than six of these wolves are at least 5 years old.
-
18M.2.AHL.TZ2.H_3a:
Sketch the probability density function for X, and shade the region representing P(μ − 2σ < X < μ + σ).
-
18M.2.AHL.TZ2.H_3b:
Find the value of P(μ − 2σ < X < μ + σ).
-
18M.2.AHL.TZ2.H_3c:
Find the value of k for which P(μ − kσ < X < μ + kσ) = 0.5.
-
17M.2.AHL.TZ1.H_9a:
Find the probability that a runner selected at random will complete the marathon in less than 3 hours.
-
17M.2.AHL.TZ1.H_9b:
Calculate .
-
17M.2.AHL.TZ1.H_9c:
Find the standard deviation of the times taken by female runners.
-
18N.2.AHL.TZ0.H_3a:
Find the value of and the value of .
-
18N.2.AHL.TZ0.H_3b:
Find the probability that a randomly selected Infiglow battery will have a life of at least 15 hours.
-
19M.1.AHL.TZ1.H_6a:
.
-
19M.1.AHL.TZ1.H_6b:
.
-
16N.2.AHL.TZ0.H_8a:
Find and .
-
16N.2.AHL.TZ0.H_8b:
Find .
-
17N.2.AHL.TZ0.H_4:
It is given that one in five cups of coffee contain more than 120 mg of caffeine.
It is also known that three in five cups contain more than 110 mg of caffeine.Assume that the caffeine content of coffee is modelled by a normal distribution.
Find the mean and standard deviation of the caffeine content of coffee. -
18M.2.SL.TZ1.S_9a:
Find the probability that an orange weighs between 289 g and 310 g.
-
18M.2.SL.TZ1.S_9b.i:
Find the standardized value for 289 g.
-
18M.2.SL.TZ1.S_9b.ii:
Hence, find the value of σ.
-
18M.2.SL.TZ1.S_9c:
To the nearest gram, find the minimum weight of an orange that the grocer will buy.
-
18M.2.SL.TZ1.S_9d:
Find the probability that the grocer buys more than half the oranges in a box selected at random.
-
18M.2.SL.TZ1.S_9e:
The grocer selects two boxes at random.
Find the probability that the grocer buys more than half the oranges in each box.
-
17M.2.SL.TZ1.S_9a:
Find .
-
17M.2.SL.TZ1.S_9b:
Find the value of .
-
17M.2.SL.TZ1.S_9c:
Find .
-
17M.2.SL.TZ1.S_9d:
Given that , find .
-
19M.1.SL.TZ1.S_9a:
Find P(−1.6 < < 2.4). Write your answer in terms of and .
-
19M.1.SL.TZ1.S_9b:
Given that > −1.6, find the probability that z < 2.4 . Write your answer in terms of and .
-
19M.1.SL.TZ1.S_9c:
Write down the standardized value for .
-
19M.1.SL.TZ1.S_9d:
It is also known that P( > 2) = .
Find .
-
19M.2.SL.TZ2.S_9a:
Show that event A and event D are not independent.
-
19M.2.SL.TZ2.S_9b.i:
Find .
-
19M.2.SL.TZ2.S_9b.ii:
Given that all passengers for a flight arrive on time, find the probability that the flight does not depart on time.
-
19M.2.SL.TZ2.S_9c:
Find the value of .
-
19M.2.SL.TZ2.S_9d:
All flights have two pilots. Find the percentage of flights where both pilots flew more than 30 hours last week.
-
18N.2.SL.TZ0.S_9a:
A person is selected at random from Group X. Find the probability that their reaction time is greater than 0.65 seconds.
-
18N.2.SL.TZ0.S_9b:
The probability that the reaction time of a person in Group Y is greater than 0.65 seconds is 0.396. Find the value of σ.
-
18N.2.SL.TZ0.S_9c:
A randomly selected participant has a reaction time greater than 0.65 seconds. Find the probability that the participant is in Group X.
-
18N.2.SL.TZ0.S_9d:
Ten of the participants with reaction times greater than 0.65 are selected at random. Find the probability that at least two of them are in Group X.
-
18M.2.SL.TZ2.S_10a.i:
Write down the value of k.
-
18M.2.SL.TZ2.S_10a.ii:
Show that μ = 106.
-
18M.2.SL.TZ2.S_10b:
Find P(M < 95) .
-
18M.2.SL.TZ2.S_10c:
Find the probability that a bag of apples selected at random contains at most one small apple.
-
18M.2.SL.TZ2.S_10d.i:
Find the expected number of bags in this crate that contain at most one small apple.
-
18M.2.SL.TZ2.S_10d.ii:
Find the probability that at least 48 bags in this crate contain at most one small apple.
-
17M.1.SL.TZ2.S_3a:
Write down .
-
17M.1.SL.TZ2.S_3b:
Find .
-
17M.1.SL.TZ2.S_3c:
Find .
-
17N.2.SL.TZ0.S_7:
The heights of adult males in a country are normally distributed with a mean of 180 cm and a standard deviation of . 17% of these men are shorter than 168 cm. 80% of them have heights between and 192 cm.
Find the value of .
-
16N.2.SL.TZ0.S_5a:
Given that 5.3% of newborn babies have a low birth weight, find .
-
17M.2.SL.TZ1.T_5a.i:
Calculate the mean test grade of the students;
-
17M.2.SL.TZ1.T_5a.ii:
Calculate the standard deviation.
-
17M.2.SL.TZ1.T_5b:
Find the median test grade of the students.
-
17M.2.SL.TZ1.T_5c:
Find the interquartile range.
-
17M.2.SL.TZ1.T_5d:
Find the probability that this student scored a grade 5 or higher.
-
17M.2.SL.TZ1.T_5e:
Given that the first student chosen at random scored a grade 5 or higher, find the probability that both students scored a grade 6.
-
17M.2.SL.TZ1.T_5f.i:
Calculate the probability that a student chosen at random spent at least 90 minutes preparing for the test.
-
17M.2.SL.TZ1.T_5f.ii:
Calculate the expected number of students that spent at least 90 minutes preparing for the test.
-
19M.1.SL.TZ2.T_14a.ii:
Find the price that is two standard deviations above the mean price.
-
19M.1.SL.TZ2.T_14b:
Find the probability that the price of a kilogram of tomatoes, chosen at random, will be between 2.00 and 3.00 euro.
-
19M.1.SL.TZ2.T_14c:
To stimulate reasonable pricing, the city offers a free permit to the sellers whose price of a kilogram of tomatoes is in the lowest 20 %.
Find the highest price that a seller can charge and still receive a free permit.
-
18M.1.SL.TZ1.T_13a.i:
Find the probability that a student, chosen at random arrives at least 60 minutes after the school opens.
-
18M.1.SL.TZ1.T_13a.ii:
Find the probability that a student, chosen at random arrives between 45 minutes and 55 minutes after the school opens.
-
18M.1.SL.TZ1.T_13b:
A second school, Mulberry Park, also opens at 08:00 every morning. The arrival times of the students at this school follows exactly the same distribution as Malthouse school.
Given that, on one morning, 15 students arrive at least 60 minutes after the school opens, estimate the number of students at Mulberry Park school.
-
17N.1.SL.TZ0.T_13a:
Find the probability that this applicant took at least 40 minutes to complete the test.
-
17N.1.SL.TZ0.T_13b:
Find the value of .
-
17N.1.SL.TZ0.T_13c:
Estimate the number of applicants who completed the test in less than 25 minutes.
-
17M.1.SL.TZ2.T_11a:
Write down the probability that the mass of one of these corncobs is greater than 400 grams.
-
17M.1.SL.TZ2.T_11b:
Find the value of .
-
17M.1.SL.TZ2.T_11c:
Estimate the interquartile range of the distribution.
-
16N.2.SL.TZ0.T_4a:
Draw a diagram that shows this information.
-
16N.2.SL.TZ0.T_4b:
(i) Find the probability that a box of cereal, chosen at random, is sold.
(ii) Calculate the manufacturer’s expected daily income from these sales.
-
16N.2.SL.TZ0.T_4c:
Calculate the manufacturer’s expected daily recycling cost.
-
16N.2.SL.TZ0.T_4d:
Calculate the value of .
-
18M.2.SL.TZ2.T_3a.i:
Find the probability that a basketball player has a weight that is less than 61 kg.
-
18M.2.SL.TZ2.T_3a.ii:
In a training session there are 40 basketball players.
Find the expected number of players with a weight less than 61 kg in this training session.
-
18M.2.SL.TZ2.T_3b.i:
Sketch a normal curve to represent this probability.
-
18M.2.SL.TZ2.T_3b.ii:
Find the value of q.
-
18M.2.SL.TZ2.T_3c:
Given that P(W > k) = 0.225 , find the value of k.
-
18M.2.SL.TZ2.T_3d.i:
For this test state the null hypothesis.
-
18M.2.SL.TZ2.T_3d.ii:
For this test find the p-value.
-
18M.2.SL.TZ2.T_3e:
State a conclusion for this test. Justify your answer.
-
19M.1.SL.TZ1.T_11a:
In the following table, write down the letter of the corresponding graph next to the given mean and standard deviation.
-
19M.1.SL.TZ1.T_11b:
Find the probability that a suitcase weighs less than 15 kg.
-
19M.1.SL.TZ1.T_11c:
Any suitcase that weighs more than kg is identified as excess baggage.
19.6 % of the suitcases at this airport are identified as excess baggage.Find the value of .
-
19N.2.AHL.TZ0.H_7:
Runners in an athletics club have season’s best times for the 100 m, which can be modelled by a normal distribution with mean 11.6 seconds and standard deviation 0.8 seconds. To qualify for a particular competition a runner must have a season’s best time of under 11 seconds. A runner from this club who has qualified for the competition is selected at random. Find the probability that he has a season’s best time of under 10.7 seconds.
-
19N.1.SL.TZ0.S_7a:
Find so that .
-
19N.1.SL.TZ0.S_7b:
It is given that .
Find .
-
19N.2.SL.TZ0.S_9a:
Calculate the probability a flight is not late.
-
19N.2.SL.TZ0.S_9b:
Find the value of .
-
19N.2.SL.TZ0.S_9c.i:
Calculate the probability that at least of these flights are on time.
-
19N.2.SL.TZ0.S_9c.ii:
Given that at least of these flights are on time, find the probability that exactly flights are on time.
-
19N.2.SL.TZ0.S_9d:
SpeedWay increases the number of flights from city to city to flights each week, and improves their efficiency so that more flights are on time. The probability that at least flights are on time is .
A flight is chosen at random. Calculate the probability that it is on time.
-
20N.2.AHL.TZ0.H_9a:
Find the probability that a randomly selected packet has a weight less than .
-
20N.2.AHL.TZ0.H_9b:
The probability that a randomly selected packet has a weight greater than grams is . Find the value of .
-
20N.2.AHL.TZ0.H_9c:
A packet is randomly selected. Given that the packet has a weight greater than , find the probability that it has a weight greater than .
-
20N.2.AHL.TZ0.H_9d:
From a random sample of packets, determine the number of packets that would be expected to have a weight lying within standard deviations of the mean.
-
20N.2.AHL.TZ0.H_9e:
Packets are delivered to supermarkets in batches of . Determine the probability that at least packets from a randomly selected batch have a weight less than .
-
20N.2.SL.TZ0.T_6a:
Sketch a diagram to represent this information.
-
20N.2.SL.TZ0.T_6b:
Show that .
-
20N.2.SL.TZ0.T_6c.i:
Find the probability that Emlyn plays between and in a game.
-
20N.2.SL.TZ0.T_6c.ii:
Find the probability that Emlyn plays more than in a game.
-
20N.2.SL.TZ0.T_6d:
Find the value of .
-
20N.2.SL.TZ0.T_6e:
Find the probability he plays between and in one game and more than in the other game.
-
20N.2.SL.TZ0.T_6f:
Find the expected number of successful shots Emlyn will make on Monday, based on the results from Saturday and Sunday.
-
20N.2.SL.TZ0.T_6g:
Emlyn claims the results from Saturday and Sunday show that his expected number of successful shots will be more than Johan’s.
Determine if Emlyn’s claim is correct. Justify your reasoning.
-
EXN.2.SL.TZ0.8a:
By stating and solving an appropriate equation, show, correct to two decimal places, that .
-
EXN.2.SL.TZ0.8b:
Find the th percentile time to complete the jigsaw puzzle.
-
EXN.2.SL.TZ0.8c:
Find the probability that a randomly chosen person will take more than minutes to complete the jigsaw puzzle.
-
21M.2.SL.TZ1.3a:
Find the probability that a bag selected at random is rejected.
-
21M.2.SL.TZ1.3b:
Estimate the number of bags which will be rejected from a random sample of bags.
-
21M.2.SL.TZ1.3c:
Given that a bag is not rejected, find the probability that it has a mass greater than grams.
-
21M.2.SL.TZ2.8a:
Given that of the flight times are longer than minutes, find the value of .
-
21M.2.SL.TZ2.8b:
Find the probability that a randomly selected flight will have a flight time of more than minutes.
-
21M.2.SL.TZ2.8c:
Given that a flight between the two cities takes longer than minutes, find the probability that it takes less than minutes.
-
21M.2.SL.TZ2.8d:
Find the expected number of flights that will have a flight time of more than minutes.
-
21M.2.SL.TZ2.8e:
Find the probability that more than of the flights on this particular day will have a flight time of more than minutes.
-
22M.2.SL.TZ1.9a:
Find the probability that a randomly selected chocolate muffin weighs less than .
-
22M.2.SL.TZ1.9c.i:
Find the probability that the randomly selected muffin weighs less than .
-
22M.2.SL.TZ2.9b:
On a randomly selected day, find the probability that Suzi’s drive to work will take longer than minutes.
-
22M.2.AHL.TZ2.8:
Rachel and Sophia are competing in a javelin-throwing competition.
The distances, metres, thrown by Rachel can be modelled by a normal distribution with mean and standard deviation .
The distances, metres, thrown by Sophia can be modelled by a normal distribution with mean and standard deviation .
In the first round of competition, each competitor must have five throws. To qualify for the next round of competition, a competitor must record at least one throw of metres or greater in the first round.
Find the probability that only one of Rachel or Sophia qualifies for the next round of competition.
SL 4.10—X on y regression line
-
SPM.2.SL.TZ0.5a:
Find the value of a and the value of b.
-
SPM.2.SL.TZ0.5b:
Let L2 be the regression line of y on x. The lines L1 and L2 pass through the same point with coordinates (p , q).
Find the value of p and the value of q.
-
SPM.2.AHL.TZ0.4a:
Find the value of a and the value of b.
-
SPM.2.AHL.TZ0.4b:
Find the value of p and the value of q.
-
SPM.2.AHL.TZ0.4c:
Jennifer was absent for the first test but scored 29 marks on the second test. Use an appropriate regression equation to estimate Jennifer’s mark on the first test.
-
EXM.2.SL.TZ0.1a:
State the name for this type of sampling technique.
-
EXM.2.SL.TZ0.1b.i:
Show that 3 students will be selected from grade 12.
-
EXM.2.SL.TZ0.1b.ii:
Calculate the number of students in each grade in the sample.
-
EXM.2.SL.TZ0.1c:
State the name for this type of sampling technique.
-
EXM.2.SL.TZ0.1d.i:
Calculate Pearson’s product moment correlation coefficient, .
-
EXM.2.SL.TZ0.1d.ii:
Interpret the meaning of the value of in the context of the principal’s concerns.
-
EXM.2.SL.TZ0.1d.iii:
Explain why the value of makes it appropriate to find the equation of a regression line.
-
EXM.2.SL.TZ0.1e:
Another student at the school, Jasmine, has a self-esteem value of 29.
By finding the equation of an appropriate regression line, estimate the time Jasmine spent on social media the previous day.
-
19N.3.AHL.TZ0.Hsp_1a.i:
State suitable hypotheses and to test Peter’s claim, using a two-tailed test.
-
19N.3.AHL.TZ0.Hsp_1a.ii:
Carry out a suitable test at the 5 % significance level. With reference to the -value, state your conclusion in the context of Peter’s claim.
-
19N.3.AHL.TZ0.Hsp_1b:
Peter uses the regression line of on as and calculates that a student with a Mathematics test score of 73 will have a running time of 101 seconds. Comment on the validity of his calculation.
-
22M.1.SL.TZ1.3b.i:
One of the adults surveyed is years old. Estimate the age of their eldest child.
-
22M.1.SL.TZ1.3b.ii:
Find the mean age of all the adults surveyed.
SL 4.11—Conditional and independent probabilities, test for independence
-
SPM.1.SL.TZ0.2:
Let A and B be events such that , and .
Find .
-
EXN.2.SL.TZ0.8e:
Having spent minutes attempting the jigsaw puzzle, a randomly chosen person had not yet completed the puzzle.
Find the probability that this person will take more than minutes to complete the jigsaw puzzle.
-
21M.2.SL.TZ2.8c:
Given that a flight between the two cities takes longer than minutes, find the probability that it takes less than minutes.
-
21N.1.SL.TZ0.4a:
A box is chosen at random and a ball is drawn. Find the probability that the ball is red.
-
21N.1.SL.TZ0.4b:
Let be the event that “box 1 is chosen” and let be the event that “a red ball is drawn”.
Determine whether events and are independent.
-
22M.2.SL.TZ1.6a:
Given that , find the value of .
-
22M.2.SL.TZ1.6b:
Find .
-
22M.2.SL.TZ1.9c.ii:
Given that a randomly selected muffin weighs less than , find the probability that it is chocolate.
SL 4.12—Z values, inverse normal to find mean and standard deviation
-
19M.2.AHL.TZ2.H_2a:
Calculate the probability that, on a randomly selected day, Timmy makes a profit.
-
19M.2.AHL.TZ2.H_2b:
The shop is open for 24 days every month.
Calculate the probability that, in a randomly selected month, Timmy makes a profit on between 5 and 10 days (inclusive).
-
17M.2.AHL.TZ2.H_3a:
Given that and find the probability that a randomly chosen packet of biscuits is underweight.
-
17M.2.AHL.TZ2.H_3b:
Calculate the new value of giving your answer correct to two decimal places.
-
17M.2.AHL.TZ2.H_3c:
Calculate the new value of .
-
18M.2.AHL.TZ1.H_4a:
Find the probability that a wolf selected at random is at least 5 years old.
-
18M.2.AHL.TZ1.H_4b:
Eight wolves are independently selected at random and their ages recorded.
Find the probability that more than six of these wolves are at least 5 years old.
-
18M.2.AHL.TZ2.H_3a:
Sketch the probability density function for X, and shade the region representing P(μ − 2σ < X < μ + σ).
-
18M.2.AHL.TZ2.H_3b:
Find the value of P(μ − 2σ < X < μ + σ).
-
18M.2.AHL.TZ2.H_3c:
Find the value of k for which P(μ − kσ < X < μ + kσ) = 0.5.
-
17M.2.AHL.TZ1.H_9a:
Find the probability that a runner selected at random will complete the marathon in less than 3 hours.
-
17M.2.AHL.TZ1.H_9b:
Calculate .
-
17M.2.AHL.TZ1.H_9c:
Find the standard deviation of the times taken by female runners.
-
18N.2.AHL.TZ0.H_3a:
Find the value of and the value of .
-
18N.2.AHL.TZ0.H_3b:
Find the probability that a randomly selected Infiglow battery will have a life of at least 15 hours.
-
19M.1.AHL.TZ1.H_6a:
.
-
19M.1.AHL.TZ1.H_6b:
.
-
16N.2.AHL.TZ0.H_8a:
Find and .
-
16N.2.AHL.TZ0.H_8b:
Find .
-
17N.2.AHL.TZ0.H_4:
It is given that one in five cups of coffee contain more than 120 mg of caffeine.
It is also known that three in five cups contain more than 110 mg of caffeine.Assume that the caffeine content of coffee is modelled by a normal distribution.
Find the mean and standard deviation of the caffeine content of coffee. -
20N.2.SL.TZ0.S_9a:
Find the probability that it will take Fiona between minutes and minutes to walk to the bus stop.
-
20N.2.SL.TZ0.S_9b:
Find .
-
20N.2.SL.TZ0.S_9c:
Find the probability that the bus journey takes less than minutes.
-
20N.2.SL.TZ0.S_9d:
Find the probability that Fiona will arrive on time.
-
20N.2.SL.TZ0.S_9e:
This year, Fiona will go to school on days.
Calculate the number of days Fiona is expected to arrive on time.
-
EXN.2.SL.TZ0.8a:
By stating and solving an appropriate equation, show, correct to two decimal places, that .
-
EXN.2.SL.TZ0.8b:
Find the th percentile time to complete the jigsaw puzzle.
-
EXN.2.SL.TZ0.8c:
Find the probability that a randomly chosen person will take more than minutes to complete the jigsaw puzzle.
-
21M.2.SL.TZ2.8a:
Given that of the flight times are longer than minutes, find the value of .
-
21M.2.SL.TZ2.8b:
Find the probability that a randomly selected flight will have a flight time of more than minutes.
-
21M.2.SL.TZ2.8c:
Given that a flight between the two cities takes longer than minutes, find the probability that it takes less than minutes.
-
21M.2.SL.TZ2.8d:
Find the expected number of flights that will have a flight time of more than minutes.
-
21M.2.SL.TZ2.8e:
Find the probability that more than of the flights on this particular day will have a flight time of more than minutes.
-
21N.2.SL.TZ0.9a:
Find .
-
21N.2.SL.TZ0.9b:
Find the value of and of .
-
21N.2.SL.TZ0.9c.i:
medium.
-
21N.2.SL.TZ0.9c.ii:
large.
-
21N.2.SL.TZ0.9c.iii:
premium.
-
21N.2.SL.TZ0.9d:
The selling prices of the different categories of avocado at this supermarket are shown in the following table:
The supermarket pays the farm for the avocados and assumes it will then sell them in exactly the same proportion as purchased from the farm.
According to this model, find the minimum number of avocados that must be sold so that the net profit for the supermarket is at least .
-
22M.2.SL.TZ1.9d:
Find the value of .
-
22M.2.SL.TZ2.9a:
Find the value of .
AHL 4.13—Bayes theorem
NoneAHL 4.14—Properties of discrete and continuous random variables
-
SPM.1.AHL.TZ0.7:
A continuous random variable X has the probability density function given by
.
Find P(0 ≤ X ≤ 3).
-
SPM.2.AHL.TZ0.6a:
Find E(T).
-
SPM.2.AHL.TZ0.6b:
Given that Var(X) = 0.8419, find Var(T).
-
19M.1.AHL.TZ2.H_10a:
State the mode of .
-
19M.1.AHL.TZ2.H_10b.i:
Find .
-
19M.1.AHL.TZ2.H_10b.ii:
Hence show that .
-
19M.1.AHL.TZ2.H_10c.i:
.
-
19M.1.AHL.TZ2.H_10c.ii:
.
-
17M.1.AHL.TZ1.H_10a:
Find the value of .
-
17M.1.AHL.TZ1.H_10b.i:
By considering the graph of f write down the mean of ;
-
17M.1.AHL.TZ1.H_10b.ii:
By considering the graph of f write down the median of ;
-
17M.1.AHL.TZ1.H_10b.iii:
By considering the graph of f write down the mode of .
-
17M.1.AHL.TZ1.H_10c.i:
Show that .
-
17M.1.AHL.TZ1.H_10c.ii:
Hence state the interquartile range of .
-
17M.1.AHL.TZ1.H_10d:
Calculate .
-
18M.1.AHL.TZ1.H_3a:
Find the value of a and the value of b.
-
18M.1.AHL.TZ1.H_3b:
Find the expected value of T.
-
18M.2.AHL.TZ1.H_10a:
Show that .
-
18M.2.AHL.TZ1.H_10b:
Find .
-
18M.2.AHL.TZ1.H_10c:
Given that , and that 0.25 < s < 0.4 , find the value of s.
-
17M.2.AHL.TZ2.H_10a:
Show that and .
-
17M.2.AHL.TZ2.H_10b:
Find .
-
17M.2.AHL.TZ2.H_10c:
Find .
-
17M.2.AHL.TZ2.H_10d:
Find the median of .
-
17M.2.AHL.TZ2.H_10e:
Find .
-
17M.2.AHL.TZ2.H_10f:
Find .
-
19M.2.AHL.TZ2.H_10a:
Find the probability that on a randomly selected day, Steffi does not visit Will’s house.
-
19M.2.AHL.TZ2.H_10b:
Copy and complete the probability distribution table for Y.
-
19M.2.AHL.TZ2.H_10c:
Hence find the expected number of times per day that Steffi is fed at Will’s house.
-
19M.2.AHL.TZ2.H_10d:
In any given year of 365 days, the probability that Steffi does not visit Will for at most days in total is 0.5 (to one decimal place). Find the value of .
-
19M.2.AHL.TZ2.H_10e:
Show that the expected number of occasions per year on which Steffi visits Will’s house and is not fed is at least 30.
-
16N.1.AHL.TZ0.H_2a:
Complete the probability distribution table for .

-
16N.1.AHL.TZ0.H_2b:
Find the expected value of .
-
16N.2.AHL.TZ0.H_1a:
Determine the value of .
-
16N.2.AHL.TZ0.H_1b:
Find the value of .
-
17M.2.SL.TZ2.S_10a.i:
Find .
-
19N.1.AHL.TZ0.H_1a:
Find the value of .
-
19N.1.AHL.TZ0.H_1b:
Given that , find the value of .
-
20N.1.AHL.TZ0.H_1:
A discrete random variable has the probability distribution given by the following table.
Given that , determine the value of and the value of .
-
21M.2.AHL.TZ1.7a:
Show that .
-
21M.2.AHL.TZ2.6a:
Show that .
-
21M.2.AHL.TZ2.6b:
Show that .
-
21N.2.AHL.TZ0.7a:
Determine the value of .
-
21N.2.AHL.TZ0.7b:
Given that , determine the value of .
-
22M.1.AHL.TZ1.7a:
Find the value of .
-
22M.1.AHL.TZ1.7b:
Find .
-
22M.1.AHL.TZ2.8:
A continuous random variable has the probability density function
.
The following diagram shows the graph of for .
Given that , find an expression for the median of in terms of and .
