| Date | November 2017 | Marks available | 2 | Reference code | 17N.2.SL.TZ0.T_1 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | State | Question number | T_1 | Adapted from | N/A |
Question
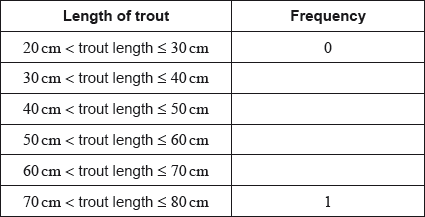
A group of 800 students answered 40 questions on a category of their choice out of History, Science and Literature.
For each student the category and the number of correct answers, , was recorded. The results obtained are represented in the following table.
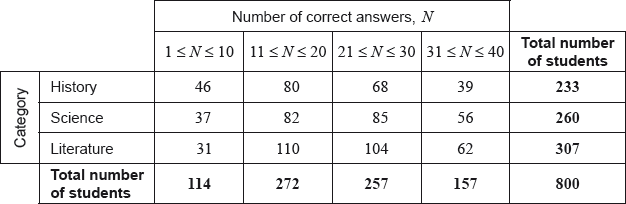
A test at the 5% significance level is carried out on the results. The critical value for this test is 12.592.
State whether is a discrete or a continuous variable.
Write down, for , the modal class;
Write down, for , the mid-interval value of the modal class.
Use your graphic display calculator to estimate the mean of ;
Use your graphic display calculator to estimate the standard deviation of .
Find the expected frequency of students choosing the Science category and obtaining 31 to 40 correct answers.
Write down the null hypothesis for this test;
Write down the number of degrees of freedom.
Write down the -value for the test;
Write down the statistic.
State the result of the test. Give a reason for your answer.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
discrete (A1)
[1 mark]
(A1)
[1 mark]
15.5 (A1)(ft)
Note: Follow through from part (b)(i).
[1 mark]
(G2)
[2 marks]
(G1)
[1 marks]
OR (M1)
Note: Award (M1) for correct substitution into expected frequency formula.
(A1)(G2)
[2 marks]
choice of category and number of correct answers are independent (A1)
Notes: Accept “no association” between (choice of) category and number of correct answers. Do not accept “not related” or “not correlated” or “influenced”.
[1 mark]
6 (A1)
[1 mark]
(G1)
[1 mark]
(G2)
[2 marks]
the null hypothesis is not rejected (the null hypothesis is accepted) (A1)(ft)
OR
(choice of) category and number of correct answers are independent (A1)(ft)
as OR (R1)
Notes: Award (R1) for a correct comparison of either their statistic to the critical value or their -value to the significance level. Award (A1)(ft) from that comparison.
Follow through from part (f). Do not award (A1)(ft)(R0).
[2 marks]