| Date | May 2019 | Marks available | 2 | Reference code | 19M.1.SL.TZ1.T_12 |
| Level | Standard Level | Paper | Paper 1 (with calculator from previous syllabus) | Time zone | Time zone 1 |
| Command term | Find | Question number | T_12 | Adapted from | N/A |
Question
The diagram shows a circular horizontal board divided into six equal sectors. The sectors are labelled white (W), yellow (Y) and blue (B).
A pointer is pinned to the centre of the board. The pointer is to be spun and when it stops the colour of the sector on which the pointer stops is recorded. The pointer is equally likely to stop on any of the six sectors.
Eva will spin the pointer twice. The following tree diagram shows all the possible outcomes.
Find the probability that both spins are yellow.
Find the probability that at least one of the spins is yellow.
Write down the probability that the second spin is yellow, given that the first spin is blue.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
OR (M1)
Note: Award (M1) for multiplying correct probabilities.
(0.111, 0.111111…, 11.1%) (A1) (C2)
[2 marks]
(M1)(M1)
Note: Award (M1) for and or equivalent, and (M1) for and adding only the three correct probabilities.
OR
(M1)(M1)
Note: Award (M1) for seen and (M1) for subtracting from 1. This may be shown in a tree diagram with “yellow” and “not yellow” branches.
(0.556, 0.555555…, 55.6%) (A1)(ft) (C3)
Note: Follow through marks may be awarded if their answer to part (a) is used in a correct calculation.
[3 marks]
(0.333, 0.333333…, 33.3%) (A1) (C1)
[1 mark]
Examiners report
Syllabus sections
-
18M.2.SL.TZ1.S_4a:
Write down the coordinates of the vertex of the graph of g.
-
18M.2.SL.TZ2.S_9a:
Find the initial velocity of P.
-
18M.2.SL.TZ2.S_9d:
Find the acceleration of P when it changes direction.
-
19M.1.SL.TZ1.S_7b:
Find the total distance travelled in the first 5 seconds.
-
19M.2.SL.TZ2.S_8c:
Find the value of when particle A first changes direction.
-
19M.1.AHL.TZ1.H_8d:
Sketch the curve , 0 ≤ ≤ 5 indicating clearly the coordinates of the maximum and minimum points and any intercepts with the coordinate axes.
-
18M.2.SL.TZ1.S_4b:
On the grid above, sketch the graph of g for −2 ≤ x ≤ 4.
-
21N.1.SL.TZ0.7b:
Sketch a graph of against , clearly showing any points of intersection with the axes.
-
18M.3.AHL.TZ0.Hca_3c:
Hence write down a lower bound for .
-
18M.2.SL.TZ1.T_2a:
State the alternative hypothesis.
-
18M.2.SL.TZ1.T_2d.i:
Write down the χ2 statistic.
-
18M.2.SL.TZ1.T_2d.ii:
Write down the associated p-value.
-
18M.2.SL.TZ2.T_1c.i:
Find the value of x.
-
18M.2.SL.TZ1.T_5c:
Copy the probability tree diagram and write down the relevant probabilities along the branches.
-
18M.2.SL.TZ1.T_5e:
120 contestants attempted this game.
Find the expected number of contestants who fell into a trap while attempting to pass through a door in the third wall.
-
19M.2.SL.TZ2.T_1c.i:
the expected frequency of female students who chose to take the Chinese class.
-
16N.2.SL.TZ0.S_9b:
Find the value of .
-
17M.2.SL.TZ1.S_7a.i:
Write down the first value of at which P changes direction.
-
17M.2.SL.TZ1.S_7a.ii:
Find the total distance travelled by P, for .
-
18M.2.SL.TZ1.T_5a:
Write down the probability that Ayako avoids the trap in this wall.
-
17N.2.SL.TZ0.S_9b:
Hence or otherwise, find all possible values of for which the velocity of P is decreasing.
-
17N.1.SL.TZ0.T_7a:
Complete the Venn diagram for these students.
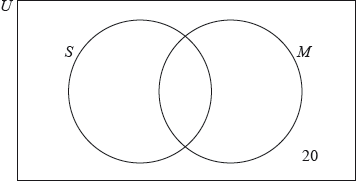
-
19M.1.SL.TZ2.T_5a:
Using the given information, complete the following Venn diagram.
-
18N.2.SL.TZ0.T_2b.i:
Write down .
-
18N.2.SL.TZ0.T_2b.ii:
Write down .
-
18M.2.SL.TZ2.S_9e:
Find the total distance travelled by P.
-
SPM.2.AHL.TZ0.11a:
Show that + 1 is an integrating factor for this differential equation.
-
18M.2.SL.TZ2.T_1c.ii:
Find the value of y.
-
17M.2.SL.TZ1.S_10b.i:
Find .
-
19N.1.SL.TZ0.S_8a:
Write down an expression for in terms of .
-
SPM.2.AHL.TZ0.11d:
Find the value of at which the amount of salt in the tank is decreasing most rapidly.
-
19N.1.SL.TZ0.S_8d.i:
Find the value of for which is a maximum.
-
17M.1.SL.TZ1.S_10b:
Given that , find .
-
19M.2.SL.TZ2.S_8d:
Find the total distance travelled by particle A in the first 3 seconds.
-
19M.2.SL.TZ2.T_1e.iii:
Find the probability that at least one of the two students is female.
-
19M.2.SL.TZ2.T_1c.ii:
the statistic.
-
17N.2.SL.TZ0.T_4g:
Estimate the number of employees, from this 38, who are allergic to nuts.
-
19M.2.SL.TZ2.T_1a:
Write down the null hypothesis, H0 , for this test.
-
16N.2.SL.TZ0.S_9a:
Find the initial velocity of .
-
18M.2.SL.TZ2.T_1a.ii:
Write down the value of b.
-
18M.2.SL.TZ2.T_1d:
Find the number of employees who, in the last year, did not travel to work by car, bicycle or public transportation.
-
19M.1.SL.TZ1.T_12c:
Write down the probability that the second spin is yellow, given that the first spin is blue.
-
18N.2.SL.TZ0.T_2a.ii:
Find the number of students in the school that study Mathematics in English.
-
18M.1.SL.TZ2.T_7b:
Find the probability that the boy answered questions in Hindi.
-
18M.2.SL.TZ2.S_9b:
Find the maximum speed of P.
-
19M.1.SL.TZ2.S_10c:
Write down an expression for the area of .
-
17N.2.SL.TZ0.S_5b:
The following diagram shows part of the graph of .
The region enclosed by the graph of , the -axis and the lines and is rotated 360° about the -axis. Find the volume of the solid formed.
-
18M.2.SL.TZ1.T_2g:
Given that this flight was not heavily delayed, find the probability that it travelled between 500 km and 5000 km.
-
17M.1.SL.TZ1.S_10c:
Let , for . The graph of between and is rotated 360° about the -axis. Find the volume of the solid formed.
-
16N.2.SL.TZ0.S_9c:
(i) Find the value of .
(ii) Hence, find the speed of P when .
-
18M.3.AHL.TZ0.Hca_3b:
Illustrate graphically the inequality .
-
19N.1.SL.TZ0.S_8b:
Find an expression for in terms of .
-
18M.1.SL.TZ1.S_5a:
Find .
-
17N.2.SL.TZ0.T_4d:
Find the probability that this adult is allergic to nuts and the liquid turns blue.
-
17N.2.SL.TZ0.S_5a:
Find the value of .
-
22M.1.SL.TZ1.2b:
Hence, find the value of .
-
18M.1.SL.TZ1.S_5b:
Part of the graph of f is shown in the following diagram.
The shaded region R is enclosed by the graph of f, the x-axis, and the lines x = 1 and x = 9 . Find the volume of the solid formed when R is revolved 360° about the x-axis.
-
19M.2.SL.TZ2.S_8e.i:
Given that particles A and B start at the same point, find the displacement function for particle B.
-
22M.1.AHL.TZ1.12b:
Hence, find an approximate value for .
-
20N.1.AHL.TZ0.H_12b:
State the equation of the horizontal asymptote on the graph of .
-
20N.1.AHL.TZ0.H_12d:
Sketch the graph of , stating clearly the equations of any asymptotes and the coordinates of any points of intersections with the coordinate axes.
-
20N.2.AHL.TZ0.H_3b:
Hence find the area of the shaded region.
-
17N.2.SL.TZ0.S_9a:
Write down the values of when .
-
18M.3.AHL.TZ0.Hca_3a:
Find the value of .
-
19M.1.AHL.TZ1.H_8b:
find the value of .
-
18M.2.SL.TZ2.S_3a:
Find the x-intercept of the graph of .
-
16N.2.SL.TZ0.S_4b:
Hence, find the area of the region enclosed by the graphs of and .
-
17N.1.SL.TZ0.S_8d:
Find the area of the region enclosed by the graph of and the line .
-
21M.2.SL.TZ1.9d.i:
Find the -coordinate of the point where intersects the line .
-
21M.2.SL.TZ1.9d.ii:
Hence, find the area of .
-
19M.1.SL.TZ2.S_10d:
Hence find the exact area of .
-
19M.2.SL.TZ2.S_8a:
Find the initial displacement of particle A from point P.
-
19M.2.SL.TZ2.S_8e.ii:
Find the other value of when particles A and B meet.
-
16N.2.SL.TZ0.S_6a:
Use the model to find the volume of the barrel.
-
20N.2.AHL.TZ0.H_3a:
Determine the values of , and .
-
19N.2.AHL.TZ0.H_11c:
The region is now rotated about the -axis, through radians, to form a solid.
By writing as , show that the volume of the solid formed is .
-
18M.2.SL.TZ2.S_3b:
The region enclosed by the graph of , the y-axis and the x-axis is rotated 360° about the x-axis.
Find the volume of the solid formed.
-
19M.2.SL.TZ2.S_2b:
The region enclosed by the graph of , the -axis and the -axis is rotated 360º about the -axis. Find the volume of the solid formed.
-
18M.2.SL.TZ2.S_9c:
Write down the number of times that the acceleration of P is 0 m s−2 .
-
19N.1.SL.TZ0.S_8e:
Find the maximum volume.
-
19N.1.SL.TZ0.S_8d.ii:
Justify your answer.
-
17N.2.SL.TZ0.S_9d:
Find the total distance travelled by P when its velocity is increasing.
-
19N.1.SL.TZ0.S_8c:
Find .
-
19M.1.AHL.TZ1.H_8c:
find the value of .
-
SPM.2.AHL.TZ0.11c:
Sketch the graph of versus for 0 ≤ ≤ 60 and hence find the maximum amount of salt in the tank and the value of at which this occurs.
-
19M.2.SL.TZ2.S_2a:
Find the -intercept of the graph of .
-
21M.2.SL.TZ1.1a:
Find .
-
17M.2.SL.TZ1.S_10a.i:
Write down the value of ;
-
22M.2.SL.TZ2.2:
The derivative of a function is given by , where . The graph of passes through the point . Find .
-
21N.1.SL.TZ0.7c:
Find the total distance travelled by .
-
21N.1.SL.TZ0.7a.ii:
Show that the distance of from at this time is metres.
-
22M.1.AHL.TZ1.1:
Find the value of .
-
18M.1.SL.TZ2.T_7a:
State the number of boys who answered questions in Portuguese.
-
17N.1.SL.TZ0.T_7b:
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.
-
16N.2.SL.TZ0.T_2d:
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.
-
19M.1.SL.TZ2.T_5c:
A student is chosen at random from the surveyed students.
Find the probability that this student likes kiwi fruit smoothies given that they like mango smoothies.
-
18M.2.SL.TZ1.T_2e:
State, with a reason, whether you would reject the null hypothesis.
-
17N.1.SL.TZ0.T_7c:
Determine whether the events and are independent.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
SPM.2.AHL.TZ0.11b:
Hence, by solving this differential equation, show that .
-
19M.2.SL.TZ2.S_8b:
Find the value of when particle A first reaches point P.
-
17N.2.SL.TZ0.S_9c:
Find an expression for the velocity of P at time .
-
18M.2.SL.TZ1.T_2h:
Two flights are chosen at random from those which were slightly delayed.
Find the probability that each of these flights travelled at least 5000 km.
-
SPM.2.AHL.TZ0.11e:
The rate of change of the amount of salt leaving the tank is equal to .
Find the amount of salt that left the tank during the first 60 minutes.
-
18M.2.SL.TZ1.S_4c:
Find the area of the region enclosed by the graphs of f and g.
-
17M.2.SL.TZ2.S_7:
Note: In this question, distance is in metres and time is in seconds.
A particle moves along a horizontal line starting at a fixed point A. The velocity of the particle, at time , is given by , for . The following diagram shows the graph of

There are -intercepts at and .
Find the maximum distance of the particle from A during the time and justify your answer.
-
17M.1.SL.TZ1.S_10a:
Show that .
-
20N.1.AHL.TZ0.H_12a:
State the equation of the vertical asymptote on the graph of .
-
20N.1.AHL.TZ0.H_12c:
Use an algebraic method to determine whether is a self-inverse function.
-
19N.1.AHL.TZ0.H_10c:
Show that .
-
19M.1.SL.TZ2.S_10b:
Hence find .
-
20N.1.AHL.TZ0.H_12e:
The region bounded by the -axis, the curve , and the lines and is rotated through about the -axis. Find the volume of the solid generated, giving your answer in the form , where .
-
17M.2.SL.TZ1.S_7b:
A second particle Q also moves along a straight line. Its velocity, after seconds is given by for . After seconds Q has travelled the same total distance as P.
Find .
-
16N.2.SL.TZ0.S_4a:
Find the value of and of .
-
19N.2.AHL.TZ0.H_11b:
Find the area of .
-
18N.2.SL.TZ0.T_2c.iii:
Find the probability that this student is taught in Spanish, given that the student studies Biology.
-
19N.1.AHL.TZ0.H_10d:
The area enclosed by the graph of and the line can be expressed as . Find the value of .
-
18M.3.AHL.TZ0.Hca_3d:
Find an upper bound for .
-
19M.1.SL.TZ1.S_7a:
Find the value of .
-
18M.2.SL.TZ1.T_2b:
Calculate the expected frequency of flights travelling at most 500 km and arriving slightly delayed.
-
16N.2.SL.TZ0.S_9d:
(i) Find the total distance travelled by P between and .
(ii) Hence or otherwise, find the displacement of P from A when .
-
21M.2.SL.TZ1.1b:
Given and , find .
-
17M.2.SL.TZ1.S_10a.iii:
Write down the value of .
-
17M.2.SL.TZ1.S_10c:
Let be the vertical distance from a point on the graph of to the line . There is a point on the graph of where is a maximum.
Find the coordinates of P, where .
-
17M.2.SL.TZ1.S_10a.ii:
Write down the value of ;
-
17M.2.SL.TZ1.S_10b.ii:
Hence, find the area of the region enclosed by the graphs of and .
-
18N.2.SL.TZ0.T_2a.i:
Find the number of students in the school that are taught in Spanish.
-
18N.2.SL.TZ0.T_2a.iii:
Find the number of students in the school that study both Biology and Mathematics.
-
19M.2.SL.TZ2.T_1d:
State whether or not H0 should be rejected. Justify your statement.
-
17N.2.SL.TZ0.T_4c:
Copy and complete the tree diagram.
-
18M.2.SL.TZ1.T_2c:
Write down the number of degrees of freedom.
-
19M.1.SL.TZ2.T_5b:
Find the number of surveyed students who did not like any of the three flavours.
-
18M.2.SL.TZ1.T_5d.ii:
A contestant is chosen at random. Find the probability that this contestant fell into a trap.
-
18N.2.SL.TZ0.T_2c.i:
Find the probability that this student studies Mathematics.
-
19M.2.SL.TZ2.T_1e.i:
Find the probability that the student does not take the Spanish class.
-
16N.2.SL.TZ0.T_2b:
Show that .
-
18M.2.SL.TZ1.T_5d.i:
A contestant is chosen at random. Find the probability that this contestant fell into a trap while attempting to pass through a door in the second wall.
-
18M.1.SL.TZ2.T_7c:
Two girls are selected at random.
Calculate the probability that one girl answered questions in Mandarin and the other answered questions in Hindi.
-
19M.1.SL.TZ1.T_12b:
Find the probability that at least one of the spins is yellow.
-
17N.2.SL.TZ0.T_4e:
Find the probability that the liquid turns blue.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
21N.1.SL.TZ0.7a.i:
Find the value of when reaches its maximum velocity.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
18M.2.SL.TZ1.T_2f:
Write down the probability that this flight arrived on time.
-
19M.2.SL.TZ2.T_1e.ii:
Find the probability that neither of the two students take the Spanish class.
-
18M.2.SL.TZ2.T_1a.i:
Write down the value of a.
-
18M.2.SL.TZ2.T_1b.i:
Use the tree diagram to find the probability that an employee encountered traffic and was late for work.
-
18M.2.SL.TZ2.T_1b.ii:
Use the tree diagram to find the probability that an employee was late for work.
-
18M.2.SL.TZ2.T_1b.iii:
Use the tree diagram to find the probability that an employee encountered traffic given that they were late for work.
-
18M.2.SL.TZ2.T_1e:
Find .
-
16N.2.SL.TZ0.T_2a:
Draw a Venn diagram to represent the given information, using sets labelled , and .
-
16N.2.SL.TZ0.T_2c:
Write down the value of .
-
18N.2.SL.TZ0.T_2c.ii:
Find the probability that this student studies neither Biology nor Mathematics.
-
17N.2.SL.TZ0.T_4b:
Find the probability that both people chosen are not allergic to nuts.
-
17N.2.SL.TZ0.T_4f:
Find the probability that the tested adult is allergic to nuts given that the liquid turned blue.
-
18M.2.SL.TZ1.T_5b:
Find the probability that only one of Ayako and Natsuko falls into a trap while attempting to pass through a door in the first wall.
-
19M.2.SL.TZ2.T_1b:
State the number of degrees of freedom.

