| Date | November 2018 | Marks available | 1 | Reference code | 18N.2.SL.TZ0.T_2 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Write down | Question number | T_2 | Adapted from | N/A |
Question
160 students attend a dual language school in which the students are taught only in Spanish or taught only in English.
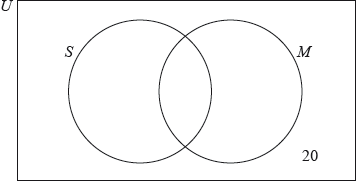
A survey was conducted in order to analyse the number of students studying Biology or Mathematics. The results are shown in the Venn diagram.
Set S represents those students who are taught in Spanish.
Set B represents those students who study Biology.
Set M represents those students who study Mathematics.
A student from the school is chosen at random.
Find the number of students in the school that are taught in Spanish.
Find the number of students in the school that study Mathematics in English.
Find the number of students in the school that study both Biology and Mathematics.
Write down .
Write down .
Find the probability that this student studies Mathematics.
Find the probability that this student studies neither Biology nor Mathematics.
Find the probability that this student is taught in Spanish, given that the student studies Biology.
Markscheme
10 + 40 + 28 + 17 (M1)
= 95 (A1)(G2)
Note: Award (M1) for each correct sum (for example: 10 + 40 + 28 + 17) seen.
[2 marks]
20 + 12 (M1)
= 32 (A1)(G2)
Note: Award (M1) for each correct sum (for example: 10 + 40 + 28 + 17) seen.
[2 marks]
12 + 40 (M1)
= 52 (A1)(G2)
Note: Award (M1) for each correct sum (for example: 10 + 40 + 28 + 17) seen.
[2 marks]
78 (A1)
[1 mark]
12 (A1)
[1 mark]
(A1)(A1) (G2)
Note: Throughout part (c), award (A1) for correct numerator, (A1) for correct denominator. All answers must be probabilities to award (A1).
[2 marks]
(A1)(A1) (G2)
Note: Throughout part (c), award (A1) for correct numerator, (A1) for correct denominator. All answers must be probabilities to award (A1).
[2 marks]
(A1)(A1) (G2)
Note: Throughout part (c), award (A1) for correct numerator, (A1) for correct denominator. All answers must be probabilities to award (A1).
[2 marks]