DP Mathematics: Analysis and Approaches Questionbank

SL 4.5—Probability concepts, expected numbers
Description
[N/A]Directly related questions
-
20N.1.SL.TZ0.S_8a:
Find the value of .
-
20N.1.SL.TZ0.S_8b:
Write down the value of the median distance in kilometres (km).
-
20N.1.SL.TZ0.S_8c:
Find the value of .
-
20N.1.SL.TZ0.S_8d:
Find .
-
20N.1.SL.TZ0.S_8e:
The first athletes that completed the race won a prize.
Given that an athlete took between and minutes to complete the race, calculate the probability that they won a prize.
-
20N.2.SL.TZ0.S_9a:
Find the probability that it will take Fiona between minutes and minutes to walk to the bus stop.
-
20N.2.SL.TZ0.S_9b:
Find .
-
20N.2.SL.TZ0.S_9c:
Find the probability that the bus journey takes less than minutes.
-
20N.2.SL.TZ0.S_9d:
Find the probability that Fiona will arrive on time.
-
20N.2.SL.TZ0.S_9e:
This year, Fiona will go to school on days.
Calculate the number of days Fiona is expected to arrive on time.
-
20N.1.SL.TZ0.T_6a.i:
Find the probability that the first ball chosen is labelled .
-
20N.1.SL.TZ0.T_6a.ii:
Find the probability that the first ball chosen is labelled or labelled .
-
20N.1.SL.TZ0.T_6b:
Find the probability that the second ball chosen is labelled , given that the first ball chosen was labelled .
-
20N.1.SL.TZ0.T_6c:
Find the probability that both balls chosen are labelled .
-
22M.1.SL.TZ2.9c:
Assuming that rolls of the die are independent, find the probability that Nicky wins the game.
-
19M.2.SL.TZ1.S_10a.i:
Find the probability of rolling exactly one red face.
-
19M.2.SL.TZ1.S_10a.ii:
Find the probability of rolling two or more red faces.
-
19M.2.SL.TZ1.S_10b:
Show that, after a turn, the probability that Ted adds exactly $10 to his winnings is .
-
19M.2.SL.TZ1.S_10c.i:
Write down the value of .
-
19M.2.SL.TZ1.S_10c.ii:
Hence, find the value of .
-
19M.2.SL.TZ1.S_10d:
Ted will always have another turn if he expects an increase to his winnings.
Find the least value of for which Ted should end the game instead of having another turn.
-
17M.1.SL.TZ1.S_1a.i:
Find the value of ;
-
17M.1.SL.TZ1.S_1a.ii:
Find the value of .
-
17M.1.SL.TZ1.S_1b:
A girl is selected at random. Find the probability that she takes economics but not history.
-
18N.1.SL.TZ0.S_9a.i:
Find the probability, in terms of , that the game will end on her first draw.
-
18N.1.SL.TZ0.S_9a.ii:
Find the probability, in terms of , that the game will end on her second draw.
-
18N.1.SL.TZ0.S_9b.i:
third draw.
-
18N.1.SL.TZ0.S_9b.ii:
fourth draw.
-
18N.1.SL.TZ0.S_9c:
Hayley plays the game when = 5. She pays $20 to play and can earn money back depending on the number of draws it takes to obtain a blue marble. She earns no money back if she obtains a blue marble on her first draw. Let M be the amount of money that she earns back playing the game. This information is shown in the following table.
Find the value of so that this is a fair game.
-
18N.2.SL.TZ0.S_1a:
Write down the number of students in the group who take art class.
-
18N.2.SL.TZ0.S_1b.i:
the student does not take art class.
-
18N.2.SL.TZ0.S_1b.ii:
the student takes either art class or music class, but not both.
-
17N.1.SL.TZ0.T_7a:
Complete the Venn diagram for these students.
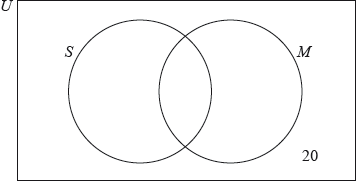
-
17N.1.SL.TZ0.T_7b:
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.
-
17N.1.SL.TZ0.T_7c:
Determine whether the events and are independent.
-
16N.2.SL.TZ0.T_2a:
Draw a Venn diagram to represent the given information, using sets labelled , and .
-
16N.2.SL.TZ0.T_2b:
Show that .
-
16N.2.SL.TZ0.T_2c:
Write down the value of .
-
16N.2.SL.TZ0.T_2d:
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.
-
18N.2.SL.TZ0.T_2a.i:
Find the number of students in the school that are taught in Spanish.
-
18N.2.SL.TZ0.T_2a.ii:
Find the number of students in the school that study Mathematics in English.
-
18N.2.SL.TZ0.T_2a.iii:
Find the number of students in the school that study both Biology and Mathematics.
-
18N.2.SL.TZ0.T_2b.i:
Write down .
-
18N.2.SL.TZ0.T_2b.ii:
Write down .
-
18N.2.SL.TZ0.T_2c.i:
Find the probability that this student studies Mathematics.
-
18N.2.SL.TZ0.T_2c.ii:
Find the probability that this student studies neither Biology nor Mathematics.
-
18N.2.SL.TZ0.T_2c.iii:
Find the probability that this student is taught in Spanish, given that the student studies Biology.
-
19M.1.SL.TZ2.T_5a:
Using the given information, complete the following Venn diagram.
-
19M.1.SL.TZ2.T_5b:
Find the number of surveyed students who did not like any of the three flavours.
-
19M.1.SL.TZ2.T_5c:
A student is chosen at random from the surveyed students.
Find the probability that this student likes kiwi fruit smoothies given that they like mango smoothies.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
