19.1.1 Electrochemical Cells

• We have seen previously that redox reactions involve simultaneous oxidation and reduction as electrons flow from the reducing agent to the oxidizing agent
• Which way electrons flow depends on the reactivity of the species involved
• Redox chemistry has very important applications in electrochemical cells, which come in two types:
  • Voltaic cells
  • Electrolytic cells

Voltaic cells

• A voltaic cell generates a potential difference known as an electromotive force or EMF
• The EMF is also called the cell potential and given the symbol E
• The absolute value of a cell potential cannot be determined only the difference between one cell and another
  • This is analogous to arm-wrestling: you cannot determine the strength of an arm-wrestler unless you compare her to the other competitors
• Voltaic (or Galvanic) cells generate electricity from spontaneous redox reactions
• For example:

Zn (s)  + CuSO₄ (aq)→ Cu (s)  + ZnSO₄ (aq)

• Instead of electrons being transferred directly from the zinc to the copper ions, a cell is built which separates the two redox processes
• Each part of the cell is called a half cell
• If a rod of metal is dipped into a solution of its own ions, an equilibrium is set up
• For example:

Zn (s)  ⇌  Zn²⁺ (aq) + 2e^– 

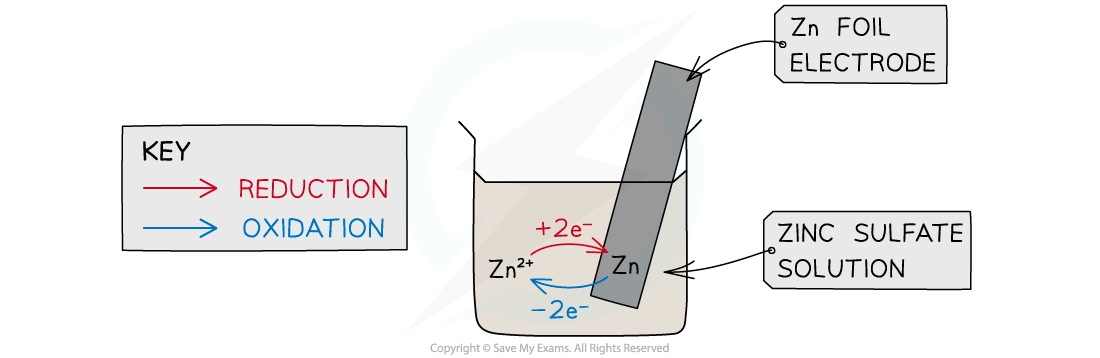
When a metal is dipped into a solution contains its ions an equilibrium is established between the metal and it ions

Creating an EMF

• If two different electrodes are connected, the potential difference between the two electrodes will cause a current to flow between them. Thus an electromotive force (EMF) is established and the system can generate electrical energy
• A typical electrochemical cell can be made by combining a zinc electrode in a solution of zinc sulfate with a copper electrode in a solution of copper sulfate

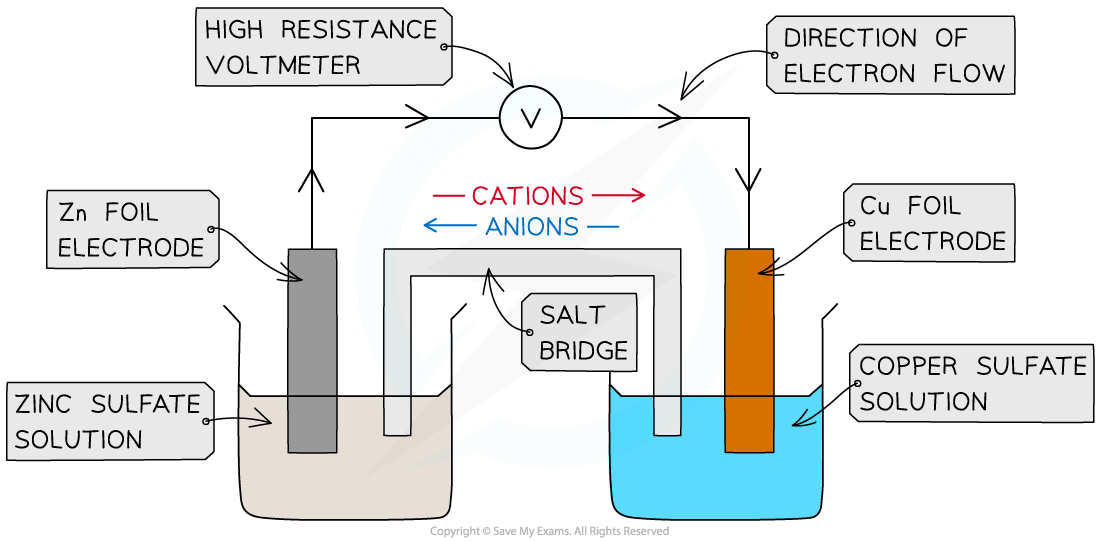
The zinc-copper voltaic cell (also known as the Daniell Cell)

• The circuit must be completed by allowing ions to flow from one solution to the other
• This is achieved by means of a salt bridge
  • This is often a piece of filter paper saturated with a solution of an inert electrolyte such as KNO₃(aq)
• The EMF can be measured using a voltmeter
  • Voltmeters have a high resistance so that they do not divert much current from the main circuit

• The two half cells are said to be in series as the same current is flowing through both cells
• The combination of two electrodes in this way is known as a voltaic cell, and can be used to generate electricity

• Voltmeters measure potential on the right-hand side of the cell and subtract it from the potential on the left-hand side of the cell

EMF= E_right - E_left

• Sometimes this can be hard to remember, but it helps if you remember the phrase 'knives & forks'

You hold your knife in your right hand and your fork in your left hand. EMF is right minus left

• If the standard hydrogen electrode is placed on the left-hand side of the voltmeter, then by convention E_left will be zero and the EMF of the cell will be the electrode potential of the right-hand electrode
• For example, if the standard zinc electrode is connected to the standard hydrogen electrode and the standard hydrogen electrode is placed on the left, the voltmeter measures -0.76V.

Zn²⁺(aq) + 2e^- ⇌ Zn(s)

• • The   Zn²⁺(aq) + 2e^- ⇌ Zn(s) half-cell thus has an electrode potential of -0.76V

• If the Cu²⁺(aq) + 2e^- ⇌ Cu(s) electrode is connected to the standard hydrogen electrode and the standard hydrogen electrode is placed on the left, the voltmeter reads +0.34V
  • The Cu²⁺(aq) + 2e^- ⇌ Cu(s) half-cell thus has an electrode potential of +0.34V.

Standard electrode potential

• The standard electrode potential of a half-reaction is the emf of a cell where the left-hand electrode is the standard hydrogen electrode and the right-hand electrode is the standard electrode in question
• The equation EMF = E_RHS - E_LHS  can be applied to electrochemical cells in two ways:
  • Calculating an unknown standard electrode potential
  • Calculating a cell EMF

• To be a standard electrode potential the measurements must be made at standard conditions, namely:
  • 1.0 mol dm^-3 ions concentrations
  • 100 kPa pressure
  • 298 K

Calculating an unknown standard electrode potential

• If the RHS and LHS electrode are specified, and the EMF of the cell measured accordingly, then if the E^θ of one electrode is known then the other can be deduced.
  • For example, if the standard copper electrode (+0.34 V) is placed on the left, and the standard silver electrode is placed on the right, the EMF of the cell is +0.46 V.
  • Calculate the standard electrode potential at the silver electrode.

EMF = E_RHS - E_LHS

+0.46 = E^θ_Ag - (+0.34 V)

E^θ_Ag = 0.46 + 0.34 = +0.80 V

Calculating a cell EMF

• If both SEP's are known, the EMF of the cell formed can be calculated if the right-hand electrode and left-hand electrode are specified
  • For example, if in a cell the RHS = silver electrode (+0.80V) and LHS is copper electrode (+0.34 V), then

EMF = E_RHS - E_LHS

EMF = +0.80 - 0.34 = +0.46 V

Conventional Representation of Cells

• As it is cumbersome and time-consuming to draw out every electrochemical cell in full, a system of notation is used which describes the cell in full, but does not require it to be drawn.
• An electrochemical cell can be represented in a shorthand way by a cell diagram (sometimes called cell representations or cell notations)

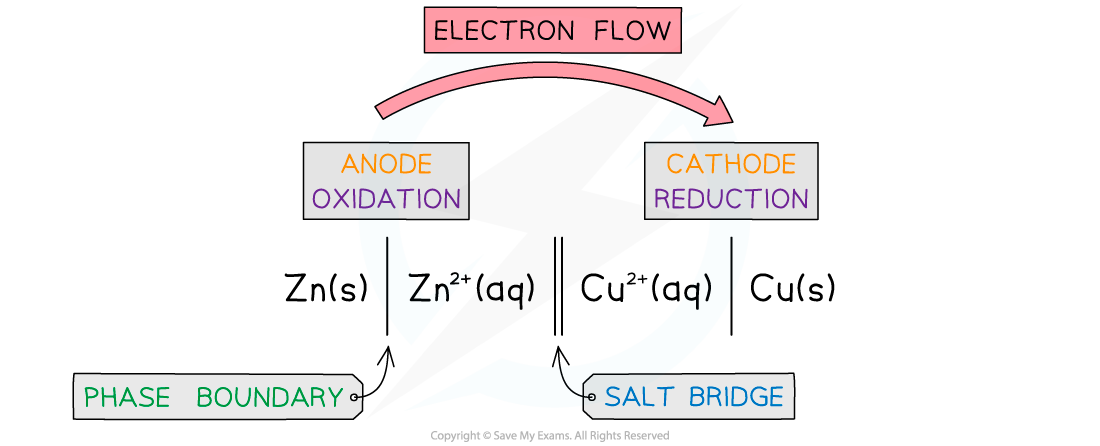
The conventional representation of voltaic cells

• By convention, the half cell with the greatest negative potential is written on the left of the salt bridge, so E^θ_cell = E^θ_right – E^θ_left
  • In this case, E^θ_cell = +0.34 – -0.76 = +1.10 V.

• The left cell is being oxidized while the right is being reduced
• If there is more than one species in solution, and the species are on different sides of the half-equation, the different species are separated by a comma
• This method of representing electrochemical cells is known as the conventional representation of a cell, and it is widely used
• If both species in a half reaction are aqueous then an inert platinum electrode is needed which is recorded on the outside of the half cell diagram

Some Examples

• For the iron(II) and iron(III) half cell reaction a platinum electrode is needed as an electron carrier
• The half equation is

Fe³⁺(aq) + e^- ⇌ Fe²⁺(aq)

• So the cell convention as a left hand electrode would be

Pt 丨Fe²⁺(aq), Fe³⁺(aq)

• Notice the order must be Fe(II) then Fe(III) as the left side is an oxidation reaction, so Fe(II) is oxidised to Fe(III) by the loss of an electron
• The platinum electrode is separated by the phase boundary (vertical solid line), but the iron(II) and iron(III) are separated by a comma since they are in the same phase
• Non-metals will also require a platinum electrode
• If chlorine is used as an electrode the reduction reaction is

Cl₂(g) + 2e^- ⇌ 2Cl^-(aq)

• The conventional representation of the half reaction would be

Cl₂ (g), 2Cl^- (aq) | Pt 

• Notice that the half cell reaction is balanced; however, it would be also correct to write it as

Cl₂ (g), Cl^- (aq) | Pt 

• This is because conventional cell diagrams are not quantitative- they are just representations of the materials and redox processes going on
  • Most chemists tend to show them balanced anyway

• Combining these two half cells together gives

Pt  | Fe²⁺(aq), Fe³⁺(aq)  ∥  Cl₂ (g), 2Cl^- (aq) | Pt

• As you can see the overall cell diagram is not quantitative as the left side is a one electron transfer and the right side is a two electron transfer