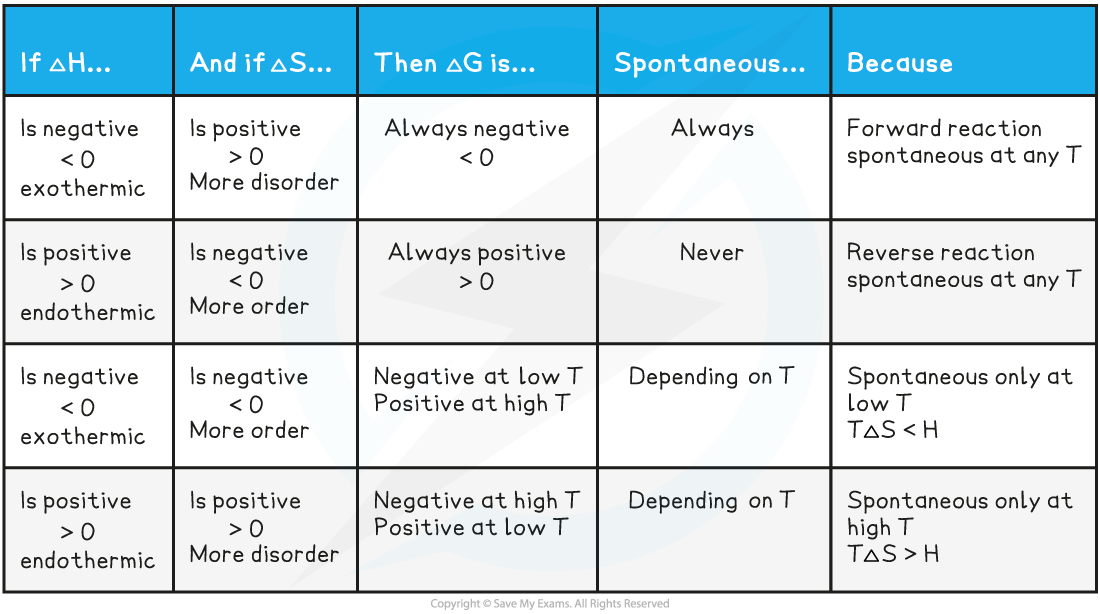
Spontaneous Reactions
- Gibbs free energy provides an effective way of focusing on a reaction system at constant temperature and pressure to determine its spontaneity
- For a reaction to be spontaneous, Gibbs free energy must be have a negative value (ΔGꝋ ≤ 0)
- We can use the Gibbs equation to calculate whether a reaction is spontaneous / feasible or not
ΔGꝋ = ΔHreactionꝋ – TΔSsystemꝋ
-
- When ΔGꝋ is negative, the reaction is spontaneous / feasible and likely to occur
- When ΔGꝋ is positive, the reaction is not spontaneous / feasible and unlikely to occur
- We can also look at the the values for enthalpy change, ΔH, and entropy change, ΔS
- Depending on the value for ΔH and ΔS we can determine whether the reaction is spontaneous at a given temperature (T)
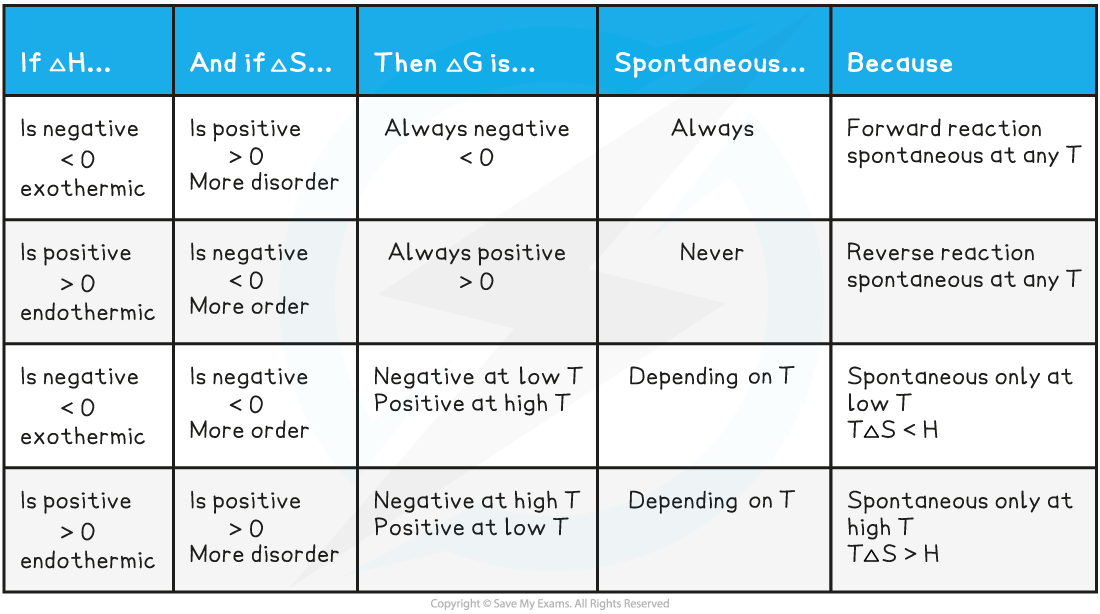
Factors affecting ΔG and the spontaneity / feasibility of a reaction
Worked Example
Determining if a reaction is feasible / spontaneous
- Calculate the Gibbs free energy change for the following reaction at 298 K
- Determine whether the reaction is feasible.
2Ca (s) + O2 (g) → 2CaO (s) ΔH = -635.5 kJ mol-1
- Sꝋ[Ca(s)] = 41.00 J K-1 mol-1
- Sꝋ[O2(g)] = 205.0 J K-1 mol-1
- Sꝋ[CaO(s)] = 40.00 J K-1 mol-1
Answers:
Answer 1:
Step1: Calculate ΔSsystemꝋ
- ΔSsystemꝋ = ΣΔSproductsꝋ – ΣΔSreactantsꝋ
ΔSsystemꝋ = (2 x ΔSꝋ [CaO(s)]) – (2 x ΔSꝋ [Ca(s)] + ΔSꝋ [O2(g)])
= (2 x 40.00) – (2 x 41.00 + 205.0)
= -207.0 J K-1 mol-1
Step 2:Convert ΔSꝋ to kJ K-1 mol-1
- ΔSsystemꝋ = -207.0 J K-1 mol-1 ÷ 1000 = -0.207 kJ mol-1
Step 3: Calculate ΔGꝋ
- ΔGꝋ = ΔHreactionꝋ – TΔSsystemꝋ
ΔGꝋ = -635.5 – (298 x -0.207)
= –573.8 kJ mol-1
Answer 2:
- Since ΔGꝋ is negative, the reaction is feasible
Factors affecting ΔG and the spontaneity / feasibility of a reaction
- We can also look at the the values for ΔH and ΔS to determine whether the reaction is spontaneous / feasible at a given temperature (T)
- The Gibbs equation will be used to explain what will affect the spontaneity / feasibility of a reaction for exothermic and endothermic reactions

Exothermic reactions
- In exothermic reactions, ΔHreactionꝋ is negative
- If the ΔSsystemꝋ is positive:
- Both the first and second term will be negative
- Resulting in a negative ΔGꝋ so the reaction is feasible
- Therefore, regardless of the temperature, an exothermic reaction with a positive ΔSsystemꝋ will always be feasible
- If the ΔSsystemꝋ is negative:
- The first term is negative and the second term is positive
- At very high temperatures, the –TΔSsystemꝋ will be very large and positive and will overcome ΔHreactionꝋ
- Therefore, at high temperatures ΔGꝋ is positive and the reaction is not feasible
- Since the relative size of an entropy change is much smaller than an enthalpy change, it is unlikely that TΔS > ΔH as temperature increases
- These reactions are therefore usually spontaneous at normal conditions
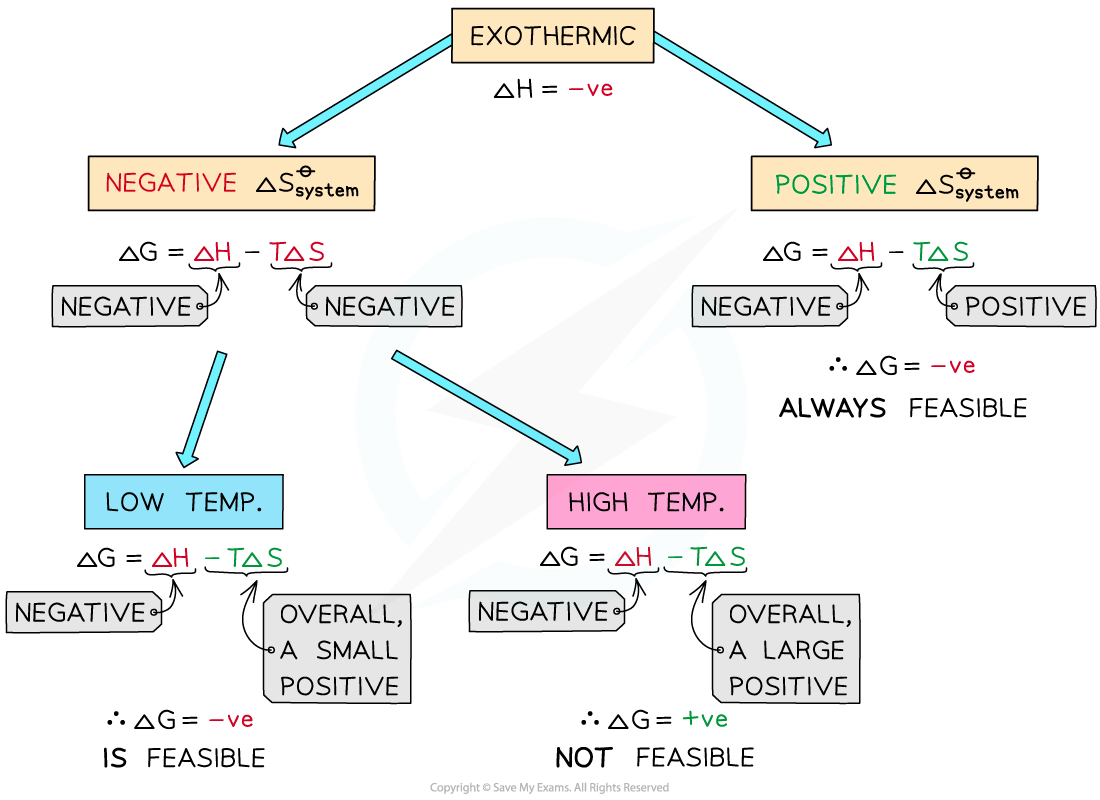
The diagram shows under which conditions exothermic reactions are feasible
Endothermic reactions
- In endothermic reactions, ΔHreactionꝋ is positive
- If the ΔSsystemꝋ is negative:
- Both the first and second term will be positive
- Resulting in a positive ΔGꝋ so the reaction is not feasible
- Therefore, regardless of the temperature, endothermic with a negative ΔSsystemꝋ will never be feasible
- If the ΔSsystemꝋ is positive:
- The first term is positive and the second term is negative
- At low temperatures, the –TΔSsystemꝋ will be small and negative and will not overcome the larger ΔHreactionꝋ
- Therefore, at low temperatures ΔGꝋ is positive and the reaction is not feasible
- The reaction is more feasible at high temperatures as the second term will become negative enough to overcome the ΔHreactionꝋ resulting in a negative ΔGꝋ
- This tells us that for certain reactions which are not feasible at room temperature, they can become feasible at higher temperatures
- An example of this is found in metal extractions, such as the extraction if iron in the blast furnace, which will be unsuccessful at low temperatures but can occur at higher temperatures (~1500 oC in the case of iron)
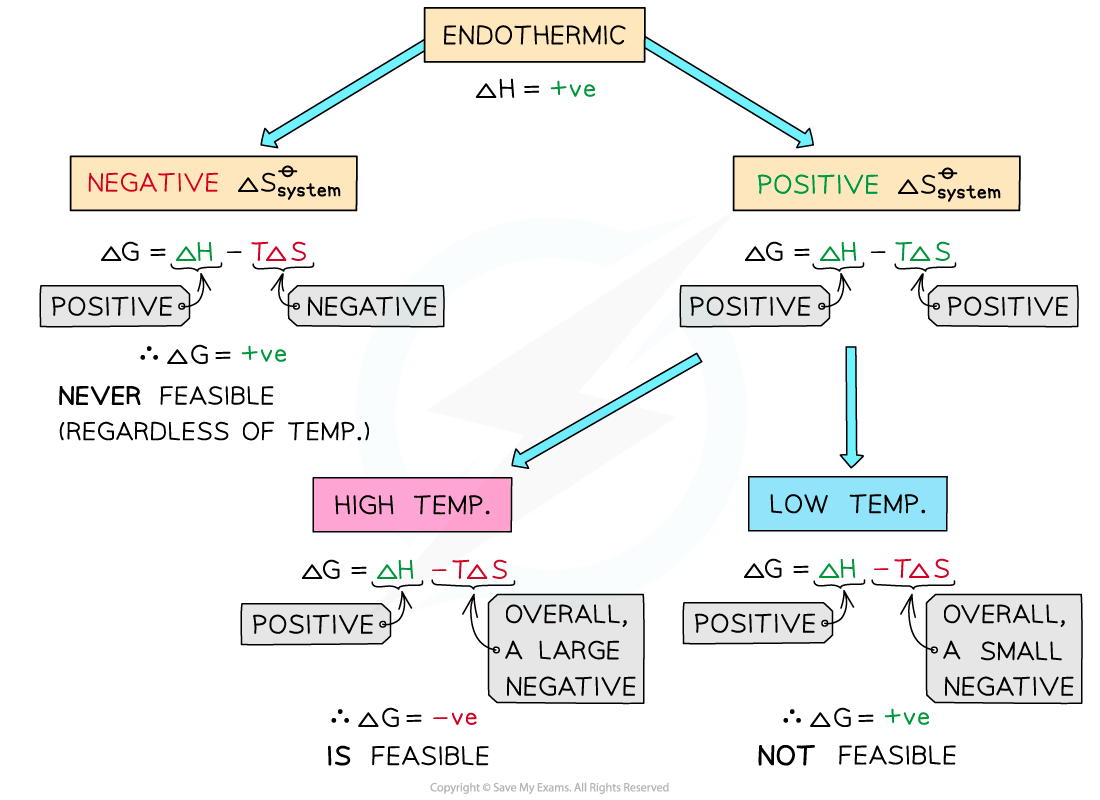
The diagram shows under which conditions endothermic reactions are feasible
Summary of factors affecting Gibbs free energy