Born-Haber Cycle Calculations
- Once a Born-Haber cycle has been constructed, it is possible to calculate the lattice energy (ΔHlatꝋ) by applying Hess’s law and rearranging:
ΔHfꝋ = ΔHatꝋ + ΔHatꝋ + IE + EA + ΔHlatꝋ
- If we simplify this into three terms, this makes the equation easier to see:
- ΔHlatꝋ
- ΔHfꝋ
- ΔH1ꝋ (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)
- The simplified equation becomes:
ΔHfꝋ = ΔH1ꝋ + ΔHlatꝋ
- So, if we rearrange to calculate the lattice energy, the equation becomes
ΔHlatꝋ = ΔHfꝋ - ΔH1ꝋ
- When calculating the ΔHlatꝋ, all other necessary values will be given in the question
- A Born-Haber cycle could be used to calculate any stage in the cycle
- For example, you could be given the lattice energy and asked to calculate the enthalpy change of formation of the ionic compound
- The principle would be exactly the same
- Work out the direct and indirect route of the cycle (the stage that you are being asked to calculate will always be the direct route)
- Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value
- Remember: sometimes a value may need to be doubled or halved, depending on the ionic solid involved
- For example, with MgCl2 the value for the first electron affinity of chlorine would need to be doubled in the calculation, because there are two moles of chlorine atoms
- Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of chloride ions, i.e. 2Cl-
Worked Example
Calculating the lattice energy of KClGiven the data below, calculate the ΔHlatꝋ of potassium chloride (KCl) 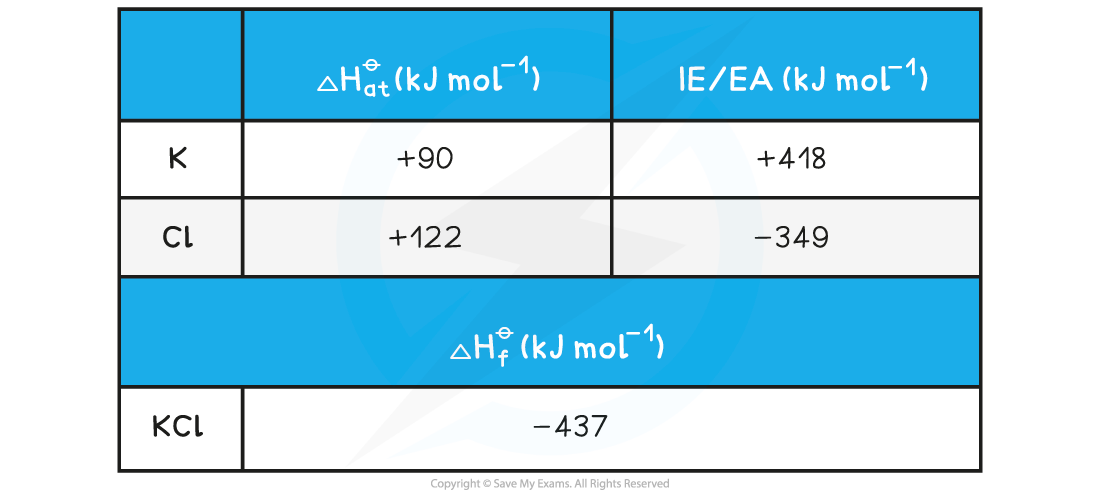
Answer
Step 1: Construct the Born-Haber cycle
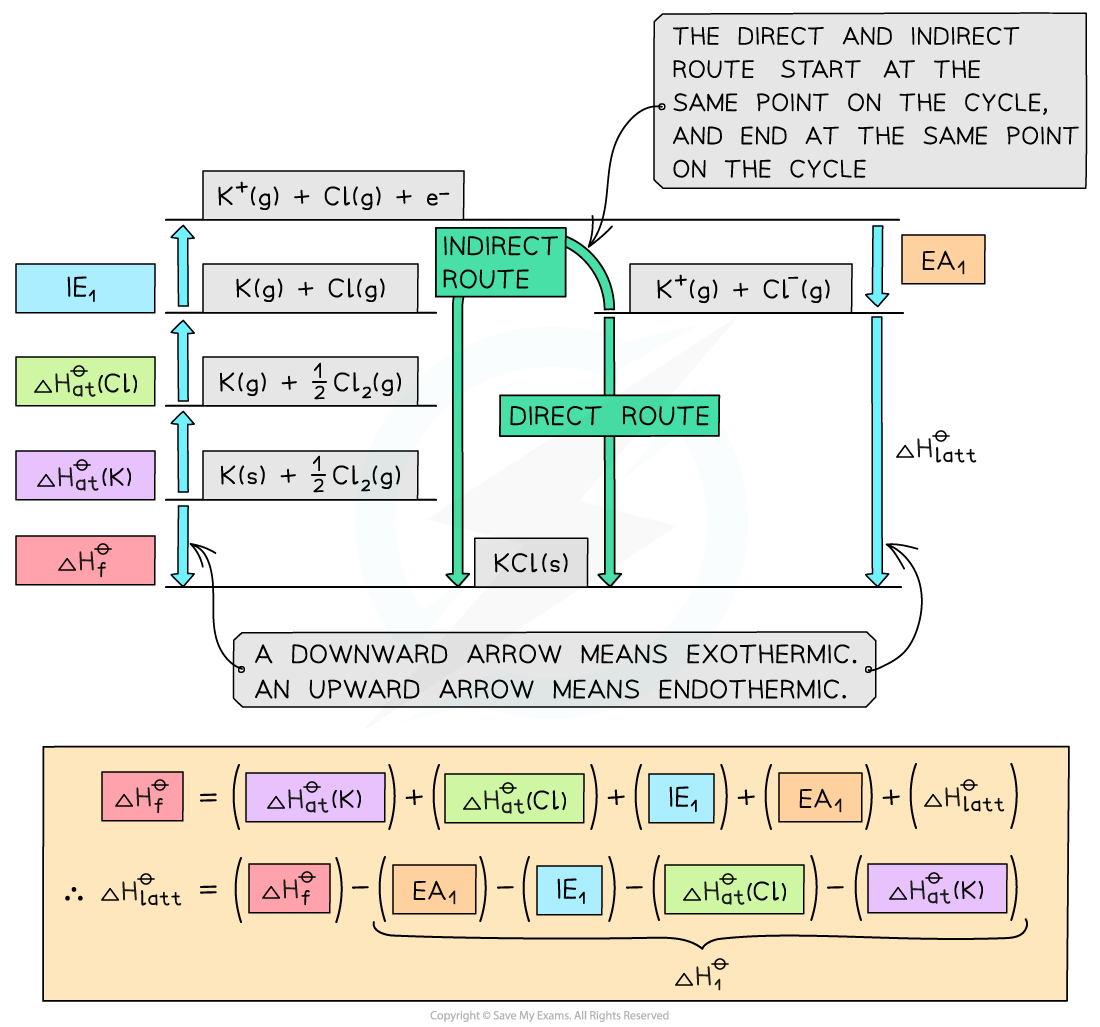
Step 2: Applying Hess’ law, the lattice energy of KCl is:
ΔHlatꝋ = ΔHfꝋ - ΔH1ꝋ
ΔHlattꝋ = ΔHfꝋ - [(ΔHatꝋ K) + (ΔHatꝋ Cl) + (IE1 K) + (EA1 Cl)]
Step 3: Substitute in the numbers:
ΔHlatꝋ = (-437) - [(+90) + (+122) + (+418) + (-349)] = -718 kJ mol-1
Worked Example
Calculating the lattice energy of MgOGiven the data below, calculate the of ΔHlatꝋ magnesium oxide of magnesium oxide (MgO)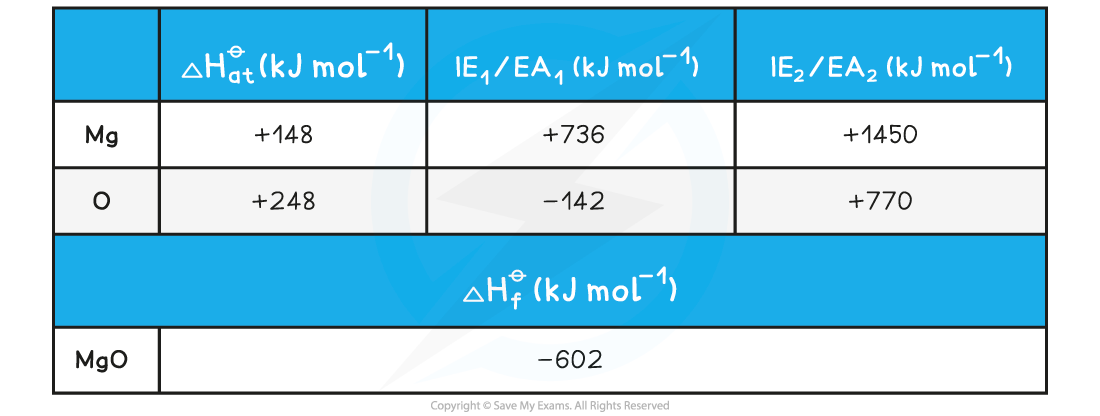
Answer
Step 1: Construct the Born-Haber cycle
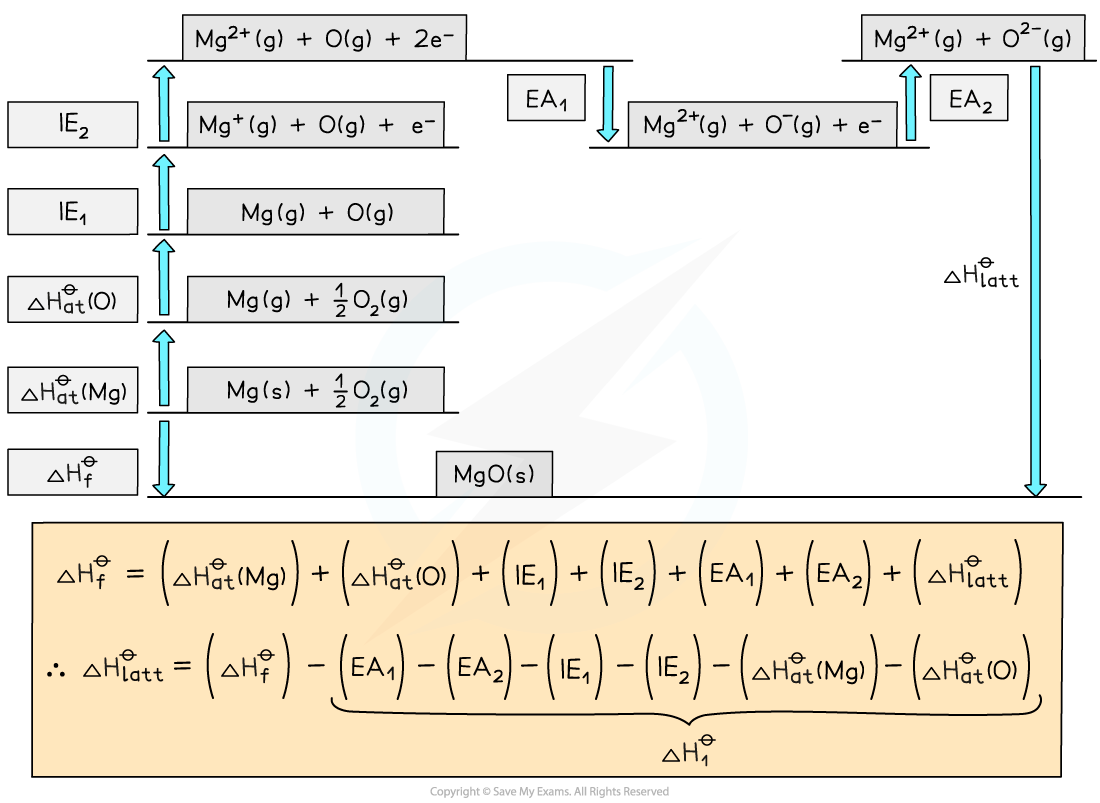
Step 2: Applying Hess’ law, the lattice energy of MgO is:
ΔHlattꝋ = ΔHfꝋ - ΔH1ꝋ
ΔHlatꝋ = ΔHfꝋ - [(ΔHatꝋ Mg) + (ΔHatꝋ O) + (IE1 Mg) + (IE2 Mg) + (EA1 O) + (EA2 O)]
Step 3: Substitute in the numbers:
ΔHlatꝋ = (-602) - [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]
= -3812 kJ mol-1
Size & Charge of Ions & Lattice Enthalpy
Factors affecting lattice enthalpy
- The two key factors which affect lattice energy, ΔHlatꝋ, are the ionic charge and ionic radii of the ions that make up the crystalline lattice
Ionic Radius
- The radius of the anion increases as you move down a group
- As the distance between the bonded ions increases, the strength of the electrostatic attraction decreases
- This is reflected by a decrease in the lattice enthalpy
- The lattice enthalpy becomes more negative or more exothermic as the ionic radius of the ions increases
- This is because the charge on the ions is more spread out over the ion when the ions are larger
- The ions are also further apart from each other in the lattice
- The attraction between ions is between the centres of the ions involved, so the bigger the ions the bigger the distance between the centre of the ions
- Therefore, the electrostatic forces of attraction between the oppositely charged ions in the lattice are weaker
- For example, down group 17, the ionic radii increases which directly influences the lattice enthalpy
Lattice enthalpies of sodium halides
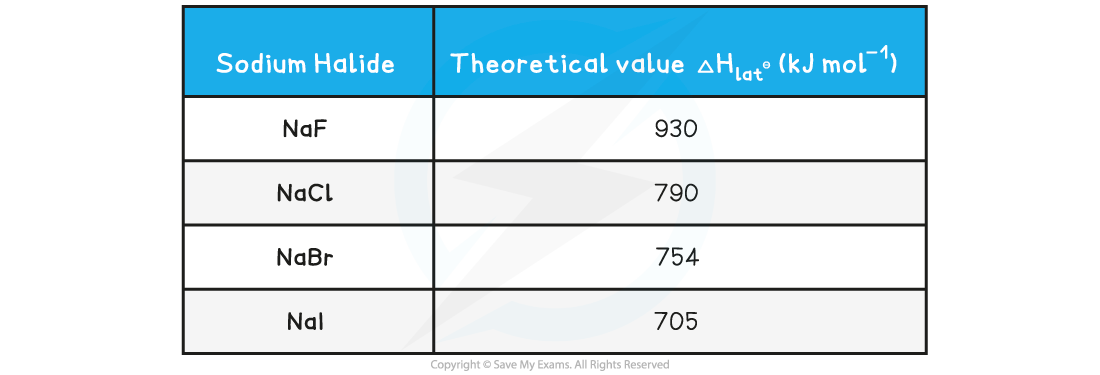
Ionic Charge
- Increasing the ionic charge will result in an increased attraction between oppositely charged ions
- This will increase the energy required to break the lattice apart, and therefore increase the lattice enthalpy (becomes more positive or more endothermic)
- The greater the ionic charge, the higher the charge density
- This results in stronger electrostatic attraction between the oppositely charged ions in the lattice
- As a result, the lattice enthalpy is more endothermic
- For example, the lattice energy of calcium oxide (CaO) is more endothermic than the lattice energy of potassium chloride (KCl)
Lattice enthalpies with varying ionic charges and radii

Exam Tip
The answers for these calculations are given as negative values, which shows they are exothermicWe discussed earlier that values for lattice enthalpy are positive values as the lattice is being broken. Essentially this is lattice dissociation enthalpy and is an endothermic process.Lattice formation enthalpy will give a negative value which has been calculated using the Born-Haber cycles. This gives us the energy released when a lattice is formed from its scattered gaseous ions.
