12.1.1 Emission Spectra & First Ionisation Energy

Emission Spectra

• Electrons move rapidly around the nucleus in energy shells
• Heat or electricity can be used to excite an electron to a higher main energy level
• These range from n = 1 (ground state) to n = ∞
• When the electrons 'fall' back down they must lose the energy difference between the two energy levels. This loss of energy is performed by releasing electromagnetic energy in the form of infrared, visible light or ultraviolet radiation.
• When the electron falls back to n = 1 (ground state) the energy released is in the ultraviolet region of the spectrum
• This corresponds to the Lyman series

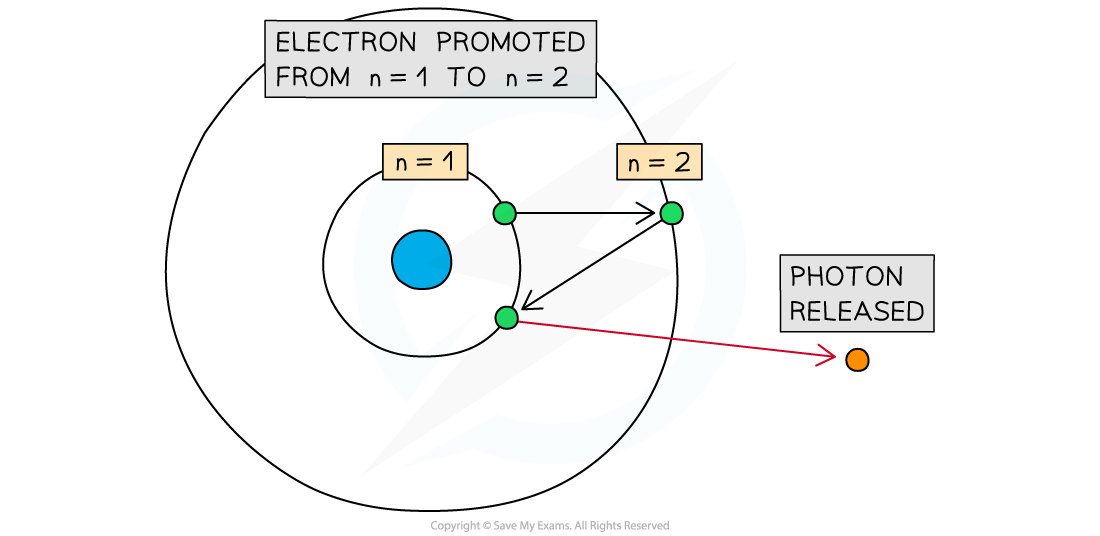
Promotion of an electron from the ground state (n=1) to n=2

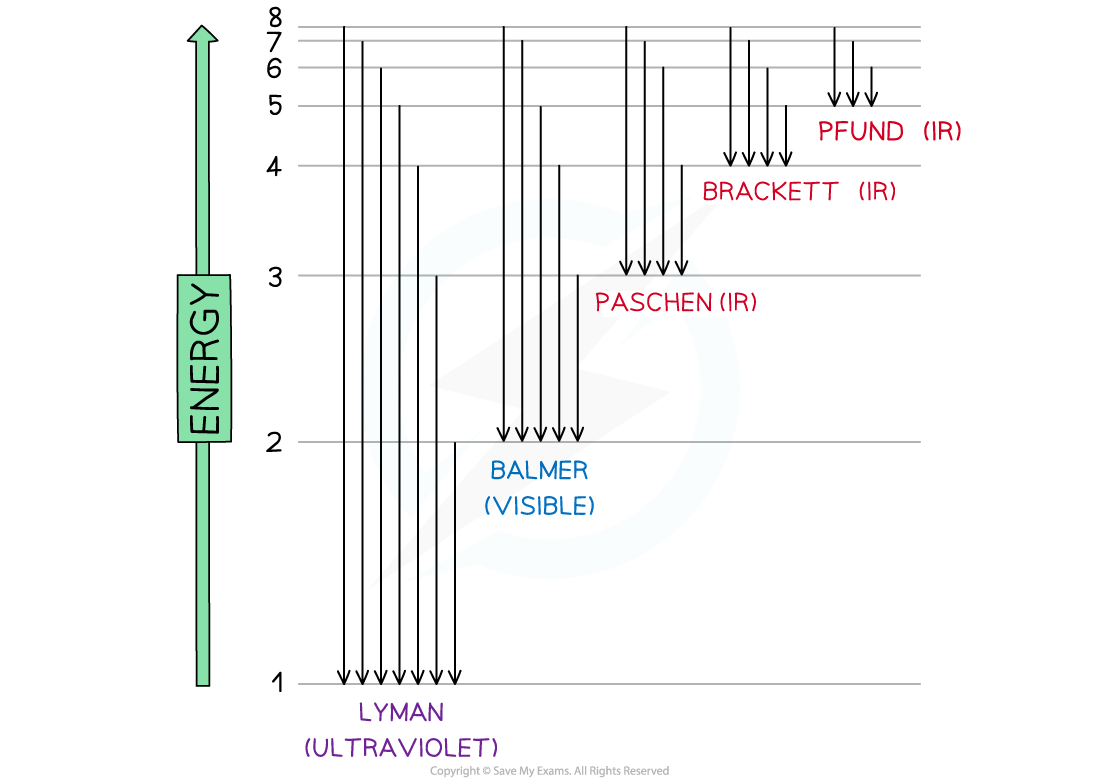
Electron jumps in the hydrogen spectrum

• This gives evidence for Bohr's model which is the idea that electrons exist in discrete energy levels so an exact amount of energy is required for an electron to 'jump' an energy level, a little like a ladder
• There are however limitations to this model
  • Assumes positions of electrons are fixed
  • Assumes energy levels are spherical in nature
  • Bohr limited calculations to hydrogen only, so does not explain the line spectra of other elements containing more than one electron

The Limit of Convergence

• As the line spectra is produced the lines will become closer together 
  • Where the lines appear to meet is called the limit of convergence
  • The convergence limit is the frequency at which the spectral lines converge
  • The energy required for an electron to escape the atom, or reach the upper limit of convergence, is the ionisation energy
  • The frequency of the radiation in the emission spectrum at the limit of convergence can be used to determine the first ionisation energy or IE₁
  • In the Lyman series for the hydrogen atom (UV region), the frequency at the limit of convergence relates to the energy given out when an electron falls from n = ∞ to n = 1
  • For hydrogen, the lines converge to a limit with a wavelength of 91.16 nm or 91.16 × 10⁻⁹ m

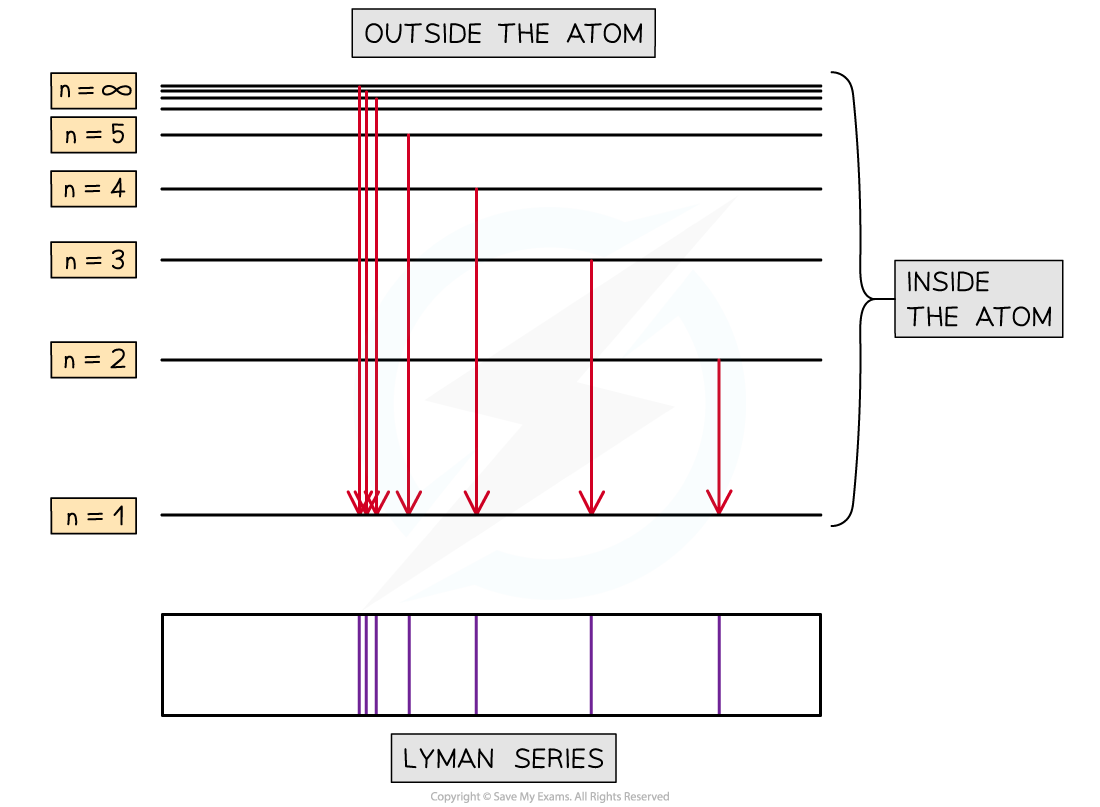
Lyman series (ultra-violet radiation) corresponds to transitions between higher shells and the ground state (n=1)

Calculating First Ionisation Energy

• When dealing with the Lyman series the largest transitions represent the fall from the infinite level to n=1
• In reverse, it can be considered to be equal to the ionisation energy (note that ionisation energy is given per mole of atoms)
• Therefore, the first ionisation energy (IE₁) of an atom can be calculated using the frequency (or wavelength) of the convergence limit
• We can do this by using the following equations

ΔE = h ν

c = ν λ

• In order to calculate first ionisation energy (IE₁) we must first calculate the frequency using the given data and rearranging:

c = ν λ

as

ν = c ÷ λ

• Once we know the frequency, we can use this to calculate the ionisation energy

Answer:

Step 1: Write out the equation to calculate the first ionisation energy (IE₁)

ΔE = h ν

Step 2: Substitute in numbers from question and data booklet to give energy change per atom

          IE₁ = 6.63 × 10⁻³⁴ × 1.24 × 10¹⁵

          IE₁ = 8.22 × 10⁻¹⁹ J atom⁻¹

Step 3: Calculate the first ionisation energy per mole by multiplying by Avogadro's constant

          IE₁ = 8.22 × 10^{−19  ×} 6.02 × 10²³

          IE₁ = 494 916 J mol⁻¹

Step 4: Convert J mol⁻¹ to kJ mol⁻¹ by dividing by 1000

          IE₁ = 495 kJ mol⁻¹

So the first ionisation energy (IE₁) of sodium has been calculated as 495 kJ mol⁻¹

Answer:

Step 1: Calculate the frequency of the convergence limit, converting wavelength into m (nm to m = × 10⁻⁹)

          c = ν λ

          ν = c ÷ λ

          ν = 3.00 × 10⁸ ÷ 91.16 × 10⁻⁹

          ν = 3.29 × 10¹⁵ s⁻¹

Step 2: Substitute into the equation to calculate IE₁ for one atom of hydrogen in J mol⁻¹ 

ΔE = h ν

         IE₁ = 6.63 × 10⁻³⁴ × 3.29 × 10¹⁵

         IE₁ = 2.18 × 10^-18 J atom⁻¹

Step 3: Calculate IE₁ for 1 mole of hydrogen atoms

          IE₁ = 2.18 × 10⁻¹⁸  × 6.02 × 10²³

          IE₁ = 1 313 491 J mol⁻¹

Step 4: Convert J mol⁻¹ to kJ mol⁻¹

          IE₁ = 1313 kJ mol⁻¹

So the first ionisation energy (IE₁) of hydrogen has been calculated as 1313 kJ mol⁻¹