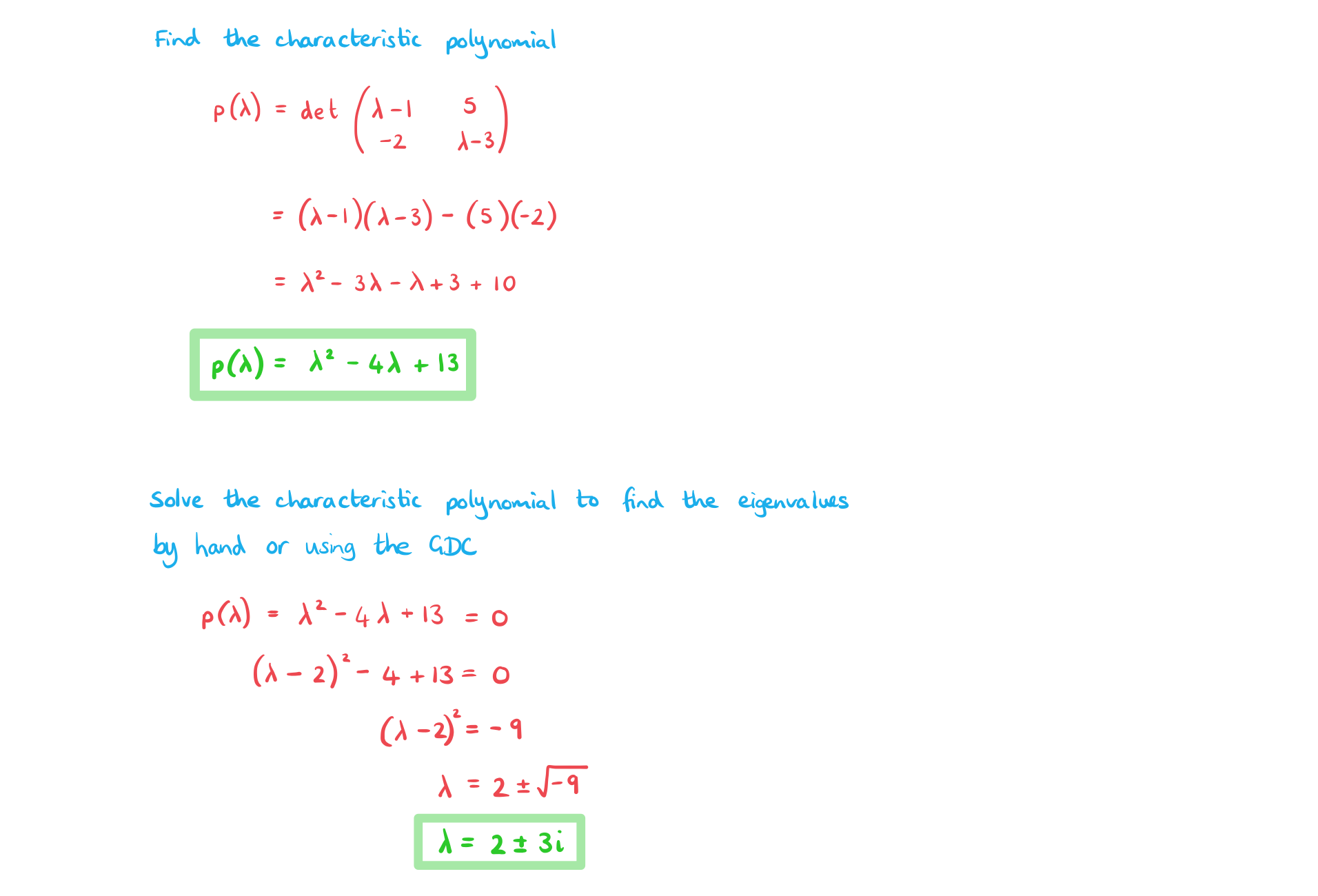1.8.1 Eigenvalues & Eigenvectors

Characteristic Polynomials

Eigenvalues and eigenvectors are properties of square matrices and are used in a lot of real-life applications including geometrical transformations and probability scenarios. In order to find these eigenvalues and eigenvectors, the characteristic polynomial for a matrix must be found and solved.

What is a characteristic polynomial?

For a matrix $A$ , if $A x = λ x$ when $x$ is a non-zero vector and $λ$ a constant, then $λ$ is an eigenvalue of the matrix $A$ and $x$ is its corresponding eigenvector
If $A x = λ x \Rightarrow (λ I - A) x = 0$ or $(A - λ I) x = 0$ and for $x$ to be a non-zero vector, $\det (λ I - A) = 0$
The characteristic polynomial of an $n \times n$ matrix is:

$p (λ) = \det (λ I - A)$

In this course you will only be expected to find the characteristic equation for a $2 \times 2$ matrix and this will always be a quadratic

How do I find the characteristic polynomial?

STEP 1
Write $λ I - A$ , remembering that the identity matrix must be of the same order as $A$
STEP 2
Find the determinant of $λ I - A$ using the formula given to you in the formula booklet

$\det A = | A | = a d - b c$

STEP 3
Re-write as a polynomial

Exam Tip

You need to remember the characteristic equation as it is not given in the formula booklet

Worked Example

Find the characteristic polynomial of the following matrix

$A = (\begin{matrix} 5 & 4 \\ 3 & 1 \end{matrix})$ .

1-8-1-ib-ai-hl-eigenvalues--eigenvectors-we-1-solution

Eigenvalues & Eigenvectors

How do you find the eigenvalues of a matrix?

The eigenvalues of matrix $A$ are found by solving the characteristic polynomial of the matrix
For this course, as the characteristic polynomial will always be a quadratic, the polynomial will always generate one of the following:

two real and distinct eigenvalues,
one real repeated eigenvalue or
complex eigenvalues

How do you find the eigenvectors of a matrix?

A value for $x$ that satisfies the equation is an eigenvector of matrix $A$
Any scalar multiple of $x$ will also satisfy the equation and therefore there an infinite number of eigenvectors that correspond to a particular eigenvalue
STEP 1
Write $x = (\begin{matrix} x \\ y \end{matrix})$
STEP 2
Substitute the eigenvalues into the equation $(λ I - A) x = 0$ , and form two equations in terms of $x$ and $y$
STEP 3
There will be an infinite number of solutions to the equations, so choose one by letting one of the variables be equal to $1$ and using that to find the other variable

Exam Tip

You can do a quick check to on your calculated eigenvalues as the values along the leading diagonal of the matrix you are analysing should sum to the total of the eigenvalues for the matrix

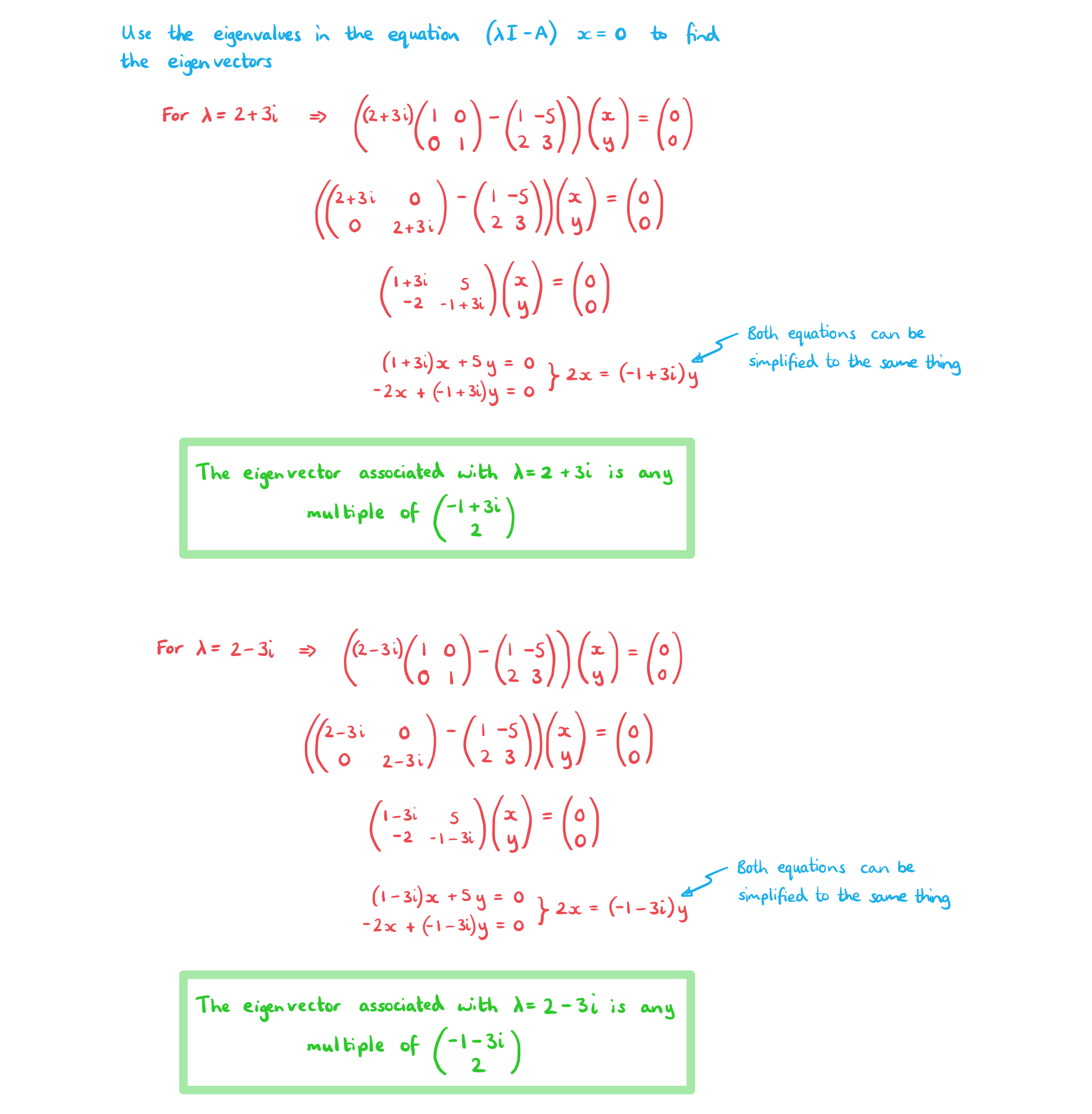
Worked Example

Find the eigenvalues and associated eigenvectors for the following matrices.

A = (\begin{matrix} 5 & 4 \\ 3 & 1 \end{matrix})

1-8-1-ib-ai-hl-eigenvalues--eigenvectors-we-2ai-solution

1-8-1-ib-ai-hl-eigenvalues--eigenvectors-we-2aii-solution

B = (\begin{matrix} 1 & - 5 \\ 2 & 3 \end{matrix})

1-8-1-ib-ai-hl-eigenvalues--eigenvectors-we-2bi-solution

1-8-1-ib-ai-hl-eigenvalues--eigenvectors-we-2bii-solution

DP IB Maths: AI HL

Revision Notes

1.8.1 Eigenvalues & Eigenvectors

Characteristic Polynomials

What is a characteristic polynomial?

How do I find the characteristic polynomial?

Exam Tip

Worked Example

Eigenvalues & Eigenvectors

How do you find the eigenvalues of a matrix?

How do you find the eigenvectors of a matrix?

Exam Tip

Worked Example

Author: Naomi

Resources

Members

Company

Quick Links