3.9.2 Constant & Variable Velocity

Vectors & Constant Velocity

How are vectors used to model linear motion?

If an object is moving with constant velocity it will travel in a straight line
For an object moving in a straight line in two or three dimensions its velocity, displacement and time can be related using the vector equation of a line

r = a + λb
Letting

r be the position of the object at the time, t
a be the position vector, r₀ at the start (t = 0)
$λ$ represent the time, t
b be the velocity vector, v

Then the position of the object at the time, t can be given by

r = r₀+ tv

The velocity vector is the direction vector in the equation of the line
The speed of the object will be the magnitude of the velocity |v|

Worked Example

A car, moving at constant speed, takes 2 minutes to drive in a straight line from point A (-4, 3) to point B (6, -5).

At time t, in minutes, the position vector (p) of the car relative to the origin can be given in the form $p = a + t b$ .

Find the vectors a and b.

3-10-2-ib-aa-hl-kinematics-vectors-we-solution

Vectors & Variable Velocity

How are vectors used to model motion with variable velocity?

The velocity of a particle is the rate of change of its displacement over time
In one dimension velocity, v, is found be taking the derivative of the displacement, s, with respect to time, t
- $v = \frac{d s}{d t}$
In more than one dimension vectors are used to represent motion
For displacement given as a function of time in the form
- $r (t) = (\binom{f_{1} (t)}{f_{2} (t)})$
The velocity vector can be found by differentiating each component of the vector individually
- $v = (\binom{v_{1} (t)}{v_{2} (t)})$
- $v = \frac{d r}{d t} = (\binom{f_{1}' (t)}{f_{2}' (t)})$
- The velocity should be left as a vector
- The speed is the magnitude of the velocity
If the velocity vector is known, displacement can be found by integrating each component of the vector individually
- The constant of integration for each component will need to be found
The acceleration of a particle is the rate of change of its velocity over time
In one dimension acceleration, a, is found be taking the derivative of the velocity, v, with respect to time, t
- $a = \frac{d v}{d t} = \frac{d^{2} r}{d t^{2}}$
In two dimensions acceleration can be found by differentiating each component of the velocity vector individually
- $a = (\binom{a_{1} (t)}{a_{2} (t)})$
- $a = \frac{d v}{d t} = (\binom{v_{1}' (t)}{v_{2}' (t)})$
- $a = \frac{d^{2} r}{d t^{2}} = (\binom{f_{1}'' (t)}{f_{2}'' (t)})$
If the acceleration vector is known, the velocity vector can be found by integrating each component of the acceleration vector individually
- The constant of integration for each component will need to be found

Exam Tip

Look out for clues in the question as to whether you should treat the question as a constant or variable velocity problem
- 'moving at a constant speed' will imply using a linear model
- an object falling or rolling would imply variable velocity

Worked Example

A ball is rolling down a hill with velocity $v = (5 3) + t (0 - 0.8)$ . At the time t = 0 the coordinate of the ball are (3, -2).

Find the acceleration vector of the ball's motion.

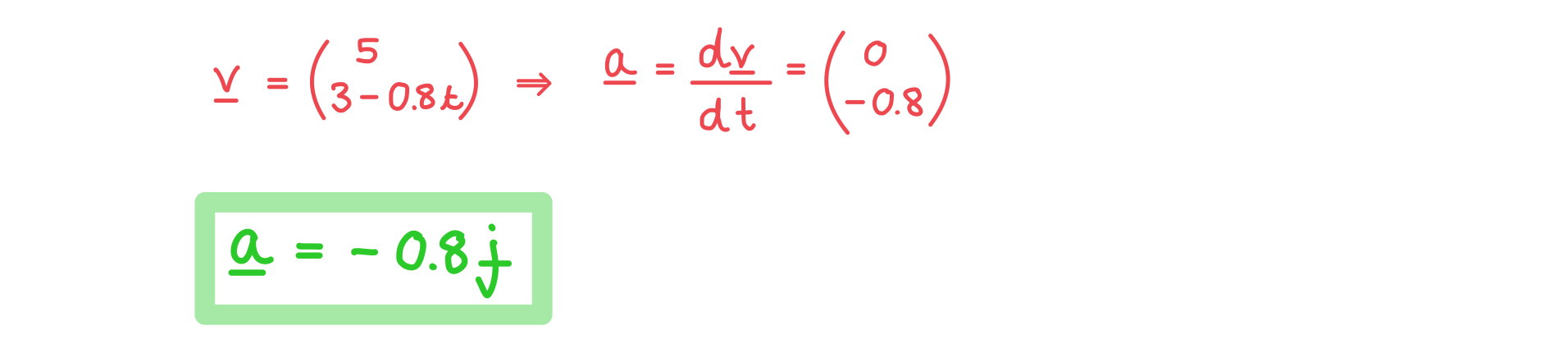
3-9-2-ib-ai-hl-variable-velocity-we-solution-a

Find the position vector of the ball at the time, t.

3-9-2-ib-ai-hl-variable-velocity-we-solution-b

DP IB Maths: AI HL

Revision Notes

3.9.2 Constant & Variable Velocity

Vectors & Constant Velocity

How are vectors used to model linear motion?

Worked Example

Vectors & Variable Velocity

How are vectors used to model motion with variable velocity?

Exam Tip

Worked Example

Author: Amber

Resources

Members

Company

Quick Links