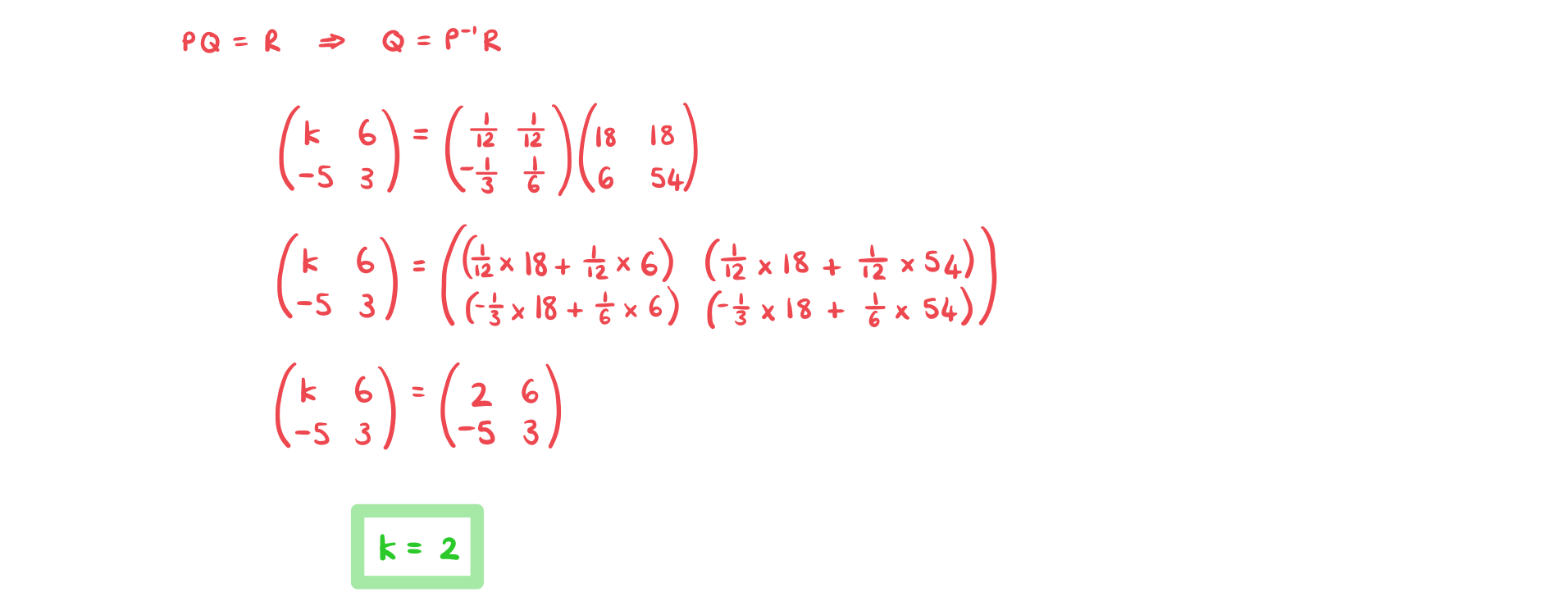Determinants
What is a determinant?
- The determinant is a numerical value (positive or negative) calculated from the elements in a matrix and is used to find the inverse of a matrix
- You can only find the determinant of a square matrix
- The method for finding the determinant of a
matrix is given in your formula booklet:
- You only need to be able to find the determinant of a
matrix by hand
- For larger
matrices you are expected to use your GDC
- The determinant of an identity matrix is
- The determinant of a zero matrix is
- When finding the determinant of a multiple of a matrix or the product of two matrices:
(for a
matrix)
Worked Example
Consider the matrix , where
is a constant.
a)
Given that format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2211.5%22%20y%3D%2216%22%3Edet%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20font-weight%3D%22bold%22%20text-anchor%3D%22middle%22%20x%3D%2233.5%22%20y%3D%2216%22%3EA%3C%2Ftext%3E%3Ctext%20font-family%3D%22math143f4d31b04031e49f5eb18baba%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2249.5%22%20y%3D%2216%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22math143f4d31b04031e49f5eb18baba%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2266.5%22%20y%3D%2216%22%3E%26%23x2212%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2279.5%22%20y%3D%2216%22%3E3%3C%2Ftext%3E%3C%2Fsvg%3E) , find the value of
, find the value of  .
.

b)
Find the determinant of  .
.

Inverse Matrices
How do I find the inverse of a matrix?
- The determinant can be used to find out if a matrix is invertible or not:
- If
, then
is invertible
- If
, then
is singular and does not have an inverse
- If
- The method for finding the inverse of a
matrix is given in your formula booklet:
- You only need to be able to find the inverse of a
matrix by hand
- For larger
matrices you are expected to use your GDC
- The inverse of a square matrix
is the matrix
such that the product of these matrices is an identity matrix,
- As a result of this property:
(pre-multiplying by
)
(post-multiplying by
)
- As a result of this property:
Worked Example
Consider the matrices ,
and
, where
is a constant.
a)
Find format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20font-weight%3D%22bold%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2217%22%3EP%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1da40657c9fece7e48d30af42d3%22%20font-size%3D%2212%22%20text-anchor%3D%22middle%22%20x%3D%2217.5%22%20y%3D%2212%22%3E%26%23x2212%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2213%22%20text-anchor%3D%22middle%22%20x%3D%2225.5%22%20y%3D%2212%22%3E1%3C%2Ftext%3E%3C%2Fsvg%3E) .
.

b)
Given that format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20font-weight%3D%22bold%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2216%22%3EP%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20font-weight%3D%22bold%22%20text-anchor%3D%22middle%22%20x%3D%2218.5%22%20y%3D%2216%22%3EQ%3C%2Ftext%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2234.5%22%20y%3D%2216%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20font-weight%3D%22bold%22%20text-anchor%3D%22middle%22%20x%3D%2249.5%22%20y%3D%2216%22%3ER%3C%2Ftext%3E%3C%2Fsvg%3E) find the value of
find the value of  .
.