Logarithmic Functions & Graphs
What are the key features of logarithmic graphs?
- A logarithmic function is of the form
- Remember the natural logarithmic function
- This is the inverse of
and
- The graphs do not have a y-intercept
- The graphs have a vertical asymptote at the y-axis:
- The graphs have one root at
- This can be found using your GDC
- The graphs do not have any minimum or maximum points
- The value of b determines whether the graph is increasing or decreasing
- If b is positive then the graph is increasing
- If b is negative then the graph is decreasing
- This is the inverse of
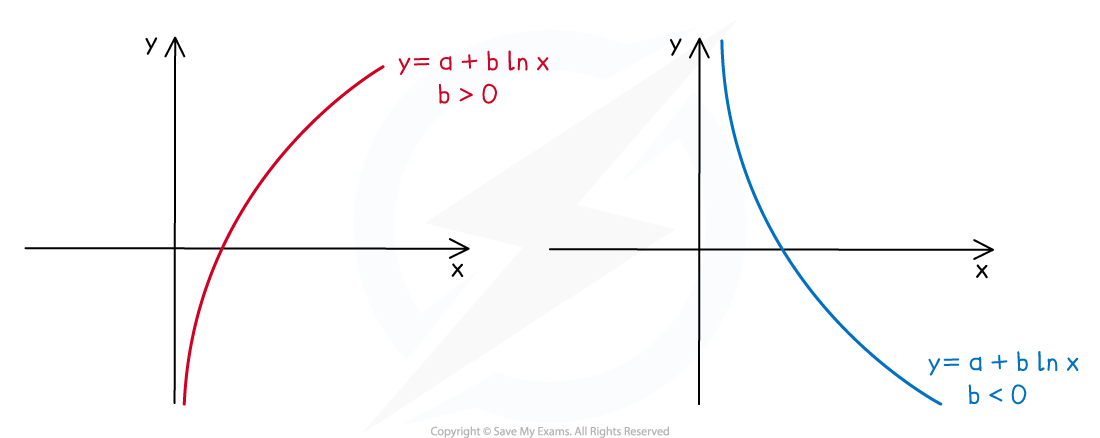
Logistic Functions & Graphs
What are the key features of logistic graphs?
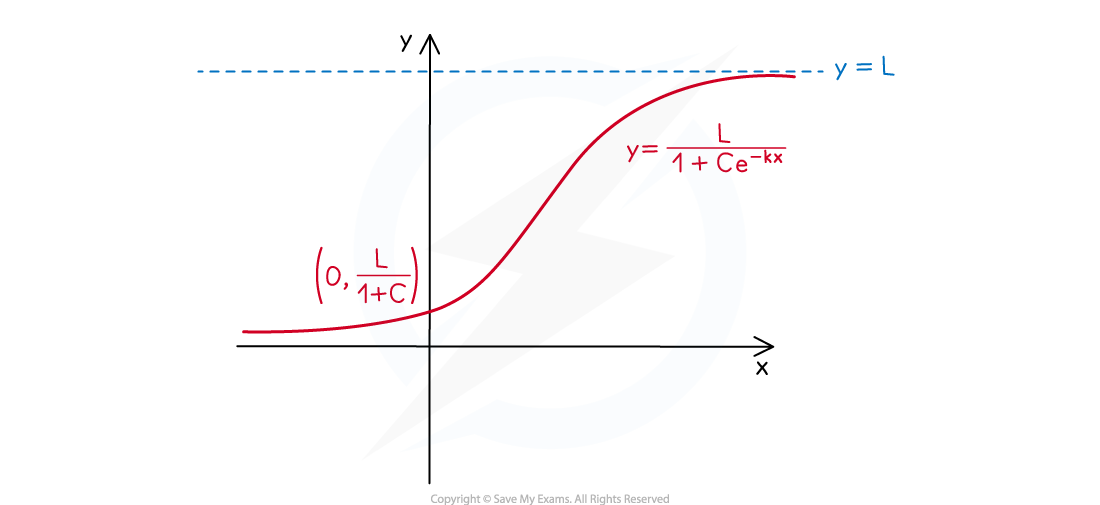
- A logistic function is of the form
- L, C & k are positive constants
- Its domain is the set of all real values
- Its range is the set of real positive values less than L
- The y-intercept is at the point
- There are no roots
- There is a horizontal asymptote at y = L
- This is called the carrying capacity
- This is the upper limit of the function
- For example: it could represent the limit of a population size
- There is a horizontal asymptote at y = 0
- The graph is always increasing