5.7.2 Second Order Differential Equations

Euler's Method: Second Order

How do I apply Euler’s method to second order differential equations?

A second order differential equation is a differential equation containing one or more second derivatives
In this section of the course we consider second order differential equations of the form

$\frac{d^{2} x}{d t^{2}} = f (x, \frac{d x}{d t}, t)$

You may need to rearrange the differential equation given to get it in this form

In order to apply Euler’s method, use the substitution $y = \frac{d x}{d t}$ to turn the second order differential equation into a pair of coupled first order differential equations

If $y = \frac{d x}{d t}$ , then $\frac{d y}{d t} = \frac{d^{2} x}{d t^{2}}$
This changes the second order differential equation into the coupled system

Approximate solutions to this coupled system can then be found using the standard Euler’s method for coupled systems
- See the notes on this method in the revision note 5.6.4 Approximate Solutions to Differential Equations

$\frac{d x}{d t} = y \frac{d y}{d t} = f (x, y, t))$

Worked Example

Consider the second order differential equation $\frac{d^{2} x}{d t^{2}} + 2 \frac{d x}{d t} + x = 50 \cos t$ .

Show that the equation above can be rewritten as a system of coupled first order differential equations.

5-7-2-ib-ai-hl-eulers-method-second-order-a-we-solution

Initially

x = 2

and

\frac{d x}{d t} = - 1

. By applying Euler’s method with a step size of 0.1, find approximations for the values of x and

\frac{d x}{d t}

when t = 0.5 .

5-7-2-ib-ai-hl-eulers-method-second-order-b-we-solution

Exact Solutions & Phase Portraits: Second Order

How can I find the exact solution for a second order differential equation?

In some cases we can apply methods we already know to find the exact solutions for second order differential equations
In this section of the course we consider second order differential equations of the form

$\frac{d^{2} x}{d t^{2}} + a \frac{d x}{d t} + b x = 0$

- are constants
Use the substitution $y = \frac{d x}{d t}$ to turn the second order differential equation into a pair of coupled first order differential equations
- If $y = \frac{d x}{d t}$ , then $\frac{d y}{d t} = \frac{d^{2} x}{d t^{2}}$
- This changes the second order differential equation into the coupled system

$\begin{array}{rcl} \frac{d x}{d t} & = & y \\ \frac{d y}{d t} & = & - b x - a y \end{array}$

- The coupled system may also be represented in matrix form as

$(\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}) = (\begin{matrix} 0 & 1 \\ - b & - a \end{matrix}) (\begin{matrix} x \\ y \end{matrix})$

In the ‘dot notation’ here and

That can be written even more succinctly as $\dot{x} = M x$

Here $\dot{x} = (\begin{matrix} \dot{x} \\ \dot{y} \end{matrix})$ , $x = (\begin{matrix} x \\ y \end{matrix})$ , and $M = (\begin{matrix} 0 & 1 \\ - b & - a \end{matrix})$

Once the original equation has been rewritten in matrix form, the standard method for finding exact solutions of systems of coupled differential equations may be used

The solutions will depend on the eigenvalues and eigenvectors of the matrix M
For the details of the solution method see the revision note 5.7.1 Coupled Differential Equations
Remember that exam questions will only ask for exact solutions for cases where the eigenvalues of M are real and distinct

How can I use phase portraits to investigate the solutions to second order differential equations?

Here we are again considering second order differential equations of the form

$\frac{d^{2} x}{d t^{2}} + a \frac{d x}{d t} + b x = 0$

a & b are real constants

As shown above, the substitution $y = \frac{d x}{d t}$ can be used to convert this second order differential equation into a system of coupled first order differential equations of the form $\dot{x} = M x$

Here $\dot{x} = (\begin{matrix} \dot{x} \\ \dot{y} \end{matrix})$ , $x = (\begin{matrix} x \\ y \end{matrix})$ , and $M = (\begin{matrix} 0 & 1 \\ - b & - a \end{matrix})$

Once the equation has been rewritten in this form, you may use the standard methods to construct a phase portrait or sketch a solution trajectory for the equation

For the details of the phase portrait and solution trajectory methods see the revision note 5.7.1 Coupled Differential Equations
When interpreting a phase portrait or solution trajectory sketch, don’t forget that $y = \frac{d x}{d t}$

So if x represents the displacement of a particle, for example, then $y = \frac{d x}{d t}$ will represent the particle’s velocity

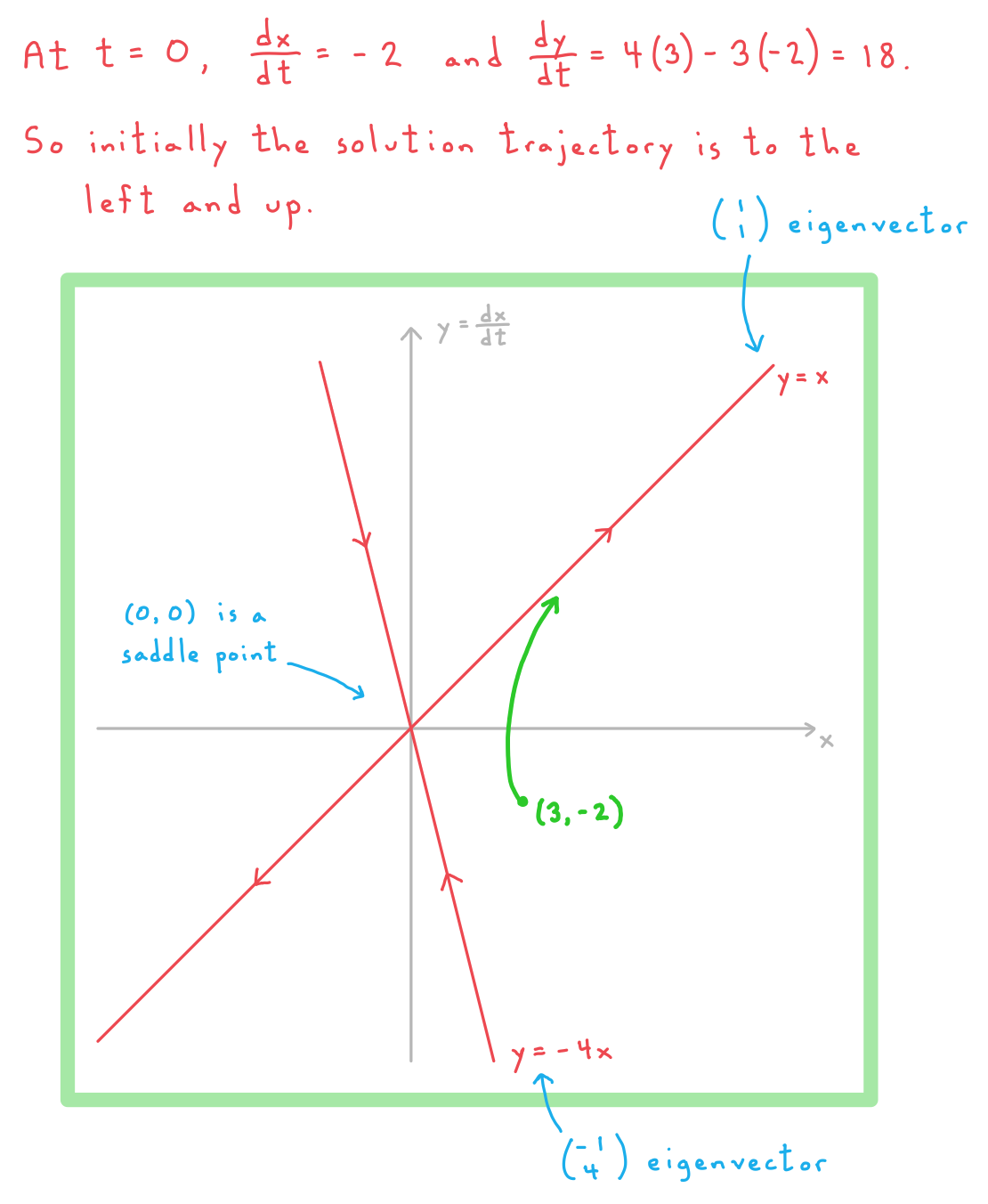
Worked Example

Consider the second order differential equation $\frac{d^{2} x}{d t^{2}} + 3 \frac{d x}{d t} - 4 x = 0$ . Initially x = 3 and $\frac{d x}{d t} = - 2$ .

Show that the equation above can be rewritten as a system of coupled first order differential equations.

5-7-2-ib-ai-hl-exact-second-order-a-we-solution

Given that the matrix

(\begin{matrix} 0 & 1 \\ 4 & - 3 \end{matrix})

has eigenvalues of 1 and -4 with corresponding eigenvectors

(\begin{matrix} 1 \\ 1 \end{matrix})

and

(\begin{matrix} - 1 \\ 4 \end{matrix})

, find the exact solution to the second order differential equation.

5-7-2-ib-ai-hl-exact-second-order-b-we-solution

Sketch the trajectory of the solution to the equation on a phase diagram, showing the relationship between x and

\frac{d x}{d t}

5-7-2-ib-ai-hl-exact-second-order-c-we-solution

DP IB Maths: AI HL

Revision Notes

5.7.2 Second Order Differential Equations

Euler's Method: Second Order

How do I apply Euler’s method to second order differential equations?

Worked Example

Exact Solutions & Phase Portraits: Second Order

How can I find the exact solution for a second order differential equation?

How can I use phase portraits to investigate the solutions to second order differential equations?

Worked Example

Author: Roger

Resources

Members

Company

Quick Links