2.2.3 Properties of Graphs

Quadratic Functions & Graphs

What are the key features of quadratic graphs?

A quadratic graph is of the form $y = a x^{2} + b x + c$ where $a \neq 0$ .
The value of a affects the shape of the curve
- If a is positive the shape is $\cup$
- If a is negative the shape is $\cap$
The y-intercept is at the point (0, c)
The zeros or roots are the solutions to $a x^{2} + b x + c = 0$
- These can be found using your GDC or the quadratic formula
- These are also called the x-intercepts
- There can be 0, 1 or 2 x-intercepts
There is an axis of symmetry at $x = - \frac{b}{2 a}$
- This is given in your formula booklet
- If there are two x-intercepts then the axis of symmetry goes through the midpoint of them
The vertex lies on the axis of symmetry
- The x-coordinate is $- \frac{b}{2 a}$
- The y-coordinate can be found using the GDC or by calculating y when $x = - \frac{b}{2 a}$
- If a is positive then the vertex is the minimum point
- If a is negative then the vertex is the maximum point

Quadratic Graphs Notes Diagram 1

Exam Tip

Use your GDC to find the roots and the turning point of a quadratic function
- You do not need to factorise or complete the square
- It is good exam technique to sketch the graph from your GDC as part of your working

Worked Example

Write down the equation of the axis of symmetry for the graph

y = 4 x^{2} - 4 x - 3

2-2-3-ib-ai-sl-quad--cub-graphs-a-we-solution

Sketch the graph

y = 4 x^{2} - 4 x - 3

2-2-3-ib-ai-sl-quad--cub-graphs-b-we-solution

Cubic Functions & Graphs

What are the key features of cubic graphs?

A cubic graph is of the form $y = a x^{3} + b x^{2} + c x + d$ where $a \neq 0$ .
The value of a affects the shape of the curve
- If a is positive the graph goes from bottom left to top right
- If a is negative the graph goes from top left to bottom right
The y-intercept is at the point (0, d)
The zeros or roots are the solutions to $a x^{3} + b x^{2} + c x + d = 0$
- These can be found using your GDC
- These are also called the x-intercepts
- There can be 1, 2 or 3 x-intercepts
  - There is always at least 1
There are either 0 or 2 local minimums/maximums
- If there are 0 then the curve is monotonic (always increasing or always decreasing)
- If there are 2 then one is a local minimum and one is a local maximum

Sketching Polynomials Notes Diagram 1

Exam Tip

Use your GDC to find the roots, the local maximum and local minimum of a cubic function
When drawing/sketching the graph of a cubic function be sure to label all the key features
- $x$ and $y$ axes intercepts
- the local maximum point
- the local minimum point

Worked Example

Sketch the graph $y = 2 x^{3} - 6 x^{2} + x - 3$ .

2-2-3-ib-ai-sl-quad--cub-graphs-c-we-solution

Exponential Functions & Graphs

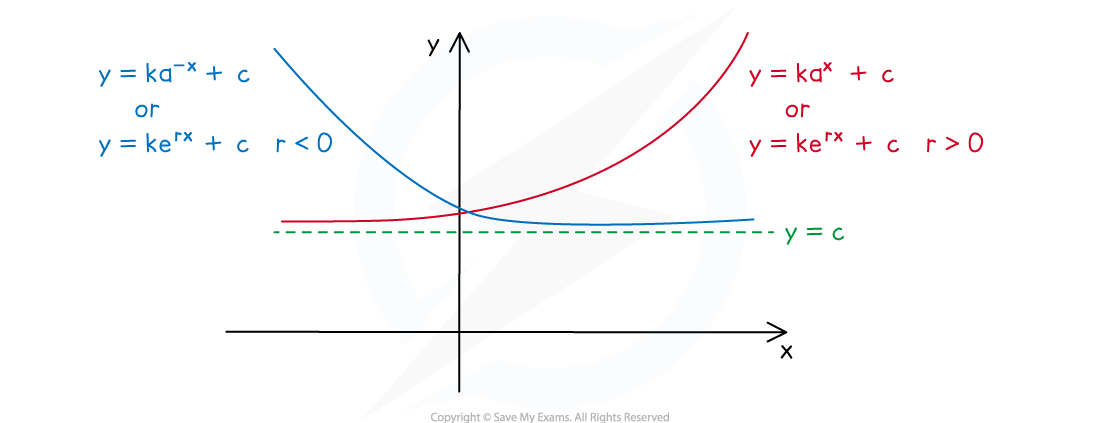
What are the key features of exponential graphs?

An exponential graph is of the form
- $y = k a^{x} + c$ or $y = k a^{- x} + c$ where $a > 0$
- $y = k e^{r x} + c$
  - Where e is the mathematical constant 2.718…
The y-intercept is at the point (0, k + c)
There is a horizontal asymptote at y = c
The value of k determines whether the graph is above or below the asymptote
- If k is positive the graph is above the asymptote
  - So the range is $y > c$
- If k is negative the graph is below the asymptote
  - So the range is $y < c$
The coefficient of x and the constant k determine whether the graph is increasing or decreasing
- If the coefficient of x and k have the same sign then graph is increasing
- If the coefficient of x and k have different signs then the graph is decreasing
There is at most 1 root
- It can be found using your GDC

ib-ai-sl-2-2-3-exponential-graphs

Exam Tip

You may have to change the viewing window settings on your GDC to make asymptotes clear
- A small scale can make it look as though the curve and an asymptote intercept
Be careful about how two exponential graphs drawn on the same axes look
- Particularly which one is "on top" either side of the $y$ -axis

Worked Example

On the same set of axes sketch the graphs

y = 2^{x}

and

y = 3^{x}

. Clearly label each graph.

2-2-3-ib-ai-sl-exp-graphs-a-we-solution

Sketch the graph

y = 2 e^{- 3 x} + 1

2-2-3-ib-ai-sl-exp-graphs-b-we-solution

Sinusoidal Functions & Graphs

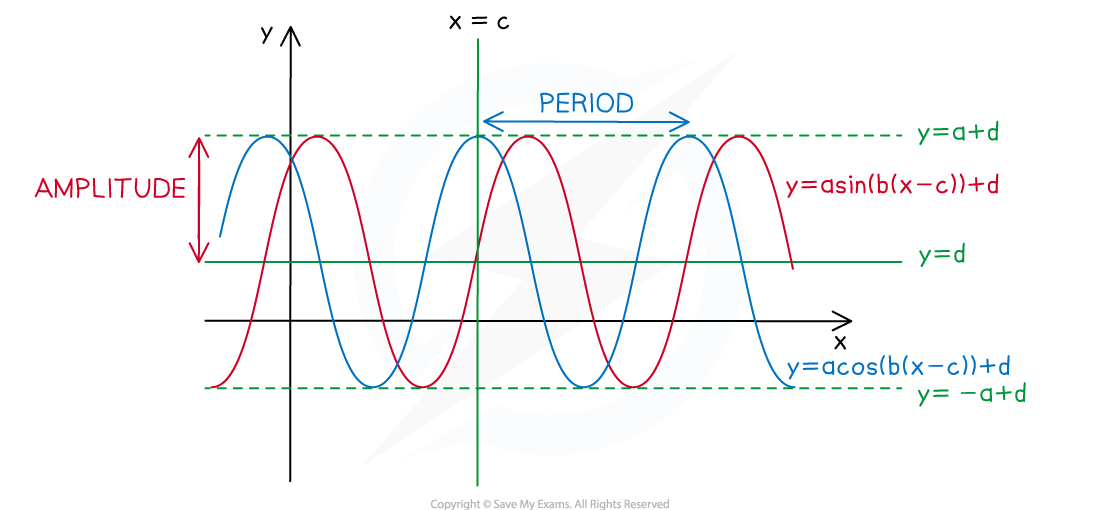
What are the key features of sinusoidal graphs?

A sinusoidal graph is of the form
- $y = a \sin (b (x - c)) + d$
- $y = a \cos (b (x - c)) + d$
The y-intercept is at the point where x = 0
- (0, -asin(bc) + d) for $y = a \sin (b (x - c)) + d$
- (0, acos(bc) + d) for $y = a \cos (b (x - c)) + d$
The period of the graph is the length of the interval of a full cycle
- This is $\frac{360 °}{b}$ (in degrees) or $\frac{2 π}{b}$
The maximum value is y = a + d
The minimum value is y = -a + d
The principal axis is the horizontal line halfway between the maximum and minimum values
- This is y = d
The amplitude is the vertical distance from the principal axis to the maximum value
- This is a
The phase shift is the horizontal distance from its usual position
- This is c

Exam Tip

Make sure your angle setting is in the correct mode (degrees or radians) at the start of a question involving sinusoidal functions
Pay careful attention to the angles between which you are required to use or draw/sketch a sinusoidal graph
- e.g. 0° ≤ x ≤ 360°

Worked Example

Sketch the graph

y = 3 \sin (2 (x ° - 15 °)) + 1

for the values

0 \leq x \leq 360

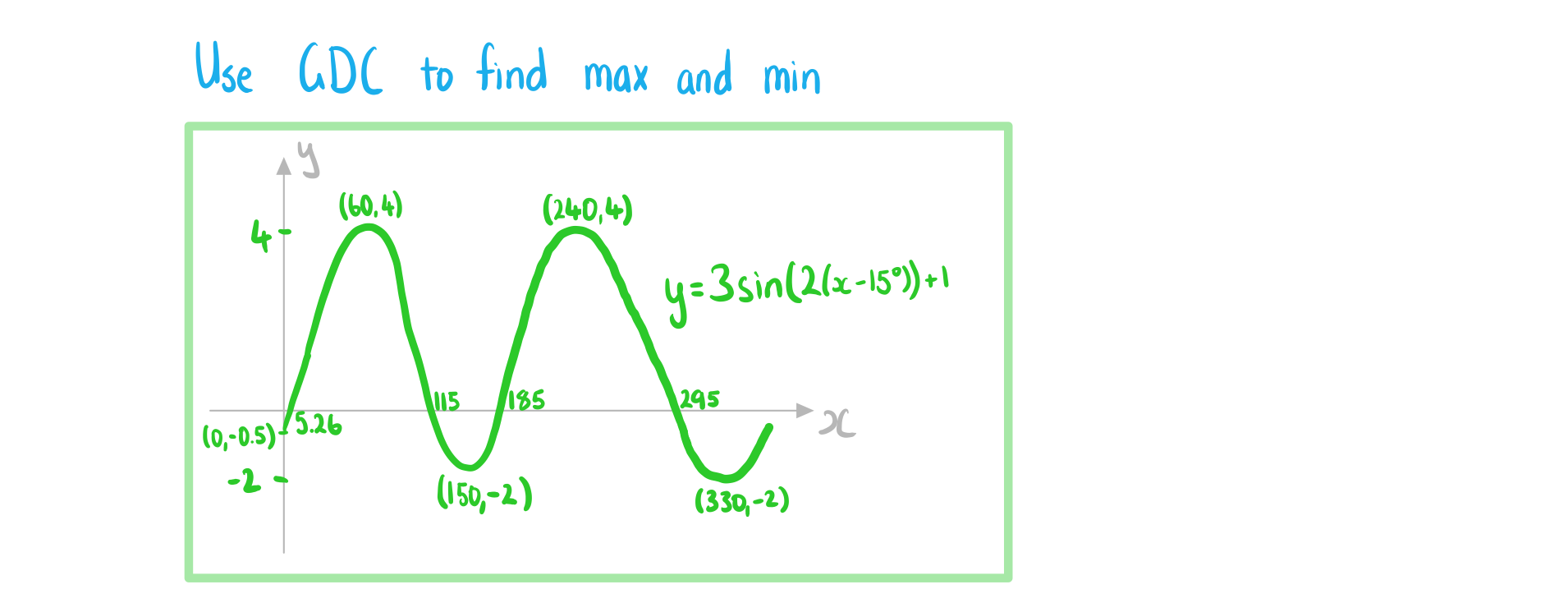
2-2-3-ib-ai-hl-sinusoidal-graphs-a-we-solution

State the equation of the principal axis of the curve.

2-2-3-ib-ai-sl-sinusoidal-graphs-b-we-solution

State the period and amplitude.

2-2-3-ib-ai-sl-sinusoidal-graphs-c-we-solution

DP IB Maths: AI HL

Revision Notes

2.2.3 Properties of Graphs

Quadratic Functions & Graphs

What are the key features of quadratic graphs?

Exam Tip

Worked Example

Cubic Functions & Graphs

What are the key features of cubic graphs?

Exam Tip

Worked Example

Exponential Functions & Graphs

What are the key features of exponential graphs?

Exam Tip

Worked Example

Sinusoidal Functions & Graphs

What are the key features of sinusoidal graphs?

Exam Tip

Worked Example

Author: Daniel

Resources

Members

Company

Quick Links