DP IB Maths: AI HL

Revision Notes

Home / IB / Maths: AI HL / DP / Revision Notes / 2. Functions / 2.6 Further Modelling with Functions / 2.6.2 Natural Logarithmic Models

2.6.2 Natural Logarithmic Models

Natural Logarithmic Models

What are the parameters of natural logarithmic models?

A natural logarithmic model is of the form $f (x) = a + b \ln x$
The a represents the value of the function when x = 1
The b determines the rate of change of the function

A bigger absolute value of b leads to a faster rate of change

What can be modelled as a natural logarithmic model?

A natural logarithmic model can be used when the variable increases rapidly for a period followed by a much slower rate of increase with no limiting value

M(I) is the magnitude of an earthquake with an intensity of I
d(I) is the decibels measured of a noise with an intensity of I

What are possible limitations a natural logarithmic model?

A natural logarithmic graph is unbounded

However in real-life the variable might have a limiting value

Worked Example

The sound intensity level, $L$ , in decibels (dB) can be modelled by the function

$L (I) = a + 8 \ln I$ ,

where $I$ is the sound intensity, in watts per square metre (Wm^-2).

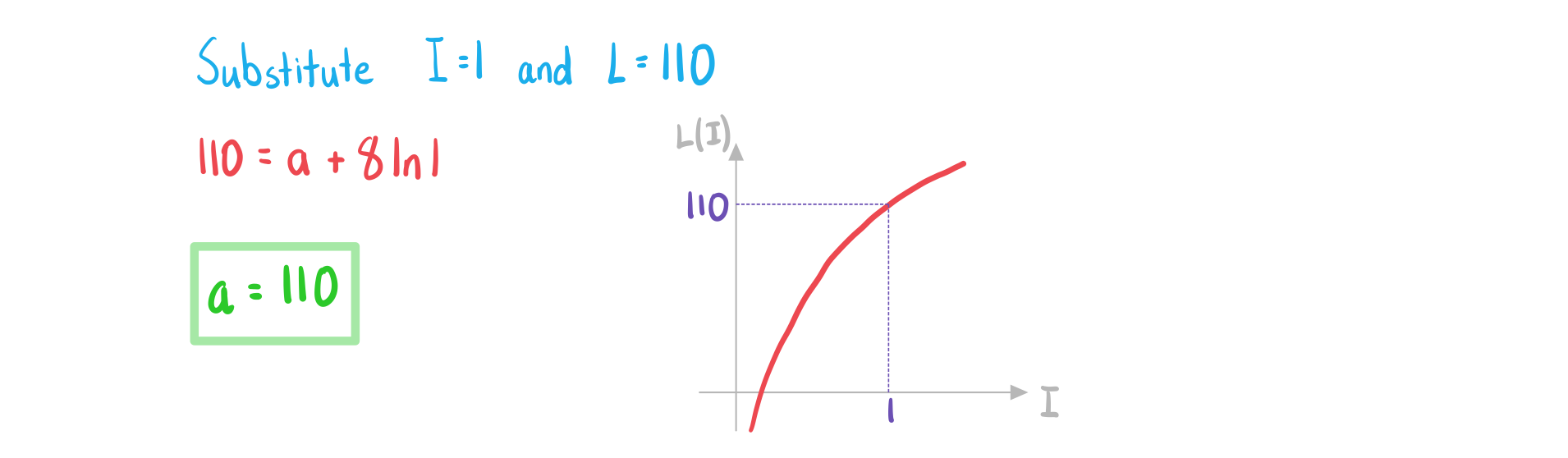
a)

Given that a sound intensity of 1 Wm^-2 produces a sound intensity level of 110 dB, write down the value of

a

.

2-6-2-ib-ai-hl-natural-log-model-a-we-solution

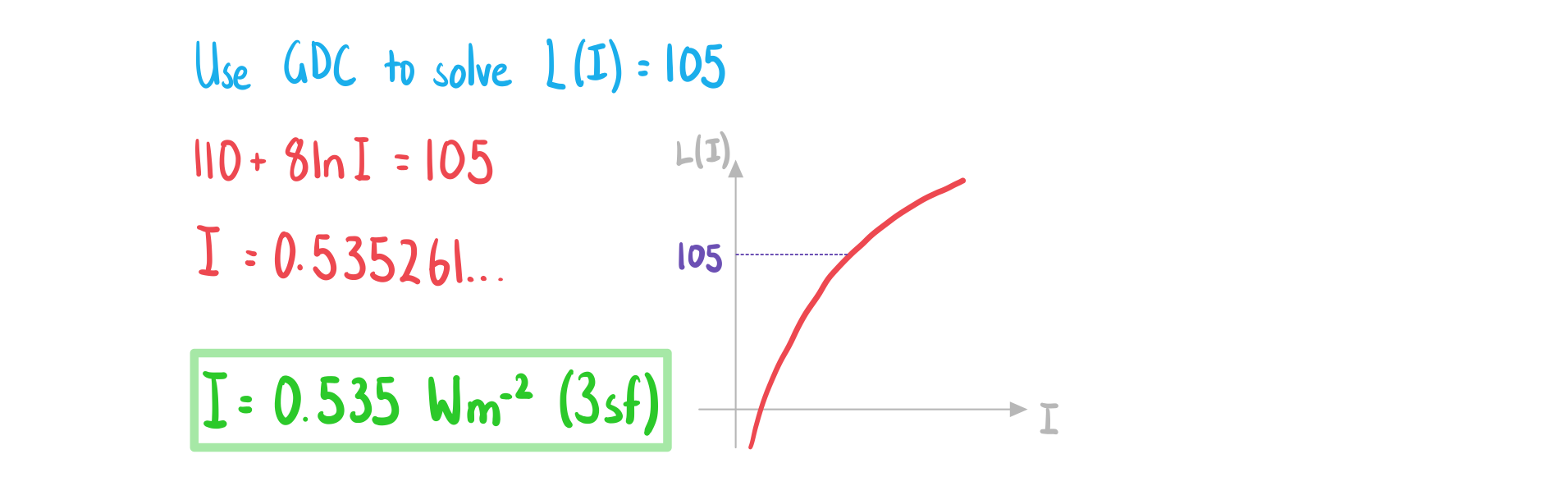
b)

Find the sound intensity, in Wm^-2, of a car alarm that has a sound intensity level of 105 dB.

2-6-2-ib-ai-hl-natural-log-model-b-we-solution

Daniel Finlay

Author: Daniel

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Resources

Home Join Support

Members

Members Home Account Logout

Company

About Us Contact Us Jobs Terms Privacy Facebook Twitter

Quick Links

GCSE Revision Notes IGCSE Revision Notes A Level Revision Notes Biology Chemistry Physics Maths 2022 Advance Information

© IB Documents (2) Team & u/aimlesskr
IBO was not involved in the production of, and does not endorse, the resources created by Save My Exams.