4.3.3 Linearising using Logarithms

Exponential Relationships

How do I use logarithms to linearise exponential relationships?

Graphs of exponential functions appear as straight lines on semi-log graphs
Suppose $y = a b^{x}$
- You can take logarithms of both sides
  - $\ln y = \ln (a b^{x})$
- You can split the right hand side into the sum of two logarithms
  - $\ln y = \ln a + \ln (b^{x})$
- You can bring down the power in the final term
  - $\ln y = \ln a + x \ln b$
$\ln y = \ln a + x \ln b$ is in linear form $Y = m X + c$
- $Y = \ln y$
- $X = x$
- $m = \ln b$
- $c = \ln a$

**How can I use linearised data to find the values of the parameters in an exponential model y = ab^x?**

STEP 1: Linearise the data using $Y = \ln y$ and $X = x$
STEP 2: Find the equation of the regression line of Y on X : $Y = m X + c$
STEP 3: Equate coefficients between $Y = m X + c$ and $\ln y = \ln a + x \ln b$
- $m = \ln b$
- $c = \ln a$
STEP 4: Solve to find a and b
- $a = e^{c}$
- $b = e^{m}$

Worked Example

Hatter has noticed that over the past 50 years there seems to be fewer hatmakers in London. He also knows that global temperatures have been rising over the same time period. He decides to see if there could be any correlation, so he collects data on the number of hatmakers and the global mean temperatures from the past 50 years and records the information in the graph below.

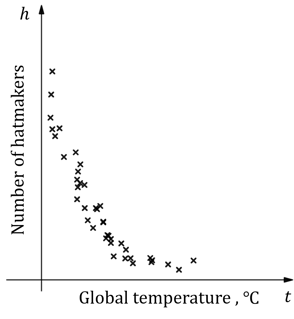
2-7-2-a-we-image

Hatter suggests that the equation for $h$ in terms of $t$ can be written in the form $h = a b^{t}$
. He linearises the data using $x = t$ and $y = \ln h$ and calculates the regression line of $y$ on $x$ to be $y = 4.382 - 1.005 x$ .

Find the values of $a$ and $b$ .

2-7-2-ib-ai-hl-exp-relationships-we-solution

Power Relationships

How do I use logarithms to linearise power relationships?

Graphs of power functions appear as straight lines on log-log graphs
Suppose $y = a x^{b}$
- You can take logarithms of both sides
  - $\ln y = \ln (a x^{b})$
- You can split the right hand side into the sum of two logarithms
  - $\ln y = \ln a + \ln (x^{b})$
- You can bring down the power in the final term
  - $\ln y = \ln a + b \ln x$
$\ln y = \ln a + b \ln x$ is in linear form $Y = m X + c$
- $Y = \ln y$
- $X = \ln x$
- $m = b$
- $c = \ln a$

**How can I use linearised data to find the values of the parameters in an power model y = ax^b?**

STEP 1: Linearise the data using $Y = \ln y$ and $X = \ln x$
STEP 2: Find the equation of the regression line of Y on X : $Y = m X + c$
STEP 3: Equate coefficients between $Y = m X + c$ and $\ln y = \ln a + b \ln x$
- $m = b$
- $c = \ln a$
STEP 4: Solve to find a and b
- $a = e^{c}$
- $b = m$

Worked Example

The graph below shows the heights, $h$ metres, and the amount of time spent sleeping, $t$ hours, of a group of young giraffes. It is believed the data can be modelled using $t = a h^{b}$
.

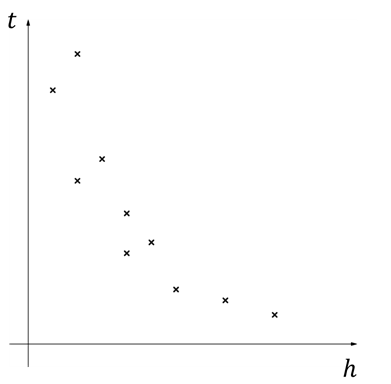
2-7-2-b-we-image

The data are coded using the changes of variables $x = \ln h$ and $y = \ln t$ . The regression line of $y$ on $x$ is found to be $y = 0.3 - 1.2 x$ .

Find the values of $a$ and $b$ .

2-7-2-ib-ai-hl-power-relationships-we-solution

DP IB Maths: AI HL

Revision Notes

4.3.3 Linearising using Logarithms

Exponential Relationships

How do I use logarithms to linearise exponential relationships?

**How can I use linearised data to find the values of the parameters in an exponential model y = ab^x?**

Worked Example

Power Relationships

How do I use logarithms to linearise power relationships?

**How can I use linearised data to find the values of the parameters in an power model y = ax^b?**

Worked Example

Author: Daniel

Resources

Members

Company

Quick Links

DP IB Maths: AI HL

Revision Notes

4.3.3 Linearising using Logarithms

How do I use logarithms to linearise exponential relationships?

How can I use linearised data to find the values of the parameters in an exponential model y = abx?

How do I use logarithms to linearise power relationships?

How can I use linearised data to find the values of the parameters in an power model y = axb?

Author: Daniel

Resources

Members

Company

Quick Links

**How can I use linearised data to find the values of the parameters in an exponential model y = ab^x?**

**How can I use linearised data to find the values of the parameters in an power model y = ax^b?**