Walks & Adjacency Matrices
Adjacency matrices are another way to represent graphs and connections between the different vertices.
What is an adjacency matrix?
- An adjacency matrix is a square matrix where all of the vertices in the graph are listed as the headings for both the rows (
) and columns (
)
- An adjacency matrix can be used to show the number of direct connections between two vertices
- An entry of 0 in the matrix means that there is no direct connection between that pair of vertices
- In a simple graph the only entries are either 0 or 1
- A loop is indicated in an adjacency matrix with a value in the leading diagonal (the line from top left to bottom right)
- In an undirected matrix the value in the leading diagonal will be 2 because you can use the loop to travel out of and into the vertex in two different directions
- In a directed matrix, if the loop has been given a direction, the value in the leading diagonal will be 1 as you can only travel along the loop out of and back into the vertex in one direction
- For a graph with no loops every entry in the leading diagonal will be 0
- An undirected graph will be symmetrical in the leading diagonal
- The sum of the entries in a row is the in degree of that vertex
- The sum of the entries in a column is the out degree of that vertex
Worked Example
Let G be the graph below.
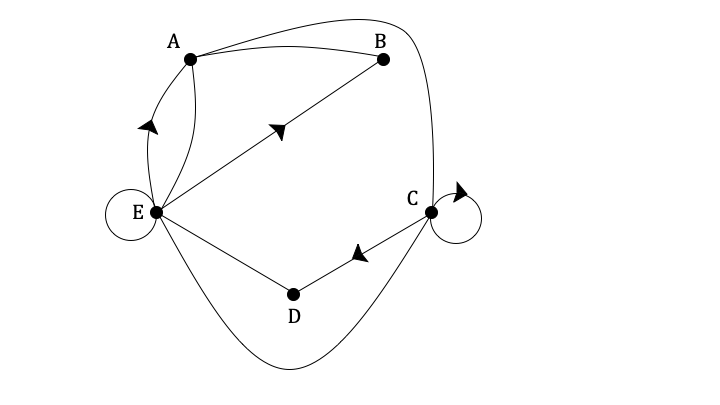
Write down the adjacency matrix for G.

Number of Walks
What is a walk?
- A walk is a sequence of vertices that are visited when moving through a graph along its edges
- Both edges and vertices can be revisited in a walk
- The length of a walk is the total number of edges that are traversed in the walk
How do you find the number of walks in a graph?
- Let M denote the adjacency matrix of a graph. The (i, j) entry in the matrix Mk will give the number of walks of length k from vertex i to vertex j
- If there is an entry of 2 in the leading diagonal of the matrix, this should be changed to a 1 before the matrix is raised to a power
- The number of walks, between vertex i and vertex j, of length n or less can be given by the matrix Sn, where Sn = M1 + M2 +…+…Mn
- If all of the entries in a single row of Sn are non-zero values then the graph is connected
Exam Tip
- Read the question carefully to determine if you need to choose a specific power for the adjacency matrix or if you need to play around with different powers!
Worked Example
The adjacency matrix M of a graph G is given by
a)
Draw the graph described by the adjacency matrix M.

b)
Find the number of walks of length 4 from vertex B to Vertex E.
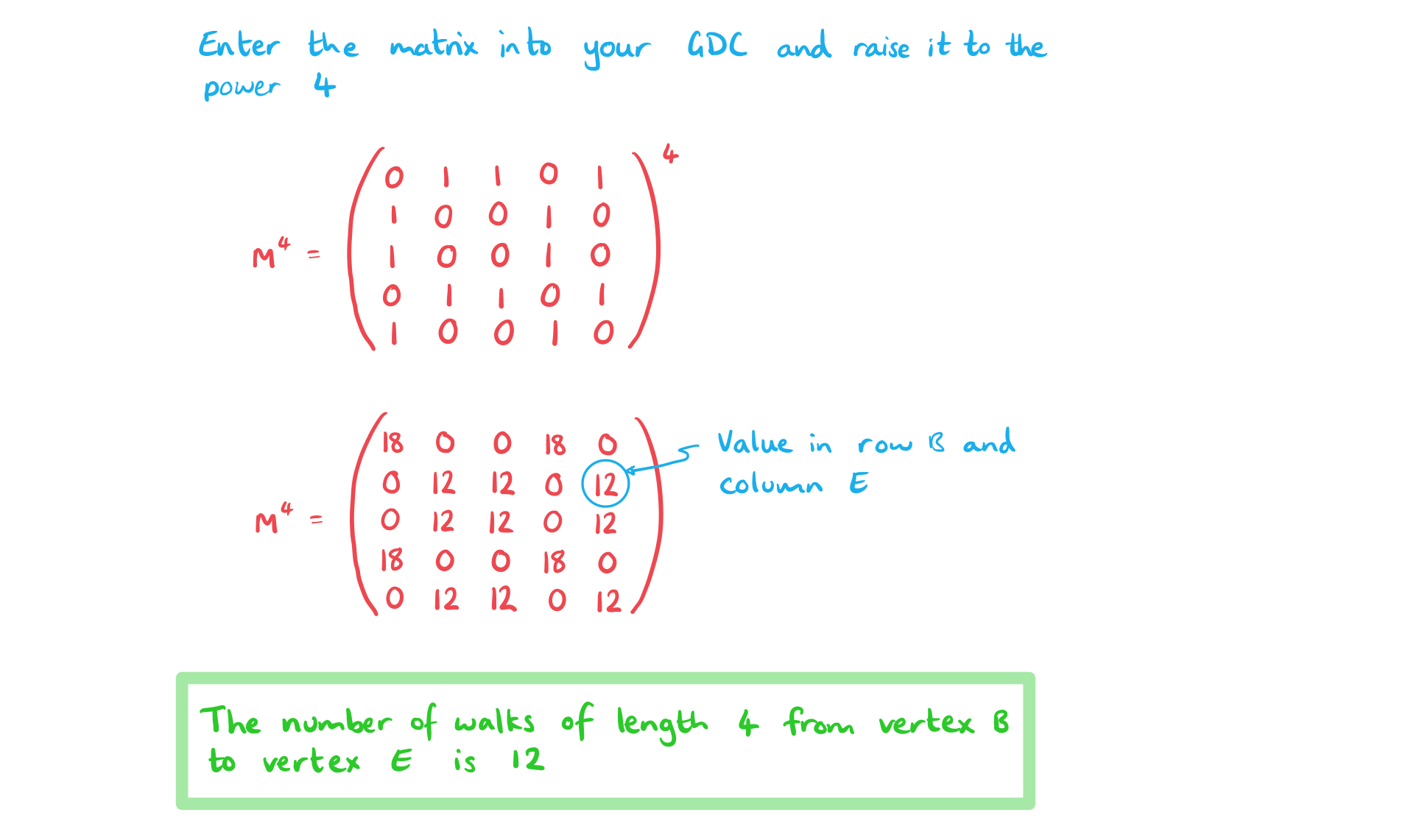
c)
Find the number of walks of 3 or less from vertex A to vertex C.

Weighted Adjacency Tables
A weighted adjacency table gives more detailed information about the connection between different vertices in a weighted graph.
What is a weighted adjacency table?
- A weighted adjacency table is different to an adjacency matrix as the value in each cell is the weight of the edge connecting that pair of vertices
- Weight could be cost, distance, time etc.
- An empty cell can be used to indicate that there is no connection between a pair of vertices
- A directed graph is not symmetrical along the leading diagonal (the line from top left to bottom right)
- When drawing a graph from its adjacency table be careful when labelling the edges
- For an un-directed graph the two cells between a specific pair of vertices will be the same so connect the vertices with one edge labelled with the relevant weight
- For a directed graph if the two cells between a specific pair of vertices have different values draw two lines between the vertices and label each with the correct weight and direction
- A weighted adjacency table can be used to work out the weight of different walks in the graph
Worked Example
The table below shows the time taken in minutes to travel by car between 4 different towns.
| A | B | C | D | |
| A | 16 | 35 | ||
| B | 16 | 20 | 18 | |
| C | 35 | 20 | 34 | |
| D | 23 | 34 |
a)
Draw the graph described by the adjacency table.
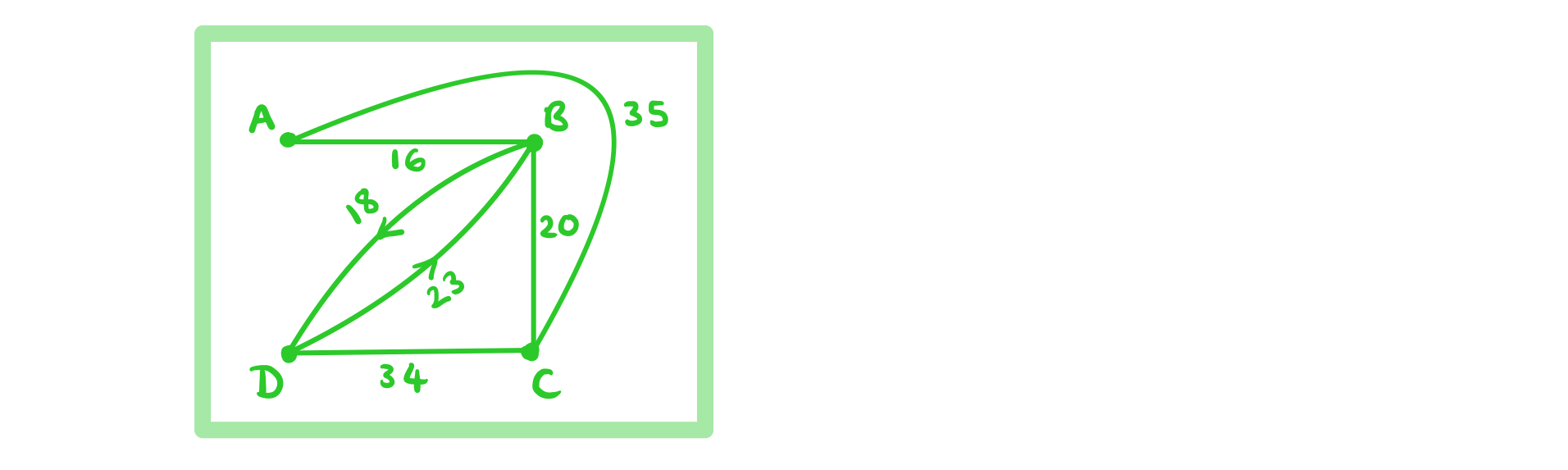
b)
State the time taken to drive from Town B to Town D.

