Solving Systems of Linear Equations with Matrices
Matrices are used in a huge variety of applications within engineering, computing and business. They are particularly useful for encrypting data and forecasting from given data. Using matrices allows for much larger and more complex systems of linear equations to be solved easily.
How do you set up a system of linear equations using matrices?
- A linear equation can be written in the form
, where
is a matrix
- Note that for a system of linear equations to have a unique solution, the matrix must be invertible and therefore must be a square matrix
- In exams, only invertible matrices will be given (except when solving for eigenvectors)
- You should be able to use matrices to solve a system of up to two linear equations both with and without your GDC
- You should be able to use a mixture of matrices and technology to solve a system of up to three linear equations
How do you solve a system of linear equations with matrices?
- STEP 1
Write the information in a matrix equation, e.g. for a system of three linear equations, where the entries into matrix
are the coefficients of
,
and
and matrix
is a column matrix
- STEP 2
Re-write the equation using the inverse of,
- STEP 3
Evaluate the right-hand side to find the values of the unknown variables,
and
Exam Tip
- If you are asked to solve a system of linear equations by hand you can check your work afterwards by solving the same question on your GDC
Worked Example
a)
Write the system of equations
in matrix form.
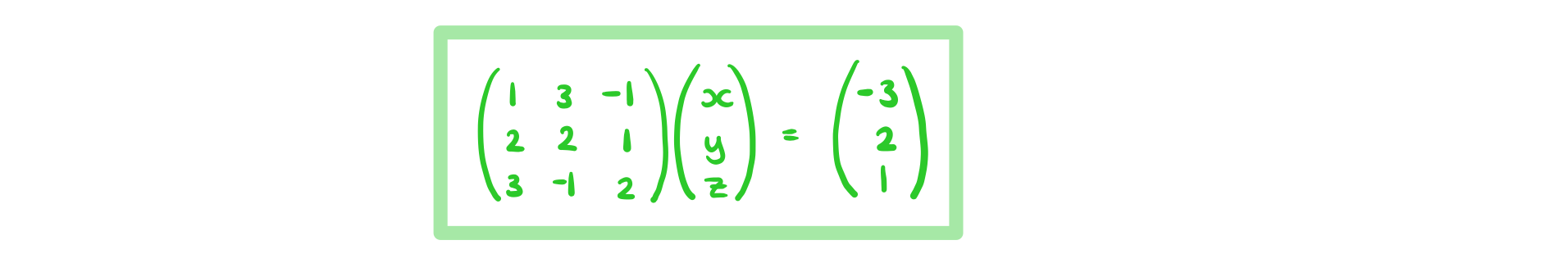
b)
Hence solve the simultaneous linear equations.

