4.9.1 Sample Mean Distribution

Combinations of Normal Variables

What is a linear combination of normal random variables?

Suppose you have n independent normal random variables $X_{i} ~ N (μ_{i}, σ_{i}^{2})$ for i = 1,2,3, ..., n
A linear combination is of the form $X = a_{1} X_{1} + a_{2} X_{2} + \dots + a_{n} X_{n} + b$ where a_i and b are constants
The mean and variance can be calculated using results from random variables
- $E (X) = a_{1} μ_{1} + a_{2} μ_{2} + \dots + a_{n} μ_{n} + b$
- $Var (X) = a_{1}^{2} σ_{1}^{2} + a_{2}^{2} σ_{2}^{2} + \dots + a_{n}^{2} σ_{n}^{2}$
  - The variables need to be independent for this result to be true
A linear combination of n independent normal random variables is also a normal random variable itself
- $X ~ N (a_{1} μ_{1} + a_{2} μ_{2} + \dots + a_{n} μ_{n} + b, a_{1}^{2} σ_{1}^{2} + a_{2}^{2} σ_{2}^{2} + \dots + a_{n}^{2} σ_{n}^{2})$
- This can be used to find probabilities when combining normal random variables

What is meant by the sample mean distribution?

Suppose you have a population with distribution X and you take a random sample with n observations X₁, X₂, ..., X_n
The sample mean distribution is the distribution of the values of the sample mean
- $X = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}$
For an individual sample the sample mean $\bar{x}$ can be calculated
- This is also called a point estimate
- $X$ is the distribution of the point estimates

What does the sample mean distribution look like when X is normally distributed?

If the population is normally distributed then the sample mean distribution is also normally distributed
$E (\bar{X}) = E (\frac{X_{1} + X_{2} + \dots + X_{n}}{n}) = \frac{E (X_{1}) + E (X_{2}) + \dots + {E (X}_{n})}{n} = \frac{μ + μ + \dots + μ}{n} = \frac{n μ}{n} = μ$
$Var (\bar{X}) = Var (\frac{X_{1} + X_{2} + \dots + X_{n}}{n}) = \frac{Var (X_{1}) + Var (X_{2}) + \dots + {Var (X}_{n})}{n ²} = \frac{σ ² + σ ² + \dots + σ ²}{n ²} = \frac{n σ ²}{n ²} = \frac{σ^{2}}{n}$
Therefore you divide the variance of the population by the size of the sample to get the variance of the sample mean distribution
- $X ~ N (μ, σ^{2}) \Rightarrow \bar{X} ~ N (μ, \frac{σ^{2}}{n})$

Worked Example

Amber makes a cup of tea using a hot drink vending machine. When the hot water button is pressed the machine dispenses $W$ ml of hot water and when the milk button is pressed the machine dispenses $M$ ml of milk. It is known that $W ~ N (100, 15^{2})$ and $M ~ N (10, 2^{2})$ .

To make a cup of tea Amber presses the hot water button three times and the milk button twice. The total amount of liquid in Amber’s cup is modelled by $C$ ml.

Write down the distribution of

C

4-9-1-ib-ai-hl-linear-normal-comb-a-we-solution

Find the probability that the total amount of liquid in Amber's cup exceeds 360 ml.

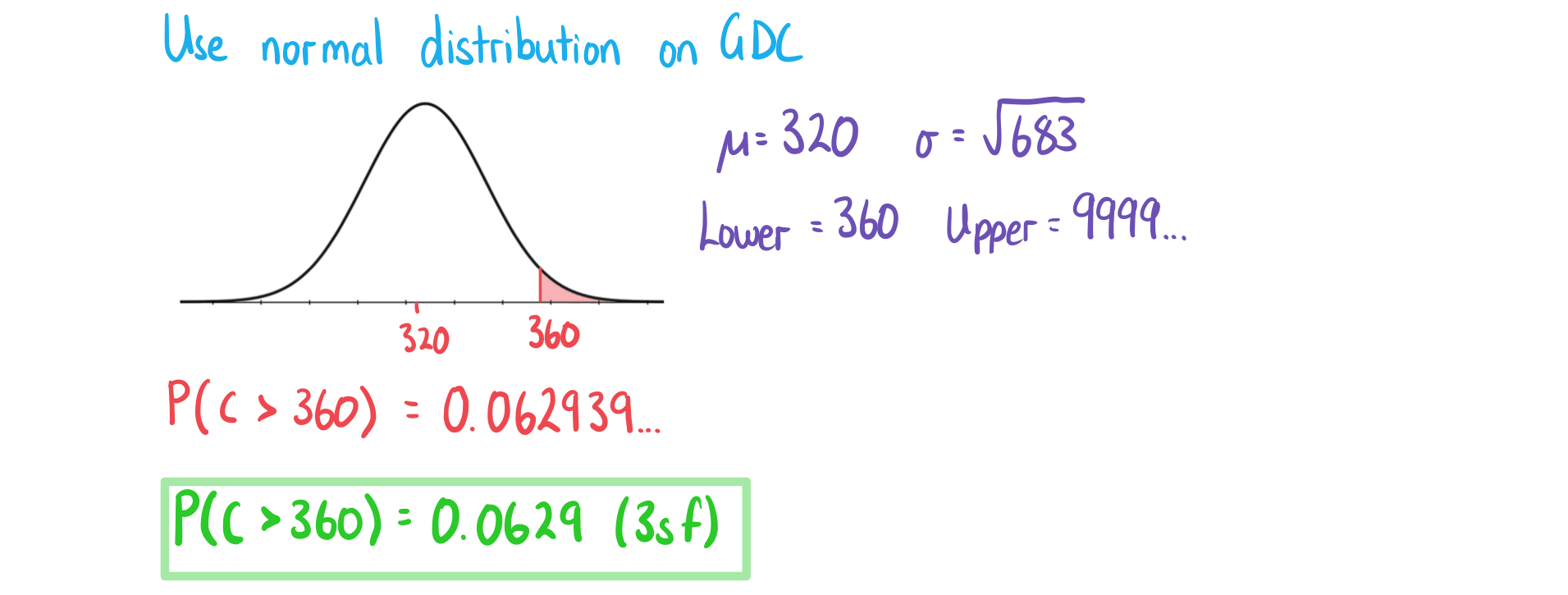
4-9-1-ib-ai-hl-linear-normal-comb-b-we-solution

Amber makes 15 cups of tea and calculates the mean

\bar{C}

. Write down the distribution of

\bar{C}

4-9-1-ib-ai-hl-linear-normal-comb-c-we-solution

Central Limit Theorem

What is the Central Limit Theorem?

The Central Limit Theorem says that if a sufficiently large random sample is taken from any distribution $X$ then the sample mean distribution $\bar{X}$ can be approximated by a normal distribution

In your exam n > 30 will be considered sufficiently large for the sample size

Therefore $\bar{X}$ can be modelled by $N (μ, \frac{σ^{2}}{n})$

μ is the mean of X
σ² is the variance of X
n is the size of the sample

Do I always need to use the Central Limit Theorem when working with the sample mean distribution?

No – the Central Limit Theorem is not needed when the population is normally distributed
If X is normally distributed then $\bar{X}$ is normally distributed

This is true regardless of the size of the sample
The Central Limit Theorem is not needed

If X is not normally distributed then $\bar{X}$ is approximately normally distributed

Provided the sample size is large enough
The Central Limit Theorem is needed

Worked Example

The integers 1 to 29 are written on counters and placed in a bag. The expected value when one is picked at random is 15 and the variance is 70. Susie randomly picks 40 integers, returning the counter after each selection.

Find the probability that the mean of Susie's 40 numbers is less than 13.

4-9-1-ib-ai-hl-central-limit-theorem-a-we-solution

Explain whether it was necessary to use the Central Limit Theorem in your calculation.

4-9-1-ib-ai-hl-central-limit-theorem-b-we-solution

DP IB Maths: AI HL

Revision Notes

4.9.1 Sample Mean Distribution

Combinations of Normal Variables

What is a linear combination of normal random variables?

What is meant by the sample mean distribution?

What does the sample mean distribution look like when X is normally distributed?

Worked Example

Central Limit Theorem

What is the Central Limit Theorem?

Do I always need to use the Central Limit Theorem when working with the sample mean distribution?

Worked Example

Author: Daniel

Resources

Members

Company

Quick Links