5.2.2 Techniques of Differentiation

Chain Rule

What is the chain rule?

The chain rule states if $y$ is a function of $u$ and $u$ is a function of $x$ then

$y = f (u (x))$

$\frac{d y}{d x} = \frac{d y}{d u} \times \frac{d u}{d x}$

- This is given in the formula booklet

In function notation this could be written

$y = f (g (x))$

$\frac{d y}{d x} = f' (g (x)) g' (x)$

How do I know when to use the chain rule?

The chain rule is used when we are trying to differentiate composite functions
- “function of a function”
- these can be identified as the variable (usually $x$ ) does not ‘appear alone’
  - $\sin x$ – not a composite function, $x$ ‘appears alone’
  - $\sin (3 x + 2)$ is a composite function; $x$ is tripled and has 2 added to it before the sine function is applied

How do I use the chain rule?

STEP 1

Identify the two functions

Rewrite

y

as a function of

u

;

y = f (u)

Write

u

as a function of

x

;

u = g (x)

STEP 2

Differentiate

y

with respect to

u

to get

\frac{d y}{d u}

Differentiate

u

with respect to

x

to get

\frac{d u}{d x}

STEP 3

Obtain

\frac{d y}{d x}

by applying the formula

\frac{d y}{d x} = \frac{d y}{d u} \times \frac{d u}{d x}

and substitute

u

back in for

g (x)

In trickier problems chain rule may have to be applied more than once

Are there any standard results for using chain rule?

There are five general results that can be useful
- If $y = {(f (x))}^{n}$ then $\frac{d y}{d x} = n f^{'} (x) f {(x)}^{n - 1}$

- If $y = e^{f (x)}$ then $\frac{d y}{d x} = f^{'} (x) e^{f (x)}$
- If $y = \ln (f (x))$ then $\frac{d y}{d x} = f^{'} (x) \ln (f (x))$
- If $y = \sin (f (x))$ then $\frac{d y}{d x} = f^{'} (x) \cos (f (x))$
- If $y = \cos (f (x))$ then $\frac{d y}{d x} = f^{'} (x) \sin (f (x))$

Exam Tip

You should aim to be able to spot and carry out the chain rule mentally (rather than use substitution)
- every time you use it, say it to yourself in your head
  “differentiate the first function ignoring the second, then multiply by the derivative of the second function"

Worked Example

Find the derivative of

y = {(x^{2} - 5 x + 7)}^{7}

5-2-2-ib-sl-aa-only-chain-we-soltn-a

Find the derivative of

y = \sin (e^{2 x})

5-2-2-ib-sl-aa-only-chain-we-soltn-b

Product Rule

What is the product rule?

The product rule states if $y$ is the product of two functions $u (x)$ and $v (x)$ then

$y = u v$

$\frac{d y}{d x} = u \frac{d v}{d x} + v \frac{d u}{d x}$

- This is given in the formula booklet
In function notation this could be written as

y = f (x) g (x)

\frac{d y}{d x} = {f (x) g}^{'} (x) + {g (x) f}^{'} (x)

‘Dash notation’ may be used as a shorter way of writing the rule

y = u v

y^{'} = u v^{'} + v u'

Final answers should match the notation used throughout the question

How do I know when to use the product rule?

The product rule is used when we are trying to differentiate the product of two functions
- these can easily be confused with composite functions (see chain rule)
  - $\sin (\cos x)$ is a composite function, “sin of cos of $x$ ”
  - $\sin x \cos x$ is a product, “sin x times cos $x$ ”

How do I use the product rule?

Make it clear what $u, v, u'$ and $v'$ are
- arranging them in a square can help
  - opposite diagonals match up

STEP 1

Identify the two functions,

u

and

v

Differentiate both

u

and

v

with respect to

x

to find

u'

and

v'

STEP 2

Obtain

\frac{d y}{d x}

by applying the product rule formula

\frac{d y}{d x} = u \frac{d v}{d x} + v \frac{d u}{d x}

Simplify the answer if straightforward to do so or if the question requires a particular form

In trickier problems chain rule may have to be used when finding $u'$ and $v'$

Exam Tip

Use $u, v, u'$ and $v'$ for the elements of product rule
- lay them out in a 'square' (imagine a 2x2 grid)
- those that are paired together are then on opposite diagonals ( $u$ and $v'$ , $v$ and $u'$ )
For trickier functions chain rule may be reuqired inside product rule
- i.e. chain rule may be needed to differentiate $u$ and $v$

Worked Example

a) Find the derivative of

y = e^{x} \sin x

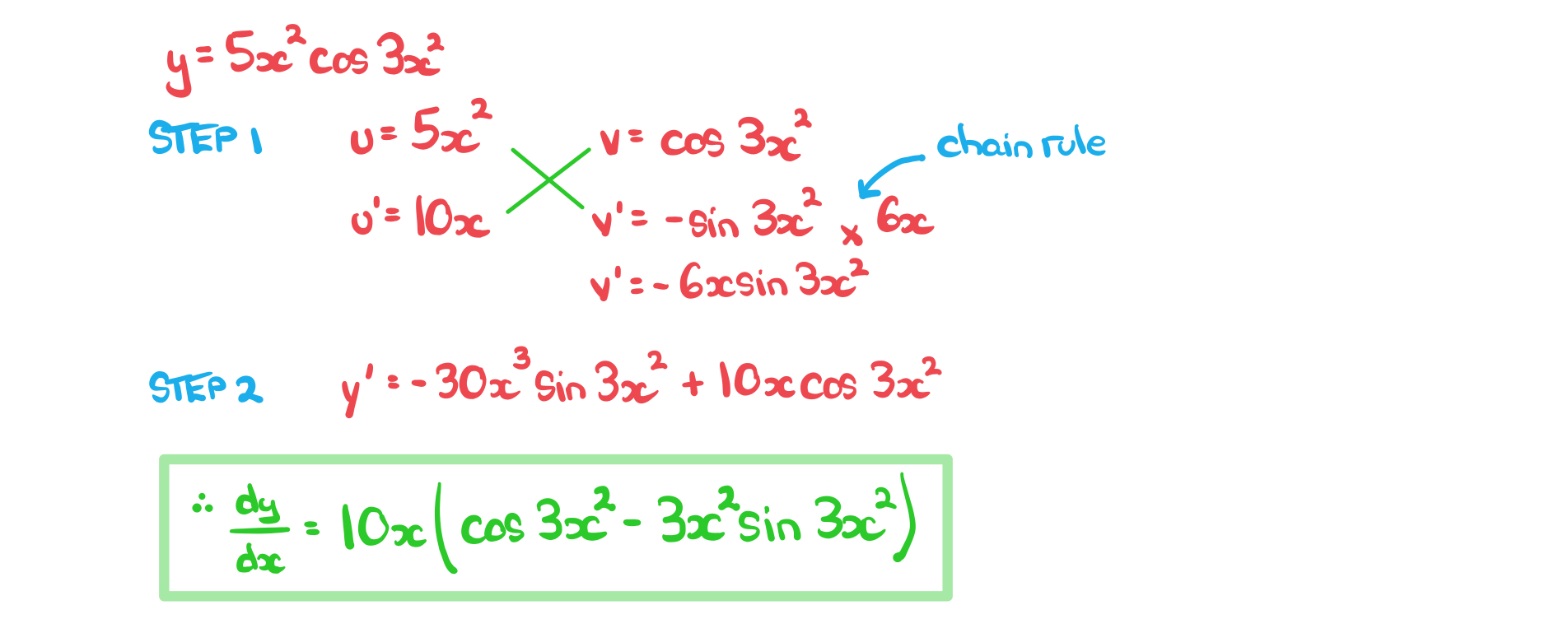
5-2-2-ib-sl-aa-only-product-we-soltn-a

b) Find the derivative of

y = 5 x^{2} \cos 3 x^{2}

5-2-2-ib-sl-aa-only-product-we-soltn-a-b

Quotient Rule

What is the quotient rule?

The quotient rule states if $y$ is the quotient $\frac{u (x)}{v (x)}$ then

$y = \frac{u}{v}$

$\frac{d y}{d x} = \frac{v \frac{d u}{d x} - u \frac{d v}{d x}}{v^{2}}$

- This is given in the formula booklet
In function notation this could be written

y = \frac{f (x)}{g (x)}

\frac{d y}{d x} = \frac{g (x) f^{'} (x) - f (x) g' (x)}{{[g (x)]}^{2}}

As with product rule, ‘dash notation’ may be used

y = \frac{u}{v}

y' = \frac{v u' - u v'}{v^{2}}

Final answers should match the notation used throughout the question

How do I know when to use the quotient rule?

The quotient rule is used when trying to differentiate a fraction where both the numerator and denominator are functions of $x$
- if the numerator is a constant, negative powers can be used
- if the denominator is a constant, treat it as a factor of the expression

How do I use the quotient rule?

Make it clear what $u, v, u'$ and $v'$ are
- arranging them in a square can help
  - opposite diagonals match up (like they do for product rule)

STEP 1

Identify the two functions,

u

and

v

Differentiate both

u

and

v

with respect to

x

to find

u'

and

v'

STEP 2

Obtain

\frac{d y}{d x}

by applying the quotient rule formula

\frac{d y}{d x} = \frac{v \frac{d u}{d x} - u \frac{d v}{d x}}{v^{2}}

Be careful using the formula – because of the minus sign in the numerator, the order of the functions is important

Simplify the answer if straightforward or if the question requires a particular form

In trickier problems chain rule may have to be used when finding $u'$ and $v'$ ,

Exam Tip

Use $u, v, u'$ and $v'$ for the elements of quotient rule
- lay them out in a 'square' (imagine a 2x2 grid)
- those that are paired together are then on opposite diagonals ( $v$ and $u'$ , $u$ and $v'$ )
Look out for functions of the form $y = f (x) (g {(x))}^{- 1}$
- These can be differentiated using a combination of chain rule and product rule
  (it would be good practice to try!)
- ... but it can also be seen as a quotient rule question in disguise
- ... and vice versa!
  - A quotient could be seen as a product by rewriting the denominator as $(g {(x))}^{- 1}$

Worked Example

Differentiate $f (x) = \frac{\cos 2 x}{3 x + 2}$ with respect to $x$ .

DP IB Maths: AI HL

Revision Notes

5.2.2 Techniques of Differentiation

Chain Rule

What is the chain rule?

How do I know when to use the chain rule?

How do I use the chain rule?

Are there any standard results for using chain rule?

Exam Tip

Worked Example

Product Rule

What is the product rule?

How do I know when to use the product rule?

How do I use the product rule?

Exam Tip

Worked Example

Quotient Rule

What is the quotient rule?

How do I know when to use the quotient rule?

How do I use the quotient rule?

Exam Tip

Worked Example

Author: Lucy

Resources

Members

Company

Quick Links