Markov Chains
What is meant by a “state”?
- States refer to mutually exclusive events with the current event able to change over time
- Examples of states include:
- Daily weather conditions
- The states could be: “sunny” and “not sunny”
- Countries visited by an inspector each day
- The states could be: “France”, “Spain” and “Germany”
- Store chosen for weekly grocery shop:
- The states could be: “Foods-U-Like”, “Smiley Shoppers” and “Better Buys”
What is a Markov chain?
- A Markov chain is a model that describes a sequence of states over a period of time
- Time is measured in discrete steps
- Such as days, months, years, etc
- The conditions for a Markov chain are:
- The probability of a state being the next state in the sequence only depends on the current state
- For example
The 11th state only depends on the 10th state
The first 9 states do not affect the 11th state - This probability is called a transition probability
- The transition probabilities do not change over time
- For example
The probability that the 11th state is A given that the 10th state is B is equal to the probability that the 12th state is A given that the 11th state is B - A Markov chain is said to be regular if it possible to reach any state after a finite period of time regardless of the initial state
What is a transition state diagram?
- A transition diagram is a directed graph
- The vertices are the states
- The edges represent the transition probabilities between the states
- The graph can contain
- Loops
- These will be the transition probabilities of the next state being the same as the current state
- Two edges between each pair of vertices
- The edges will be in opposite directions
- Each edge will show the transition probability of the state changing in the given direction
- The probabilities on the edges coming out of a vertex add up to 1
Exam Tip
- Drawing a transition state diagram (even when the question does not ask for one) can help you visualise the problem
Worked Example
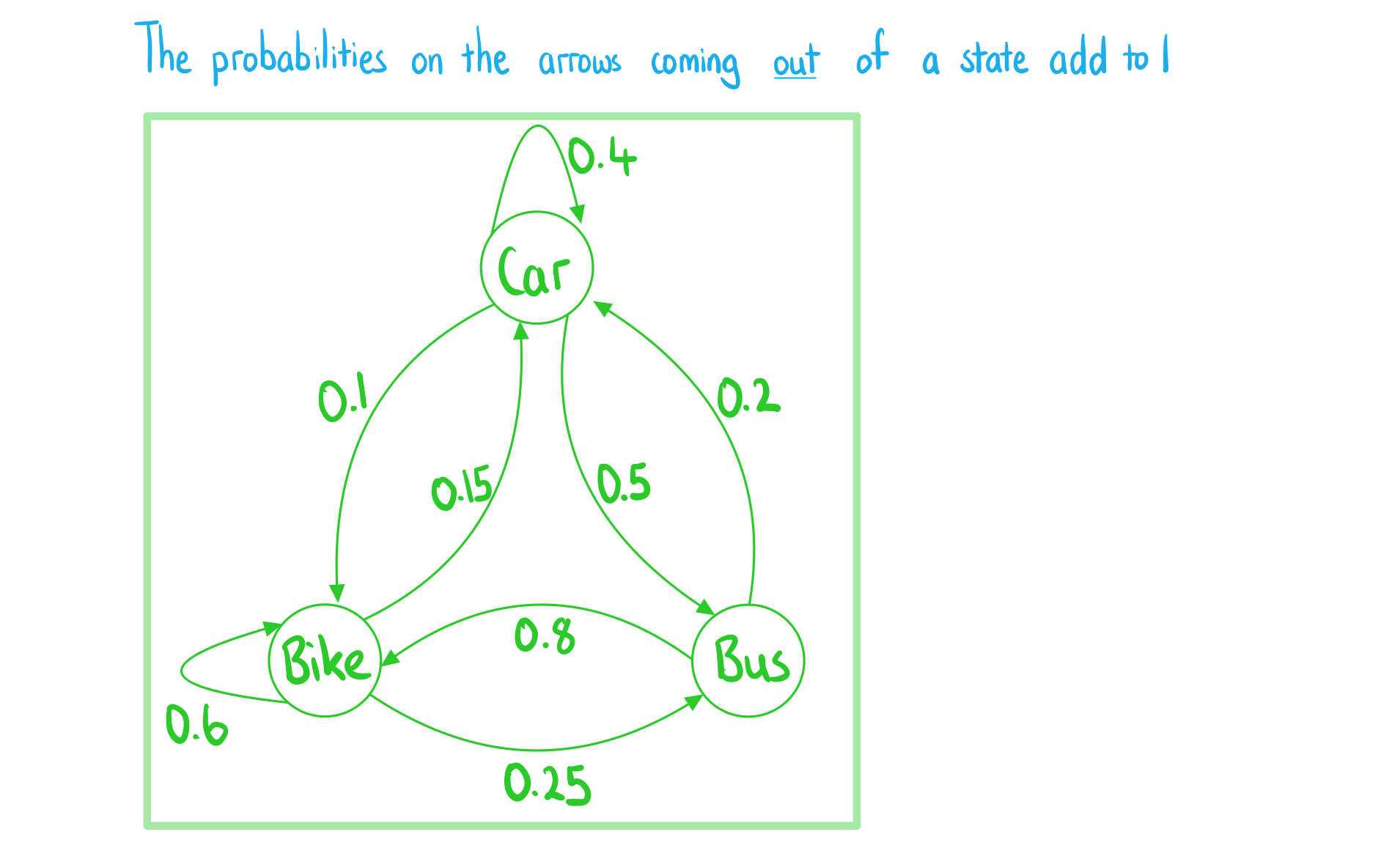
Fleur travels to work by car, bike or bus. Each day she chooses her mode of transport based on the transport she chose the previous day.
- If Fleur travels by car then there is a 40% chance that she will travel by car the following day and a 10% chance that she will travel by bike.
- If Fleur travels by bike then there is a 60% chance that she will travel by bike the following day and a 25% chance that she will travel by bus.
- If Fleur travels by bus then there is an 80% chance that she will travel by bike the following day and a 20% chance that she will travel by car.
Represent this information as a transition state diagram.