Hamiltonian Paths & Cycles
What are Hamiltonian paths and cycles?
- A path is a walk in which no vertices are repeated
- A Hamiltonian path is a path in which each vertex in a graph is visited exactly once
- A cycle is a walk that starts and ends at the same vertex and repeats no other vertices
- A Hamiltonian cycle is a cycle which visits each vertex in a graph exactly once
- If a graph contains a Hamiltonian cycle then it is known as a Hamiltonian graph
- A graph is semi-Hamiltonian if it contains a Hamiltonian path but not a Hamiltonian cycle
- The only way to show that a graph is Hamiltonian or semi-Hamiltonian is to find a Hamiltonian cycle or Hamiltonian trail
Exam Tip
- If you are given an adjacency matrix and are asked to find a Hamiltonian cycle, make sure that you sketch out the graph first
Worked Example
Let G be the graph shown below.
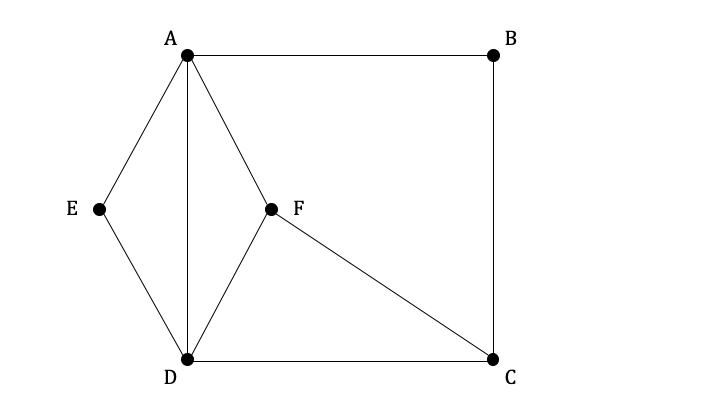
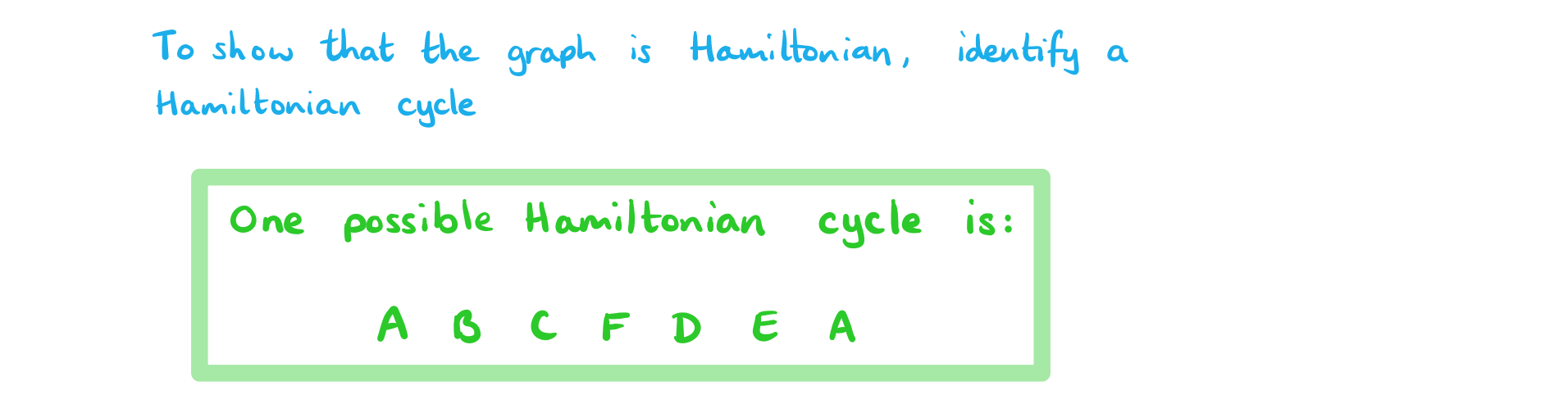
Show that G is a Hamiltonian graph.
Travelling Salesman Problem
The travelling salesman problem requires you to find the route of least weight that starts and finishes at the same vertex and visits every other vertex in the graph exactly once.
How do I solve the travelling salesman problem?
- In the classical travelling salesman problem the following conditions are observed:
- the graph is complete
- the direct route between two vertices is the shortest route (it satisfies the triangle inequality)
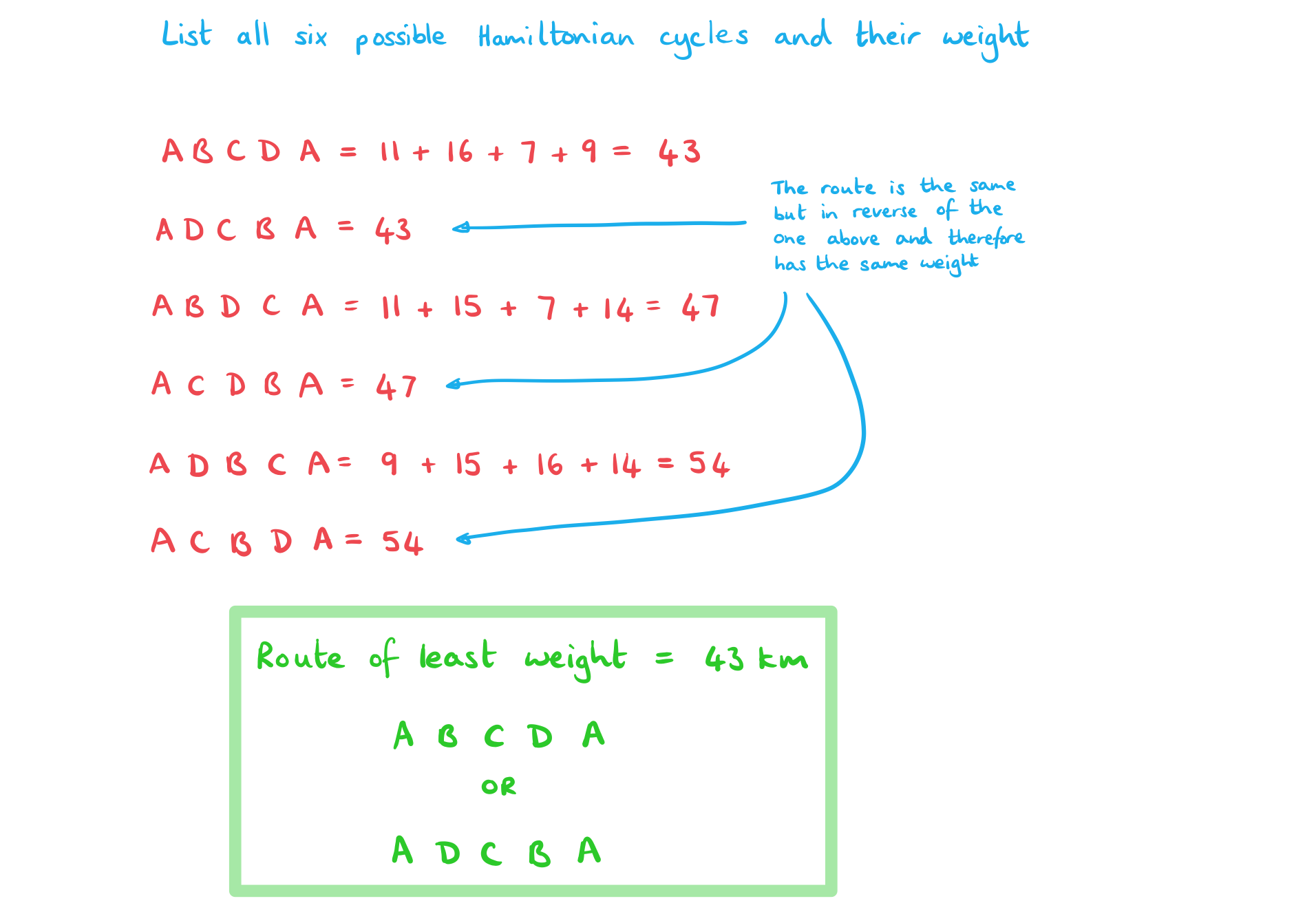
- List all of the possible Hamiltonian cycles and find the cycle of least weight
- A complete graph with 3 vertices will have 2 possible Hamiltonian cycles, 4 vertices will have 6 possible cycles and a graph with 5 vertices will have 24 possible cycles
- There is no known algorithm that guarantees finding the shortest Hamiltonian cycle in a graph so this method is only suitable for small graphs
Exam Tip
- To remember the difference between the travelling salesman problem and the Chinese postman problem, remember that the salesman is interested in selling at each destination (vertex) whereas the postman wants to walk along every road (edge) in order to deliver the letters
Worked Example
The graph below shows four towns and the distances between them in km.
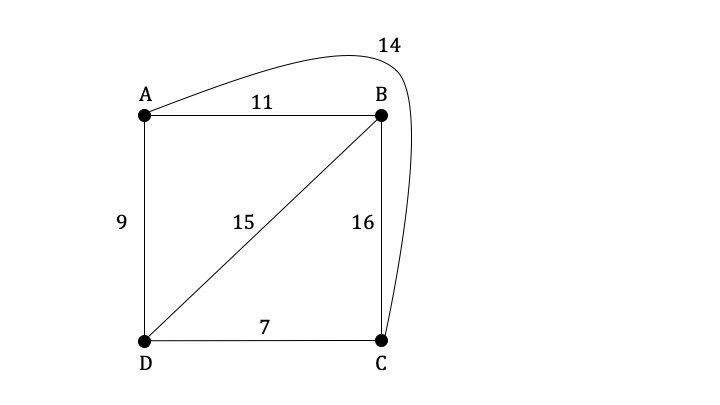
A salesman lives in city A and wishes to travel to each of the other three cities before returning home.
Find the shortest route that the salesman could take and state the total length of the route.