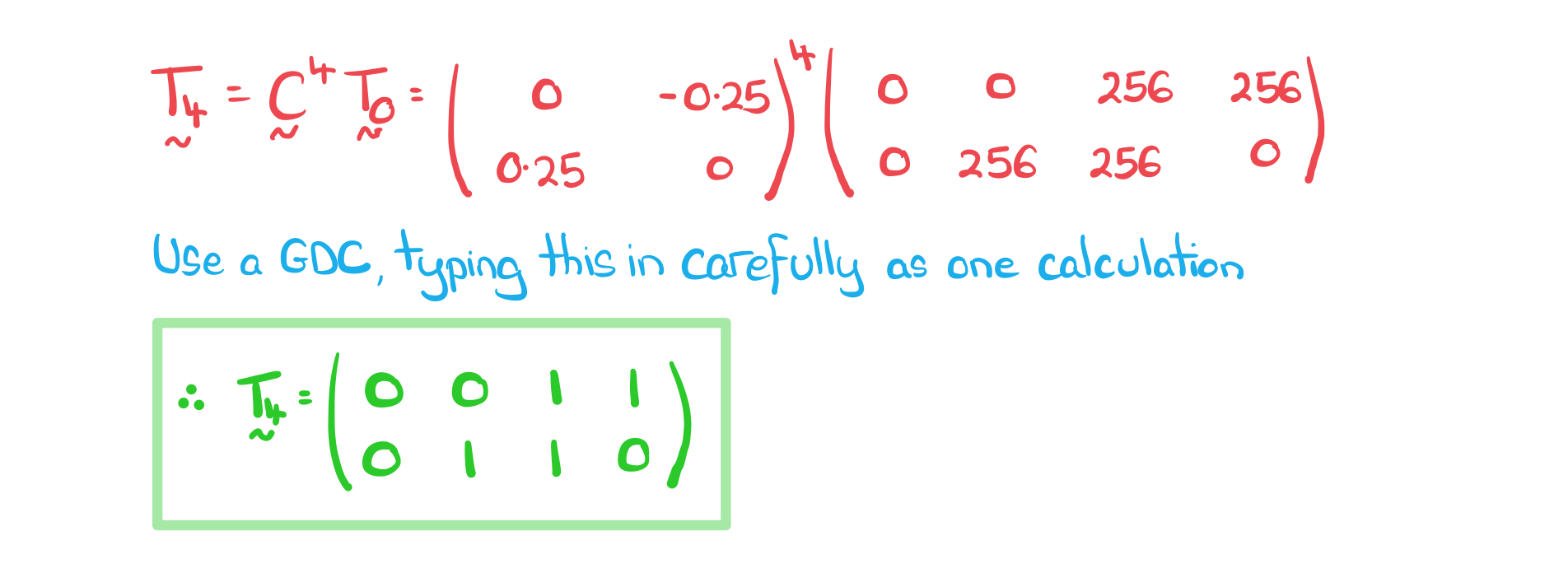3.6.1 Matrix Transformations

What is a transformation matrix?

• A transformation matrix is used to determine the coordinates of an image from the transformation of an object
• Commonly used transformation matrices include
• reflections, rotations, enlargements and stretches
• (In 2D) a multiplication by any 2x2 matrix could be considered a transformation (in the 2D plane)
• An individual point in the plane can be represented as a position vector, 
• Several points, that create a shape say, can be written as a position matrix 
• A matrix transformation will be of the form 
• where  represents any point in the 2D plane
•   and  are given matrices

How do I find the coordinates of an image under a transformation?

• The coordinates (x’, y’) - the image of the point (x, y) under the transformation with matrices  and - are given by

• Similarly, for a position matrix

• • If you use this method then remember to add e and f to each column
• A GDC can be used for matrix multiplication
  • If matrices involved are small, it may be as quick to do this manually 

• STEP 1
  Determine the transformation matrix (T) and the position matrix (P)
  The transformation matrix, if uncommon, will be given in the question
  The position matrix is determined from the coordinates involved, it is best to have the coordinates in order, to avoid confusion 

• STEP 2
  Set up and perform the matrix multiplication and addition required to determine the image position matrix, P’
  P’ = TP 

• STEP 3
  Determine the coordinates of the image from the image position matrix, P’

How do I find the coordinates of the original point given the image under a transformation?

•  To ‘reverse’ a transformation we would need the inverse transformation matrix
  • i.e. T^-1
  • For a 2x2 matrix the inverse is given by 
    • where 
  • A GDC can be used to work out inverse matrices
• You would rearrange 
  • 

What is meant by a geometric transformation?

• The following transformations can be represented (in 2D) using multiplication of a 2x2 matrix
• rotations (about the origin)
• reflections
• enlargements
• (horizontal) stretches parallel to the x-axis
• (vertical) stretches parallel to the y-axis
• The following transformations can be represented (in 2D) using addition of a 2x1 matrix
• translations

What are the matrices for geometric transformations?

• All of the following transformation matrices are given in the formula booklet
• Rotation
  • Anticlockwise (or counter-clockwise) through angle θ about the origin
    • 
  • Clockwise through angle θ about the origin
    • 
  • In both cases
    • θ > 0
    • θ may be measured in degrees or radians
• Reflection
  • In the line 
    • 
  • θ may be measured in degrees or radians
  • for a reflection in the x-axis, θ = 0° (0 radians)
  • for a reflection in the y-axis, θ = 90° (π/2 radians)
• Enlargement
  • Scale factor k, centre of enlargement at the origin (0, 0)
    • 
• Horizontal stretch (or stretch parallel to the x-axis)
  • Scale factor k
    • 
• Vertical stretch (or stretch parallel to the y-axis)
  • Scale factor k
    • 
• Translation (vector)
  • p units in the (positive) x-direction
  • q units in the (positive) y direction
    • 
    • This is not given in the formula booklet

How do I solve problems involving geometric transformations?

• The matrix equations involved in problems will be of the form
  • P’=AP or
  • P’=AP+b where b is a translation vector
    • (sometimes called an affine transformation)
  • where
    • P is the position vector of the object coordinates
    • P’ is the position vector of the image coordinates
    • A is the transformation matrix
    • b is a translation vector
• Problems may ask you to
  • find the coordinates of point(s) on the image
  • find the coordinates of point(s) on the object using an inverse matrix (A^-1)
  • deduce/identify a matrix corresponding to one of the common geometric transformations
    • E.g. Find the matrix of a rotation of 45° clockwise about the origin

The order in which transformations occur can lead to different results – for example a reflection in the x-axis followed by clockwise rotation of 90°  is different to rotation first, followed by the reflection.

Therefore, when one transformation is followed by another order is critical.

What is a composite transformation?

• A composite function is the result of applying more than one function to a point or set of points
• e.g.  a rotation, followed by an enlargement
• It is possible to find a single composite function matrix that does the same job as applying the individual transformation matrices

How do I find a single matrix representing a composite transformation?

• Multiplication of the transformation matrices
• However, the order in which the matrices is important
  • If the transformation represented by matrix M is applied first, and is then followed by another transformation represented by matrix N
    • the composite matrix is NM
      e. P’ = NMP
      (NM is not necessarily equal to MN)
    • The matrices are applied right to left
    • The composite function matrix is calculated left to right
  • Another way to remember this is, starting from P, always pre-multiply by a transformation matrix
    • This is the same as applying composite functions to a value
    • The function (or matrix) furthest to the right is applied first

How do I apply the same transformation matrix more than once?

• If a transformation, represented by the matrix T, is applied twice we would write the composite transformation matrix as T²
  • T² = TT
• This would be the case for any number of repeated applications
  • T⁵ would be the matrix for five applications of a transformation
• A GDC can quickly calculate T², T⁵, etc
• Problems may involve considering patterns and sequences formed by repeated applications of a transformation
  • The coordinates of point(s) follow a particular pattern
    • (20, 16) – (10, 8) – (5, 4) – (2.5, 2) …
  • The area of a shape increases/decreases by a constant factor with each application

e.g. if one transformation doubles the area then three applications will increase the (original) area eight times (2³)