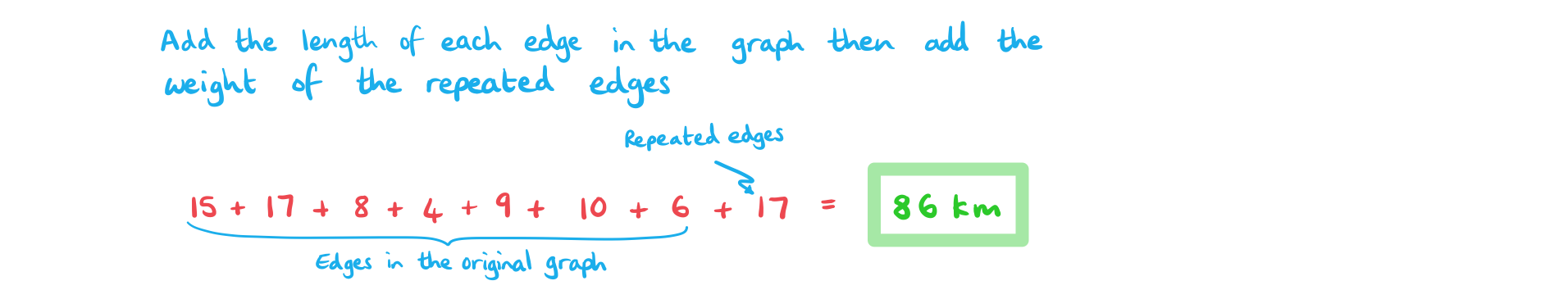Eulerian Trails & Circuits
What are Eulerian trails and circuits?
- A trail is a walk in which no edge is repeated
- An Eulerian trail is a trail that visits each edge in a graph exactly once
- A circuit is a trail that begins and ends at the same vertex
- An Eulerian circuit is a trail that visits each edge in a graph exactly once and begins and ends at the same vertex
- A graph which contains an Eulerian circuit is called an Eulerian graph
- In an Eulerian graph the degree of each vertex is even
- A semi-Eulerian graph contains an Eulerian trail but not an Eulerian circuit
- In a semi-Eulerian graph exactly one pair of vertices have an odd degree
- These are the start and finish points of any Eulerian trail
- An adjacency matrix can be used to determine if a graph is Eulerian or semi-Eulerian as the degree of each vertex can be found by inspecting the sum of the entries in the rows (out-degree) or columns (in-degree)
Exam Tip
- If you can draw a graph without taking your pen off the paper and without going over any edge more than once then you have an Eulerian or semi-Eulerian graph!
Worked Example
Let G be the graph shown below.
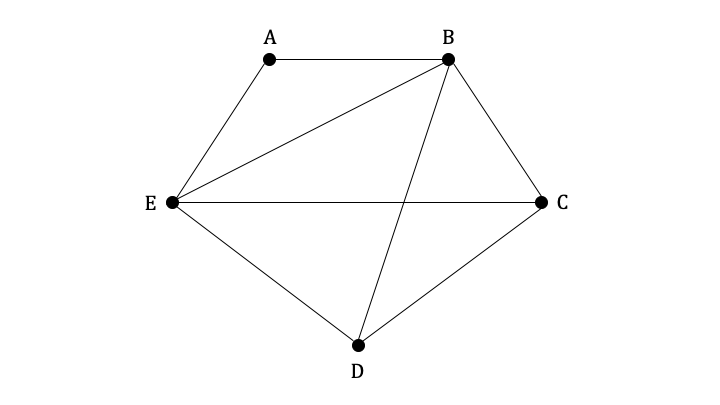
a)
Show that G is a semi-Eulerian graph.

b)
Write down an Eulerian trail for G.

Chinese Postman Problem
The Chinese postman problem requires you to find the route of least weight that starts and finishes at the same vertex and traverses every edge in the graph. Some edges may need to be traversed twice and the challenge is to minimise the total weight of these repeated edges.
How do I solve the Chinese postman problem?
- If all of the vertices in a graph are even then the shortest route will be the sum of the weights of the edges in an Eulerian circuit
- If there is one pair of odd vertices in the graph then the shortest route between them will need to be found and repeated before finding an Eulerian circuit
- There will always be an even number of odd vertices as the total sum of the degrees of the vertices is double the number of edges
- If there are more than two odd vertices, then each possible pairing of the odd vertices must be considered in order to find the minimum weight of the edges that need to be repeated
- The maximum number of odd vertices that could appear in an exam question is 4
What are the steps of the Chinese postman algorithm?
- STEP 1
Inspect the degree of all of the vertices and identify any odd vertices - STEP 2
Find the possible pairings between the odd vertices - STEP 3
For each possible combination of vertices, find the shortest walk between the vertices and add the edges to be repeated to the graph - STEP 4
Write down an Eulerian circuit of the adjusted graph to find a possible route and find the sum of the edges traversed to find the total weight
What variations may there be on the Chinese postman algorithm?
- The weighting of the edge between a pair of vertices may be different depending on if it is the first time it is being traversed or a repeat.
- For example, if an inspector was checking a pipeline for defects then the first time going along a section of pipeline could take longer during inspection than if it is being repeated in order to get from one vertex to another
- If there are 4 odd vertices you may be asked to start and finish at different vertices. Find the length of the routes for all possible pairings of the odd vertices and choose the shortest route between any 2 of them to be repeated. The other two odd vertices will be your start and finish points.
Exam Tip
- Look carefully for the shortest route between two vertices exam questions often have graphs where a combination of edges will turn out to be a shorter distance than a more direct route
Worked Example
The graph G shown below displays the distances, in kilometres, of the main roads between towns A, B, C, D and E. Each road is to be inspected for potholes.
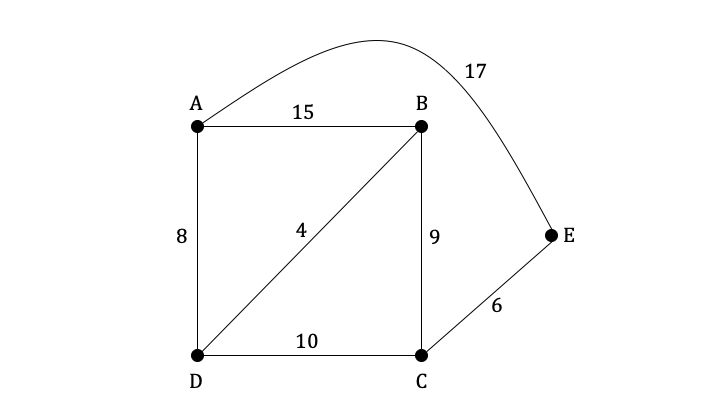
a)
Explain why G does not contain an Eulerian circuit.

b)
Find the shortest route that starts and finishes at town A and allows for each road to be inspected.

c)
State the total length of the shortest route.