4.3.1 Non-linear Regression

Non-linear Regression

What is non-linear regression?

You have already seen that linear regression is when you can use a straight line to fit bivariate data
Non-linear regression is when you can use a curve (rather than a straight line) to fit bivariate data
In your exam the regression could be:

Linear: $y = a x + b$
Quadratic: $y = a x^{2} + b x + c$
Cubic: $y = a x^{3} + b x^{2} + c x + d$
Exponential: $y = a b^{x}$ or $y = a e^{b x}$
Power: $y = a x^{b}$
Sine: $y = a \sin (b x + c) + d$

How do I find the equation of the non-linear regression model?

Using your GDC:
- Type the two sets of the data into your GDC
- Select the relevant model
  - The exam question will tell you which model to use
- Your GDC will calculate the constants
You can use logarithms to linearise exponential and power relationships
- Power: $y = a x^{b}$ then $\ln y = \ln a + b \ln x$
  - $\ln y$ and $\ln x$ will have a linear relationship
- Exponential: $y = a b^{x}$ then $\ln y = \ln a + x \ln b$
  - $\ln y$ and $x$ will have a linear relationship

Exam Tip

You can use your GDC to plot the scatter diagram and include the graph of a regression model
- This will allow you to get a sense of how well the model fits the data

Worked Example

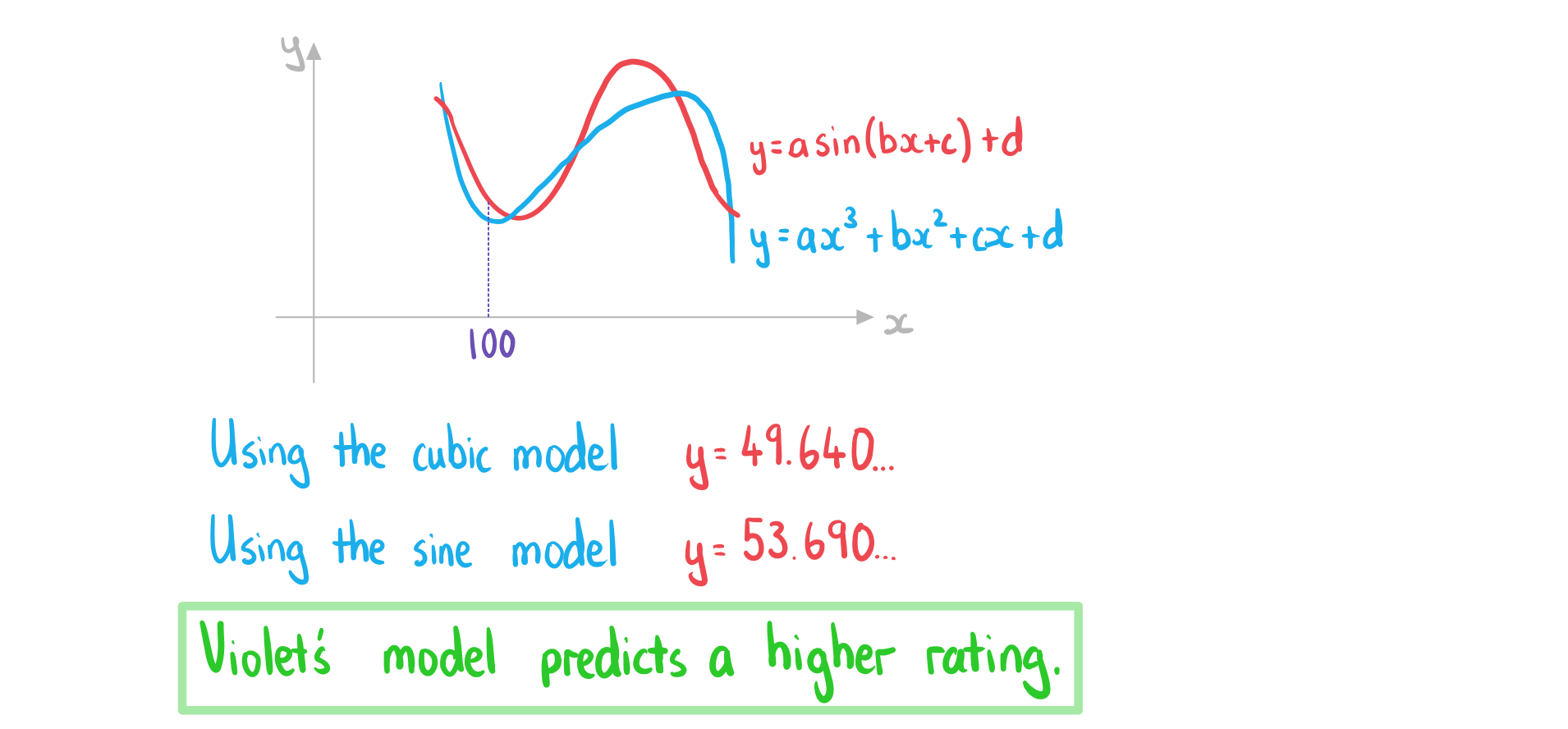
Scarlett and Violet collect data on the length of a film ( $x$ minutes) and the audience rating ( $y$ %).

$x$	75	93	101	107	115	124	132	140	171
$y$	83	75	51	38	47	56	76	91	70

Scarlett claims that there is a cubic relationship. Find the equation of a cubic regression model of the form

y = a x^{3} + b x^{2} + c x + d

4-3-1-ib-ai-hl-non-linear-regression-a-we-solution

Violet claims that there is a sine relationship. Find the equation of a sine regression model of the form

y = a \sin (b x + c) + d

4-3-1-ib-ai-hl-non-linear-regression-b-we-solution

Whose model predicts a higher audience rating for a film which is 100 minutes long?

4-3-1-ib-ai-hl-non-linear-regression-c-we-solution

Least Squares Regression Curves

What is a residual?

Given a set of n pairs of data and a regression model y = f(x)
A residual is the actual y-value (from the data) minus the predicted y-value (using the regression model)
- $y_{i} - f (x_{i})$
The sum of the square residuals is denoted by $S S_{r e s}$
- $S S_{r e s} = \sum_{i = 1}^{n} {(y_{i} - f (x_{i}))}^{2}$
If you have two regression models using the same data then the one with the smaller $S S_{r e s}$ fits the data better

What is a least squares regression curve?

The least squares regression curve can be thought of as a “curve of best fit” y = f(x)
For a given type of model the least squares regression curve minimises the sum of the square residuals

Your GDC calculates the constants for the least squares regression curves

Why is the sum of the square residuals not always a good measure of fit?

If two models are formed using the same number of pairs of data then the sum of the square residuals is a good measure of fit
If two models use different number of pairs of data then $S S_{r e s}$ is not always a good measure of fit
- The sum will increase with more pairs of data and so can no longer be compared against a data set with a different number of pairs
- Compare the two scenarios
  - 10 pairs of data and the absolute value of each residual is 15 then $S S_{r e s} = 10 \times 15^{2} = 2250$
  - 2250 pairs of data and the absolute value of each residual is 1 then $S S_{r e s} = 2250 \times 1^{2} = 2250$
- They have the same value of $S S_{r e s}$ but the residuals in the second scenario are much smaller
Your GDC may give you the mean squared error
- $M S e = \frac{1}{n} S S_{r e s} = \frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - f (x_{i}))}^{2}$
- This is a better measure of fit
- You do not need to know this for your exam but it might help with your understanding

Worked Example

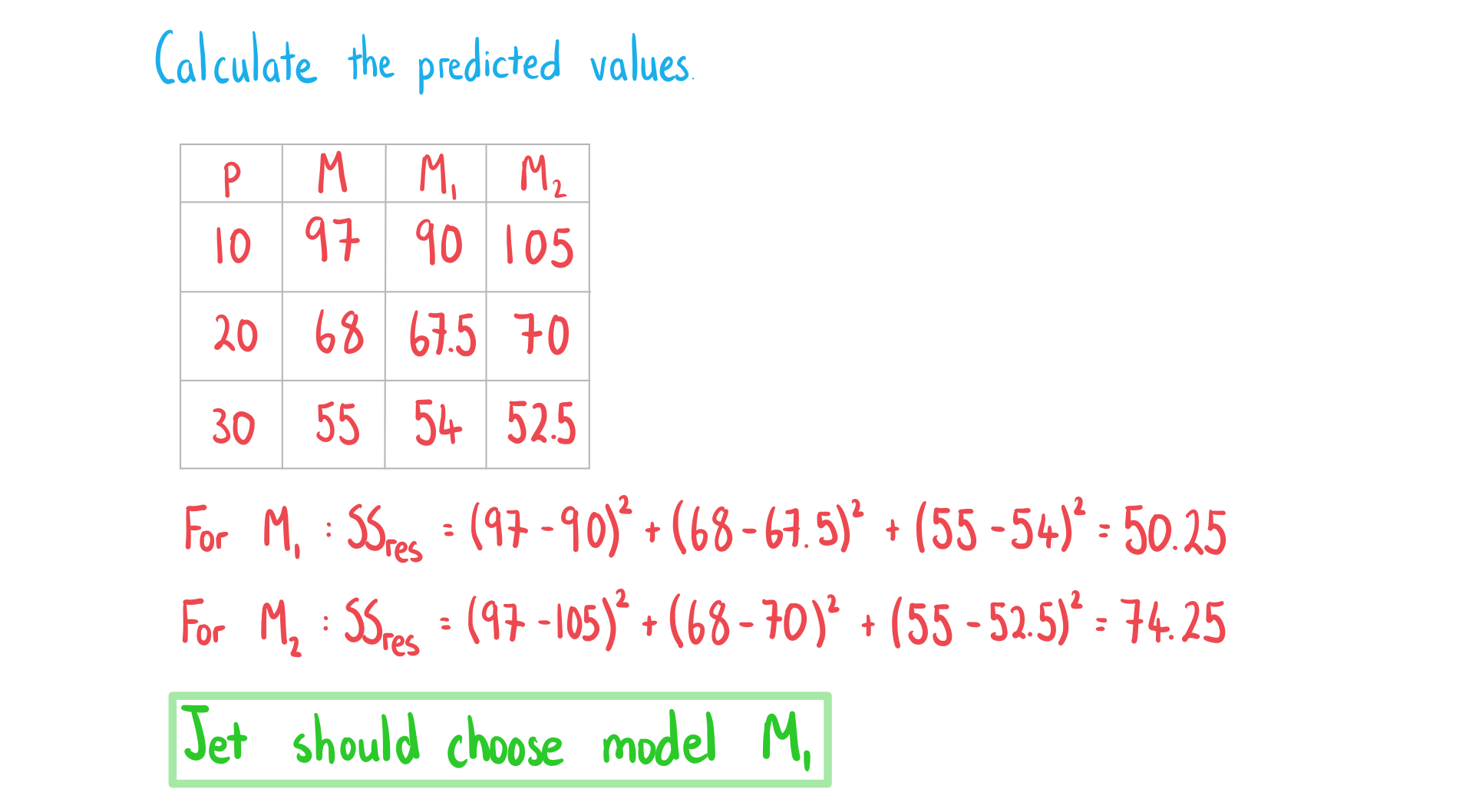
Jet is the owner of a gym and he is testing different prices options. The table below shows the number of new members per month ( $M$ ) and the price of a monthly membership ( $£ p$ ).

$p$	10	20	30
$M$	97	68	55

Jet believes that he can fit the data with either the model $M_{1} (p) = \frac{2700}{p + 20}$ or the model $M_{2} (p) = \frac{2100}{p + 10}$ .

Jet wants to choose the model with the smallest value for the sum of square residuals.

Determine which model Jet should choose.

4-3-1-ib-ai-hl-least-squares-regression-we-solution

The Coefficient of Determination

What is the coefficient of determination?

The coefficient of determination is a measure of fit for a model
- If the coefficient of determination is 0.57 this means 57% of the variation of the y-variable can be explained by the variation in the x-variable
- The other 43% can be explained by other factors
- The higher this proportion the more the model fits the data
The coefficient of determination is denoted by R²
- R² ≤ 1
- R² = 1 means the model is a perfect fit for the data
- The closer to 1 the better the fit
- R² is usually greater than or equal to zero
  - R² can be negative but this is outside the scope of this course
If the regression model is linear then the coefficient of determination is equal to square of the PMCC
- $R^{2} = r^{2}$ for linear models
- Some GDCs will simply denote R² as r² due to its connection to the PMCC for linear models

How do I calculate the coefficient of determination?

When finding the constants for regression models your GDC might give you the value of $R^{2}$
- You will only be asked to calculate the coefficient of determination for models for which GDCs give the value of R²
The coefficient of determination can be calculated by
- $R^{2} = 1 - \frac{S S_{r e s}}{S S_{t o t}}$
  - Where $S S_{t o t} = \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}$
- You do not need to know this formula but it might help with your understanding

Does the coefficient of determination determine the validity of a model?

If R² is close to 1 then the model fits the data well

However this alone does not guarantee that it is a good model for the relationship between the two variables

Consider the scenario where there are big gaps between data points and a model which fits the data well

The model only fits the data at the data points
As there are gaps between the data points the model might not be a good fit for these areas

Different types of models have different number of parameters

Therefore using different types of models to fit the same data will have different levels of accuracy
Linear models need at least two pairs of data
Quadratic models need at least three pairs of data
Cubic models need at least four pairs of data

Using four pairs of data will mean the cubic model will have R² = 1
This is because the cubic graph will go through all four pieces of data – the value is likely to decrease as extra pairs of data are included
However this does not mean it is a better fit than the quadratic model
The quadratic model could be more accurate as it has one more pair of data than is needed

Worked Example

Data is collected on the lengths of cheetahs ( $x$ metres) and their average running speeds ( $y$ ms^-1).

$x$	1.21	1.33	1.12	1.45	1.42	1.39	1.24	1.19	1.32
$y$	24.3	25.1	22.2	35.1	35.1	33.4	27.1	23.1	24.8

Find the equation of the least squares regression curve using:

(i)

a quadratic model

y = a x^{2} + b x + c

(ii)

an exponential model

y = a b^{x}

4-3-1-ib-ai-hl-coefficient-determination-a-we-solution

Based solely on the coefficients of determination, suggest which model is better fit for the data.

4-3-1-ib-ai-hl-coefficient-determination-b-we-solution

DP IB Maths: AI HL

Revision Notes

4.3.1 Non-linear Regression

Non-linear Regression

What is non-linear regression?

How do I find the equation of the non-linear regression model?

Exam Tip

Worked Example

Least Squares Regression Curves

What is a residual?

What is a least squares regression curve?

Why is the sum of the square residuals not always a good measure of fit?

Worked Example

The Coefficient of Determination

What is the coefficient of determination?

How do I calculate the coefficient of determination?

Does the coefficient of determination determine the validity of a model?

Worked Example

Author: Daniel

Resources

Members

Company

Quick Links