Components of Vectors
Why do we write vectors in component form?
- When working with vectors in context it is often useful to break them down into components acting in a direction that is not one of the base vectors
- The base vectors are vectors acting in the directions i, j and k
- The vector will need to be resolved into components that are acting perpendicular to each other
- Usually, one component will be acting parallel to the direction of another vector and the other will act perpendicular to the direction of the vector
- For example: the components of a force parallel and perpendicular to the line of motion allows different types of problems to be solved
- The parallel component of a force acting directly on a particle will be the component that causes an effect on the particle
- The perpendicular component of a force acting directly on a particle will be the component that has no effect on the particle
- The two components of the force will have the same combined effect as the original vector
How do we write vectors in component form?
- Use trigonometry to resolve a vector acting at an angle
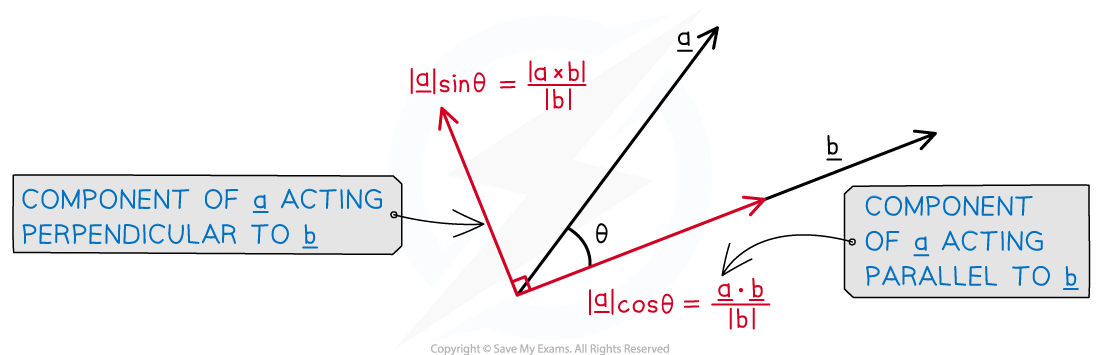
- Given a vector a acting at an angle θ to another vector b
- Draw a vector triangle by decomposing the vector a into its components parallel and perpendicular to the direction of the vector b
- The vector a will be the hypotenuse of the triangle and the two components will make up the opposite and adjacent sides
- The component of a acting parallel to b will be equal to the product of the magnitude of a and the cosine of the angle θ
- The component of a acting in the direction of b equals |a|cos θ
- This is equivalent to
- The component of a acting perpendicular to b will be equal to the product of the magnitude of a and the sine of the angle θ
- The component of a acting perpendicular to the direction of b equals |a|sin θ
- This is equivalent to
- The formulae for the components using the scalar product and the vector product are particularly useful as the angle is not needed
- The question may give you the angle the vector is acting in as a bearing
- Bearings are always the angle taken from the north
Exam Tip
- If a question asks you to find a component of a vector it is a good idea to sketch a quick diagram so that you can visualise which vectors are going in which direction
- This is especially important if the question involves forces
Worked Example
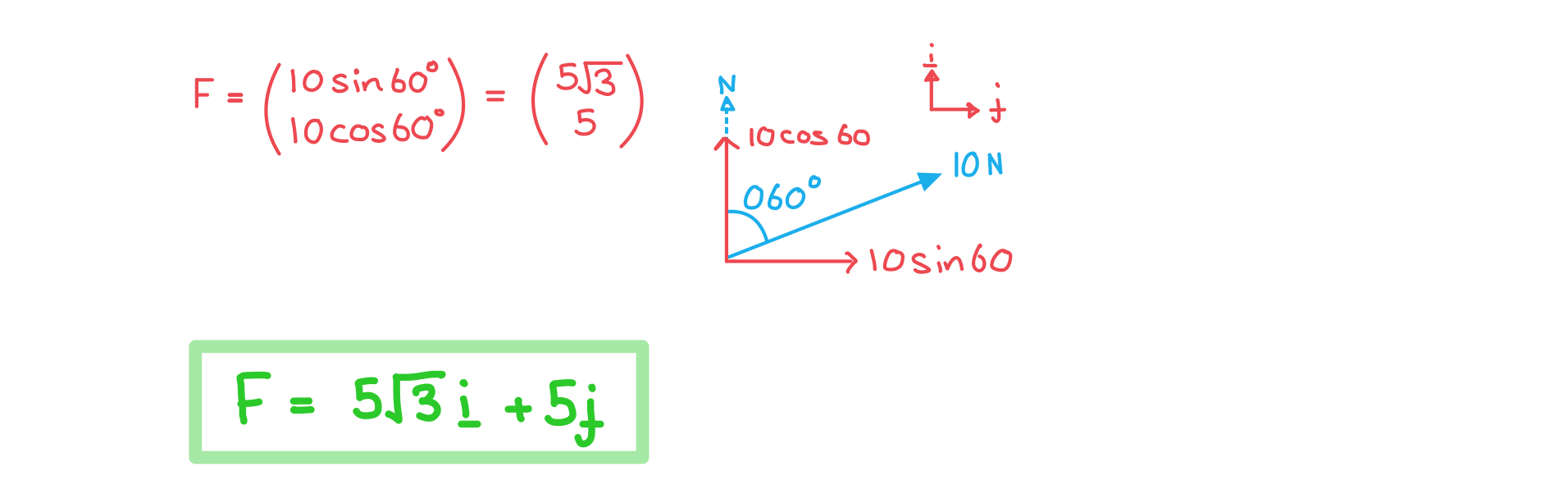
A force with magnitude 10 N is acting on a bearing of 060° on an object which is moving with velocity vector v = 2i - 3j.
a)
By finding the components of the force in the i and j direction, write down the force as a vector.
b)
Find the component of the force acting parallel to the direction of the object.

