4.12.1 Hypothesis Testing for Mean (One Sample)

One-Sample z-tests

What is a one-sample z-test?

A one-sample z-test is used to test the mean (μ) of a normally distributed population

You use a z-test when the population variance (σ²) is known

The mean of a sample of size n is calculated $\bar{x}$ and a normal distribution is used to test the test statistic
$\bar{x}$ can be used as the test statistic

In this case you would use the distribution $\bar{X} ~ N (μ, \frac{σ^{2}}{n})$

Remember when using this distribution that the standard deviation is $\frac{σ}{\sqrt{n}}$

$z = \frac{\bar{x} - μ}{\frac{σ}{\sqrt{n}}}$ can be used as the test statistic

In this case you would use the distribution $Z ~ N (0, 1^{2})$

This is a more old-fashioned approach but your GDC still might tell you the z-value when you do the test
You will not need to use this method in the exam as your GDC should be capable of doing the other method

What are the steps for performing a one-sample z-test on my GDC?

STEP 1: Write the hypotheses
- H₀: μ = μ₀
  - Clearly state that μ represents the population mean
  - μ₀is the assumed population mean

- For a one-tailed test H₁: μ < μ₀or H₁: μ > μ₀
- For a two-tailed test: H₁: μ ≠ μ₀
  - The alternative hypothesis will depend on what is being tested

STEP 2: Enter the data into your GDC and choose the one-sample z-test

If you have the raw data

Enter the data as a list
Enter the value of σ

If you have summary statistics

Enter the values of $\bar{x}$ , σ and n

Your GDC will give you the p-value

STEP 3: Decide whether there is evidence to reject the null hypothesis

If the p-value < significance level then reject H₀

STEP 4: Write your conclusion

If you reject H₀ then there is evidence to suggest that...

The mean has decreased (for H₁: μ < μ₀)
The mean has increased (for H₁: μ > μ₀)
The mean has changed (for H₁: μ ≠ μ₀)

If you accept H₀then there is insufficient evidence to reject the null hypothesis which suggests that...

The mean has not decreased (for H₁: μ < μ₀)
The mean has not increased (for H₁: μ > μ₀)
The mean has not changed (for H₁: μ ≠ μ₀)

How do I find the p-value for a one-sample z-test using a normal distribution?

The p-value is determined by the test statistic $\bar{x}$
For H₁ : μ < μ₀ the p-value is $P (\bar{X} < \bar{x} | μ = μ_{0})$
For H₁ : μ > μ₀ the p-value is $P (\bar{X} > \bar{x} | μ = μ_{0})$
For H₁ : μ ≠ μ₀ the p-value is $P (|\bar{X} - μ_{0}| > |x - μ_{0}| | μ = μ_{0})$

If $\bar{x} < μ_{0}$ then this can be calculated easier by $2 \times P (\bar{X} < \bar{x} | μ = μ_{0})$
If $\bar{x} > μ_{0}$ then this can be calculated easier by $2 \times P (\bar{X} > \bar{x} | μ = μ_{0})$

How do I find the critical value and critical region for a one-sample z-test?

The critical region is determined by the significance level α%

For H₁ : μ < μ₀ the critical region is $\bar{X} < c$ where $P (\bar{X} < c | μ = μ_{0}) = α %$
For H₁ : μ > μ₀ the critical region is $\bar{X} > c$ where $P (\bar{X} > c | μ = μ_{0}) = α %$
For H₁ : μ ≠ μ₀ the critical regions are $\bar{X} < c_{1}$ and $\bar{X} > c_{2}$ where $P (\bar{X} < c_{1} | μ = μ_{0}) = P (\bar{X} > c_{2} | μ = μ_{0}) = \frac{1}{2} α %$

The critical value(s) can be found using the inverse normal distribution function

When rounding the critical value(s) you should choose:

The lower bound for the inequalities $\bar{X} < c$
The upper bound for the inequalities $\bar{X} > c$

This is so that the probability does not exceed the significance level

Exam Tip

Exam questions might specify a method for you to use so practise all methods (using GDC, p-values, critical regions)
If the exam question does not specify a method then use whichever method you want
- Make it clear which method you are using
- You can always use a second method as a way of checking your answer

Worked Example

The mass of a Burmese cat, $C$ , follows a normal distribution with mean 4.2 kg and a standard deviation 1.3 kg. Kamala, a cat breeder, claims that Burmese cats weigh more than the average if they live in a household which contains young children. To test her claim, Kamala takes a random sample of 25 cats that live in households containing young children.

State the null and alternative hypotheses to test Kamala’s claim.

4-12-1-ib-ai-hl-one-sample-z-test-a-we-solution

Using a 5% level of significance, find the critical region for this test.

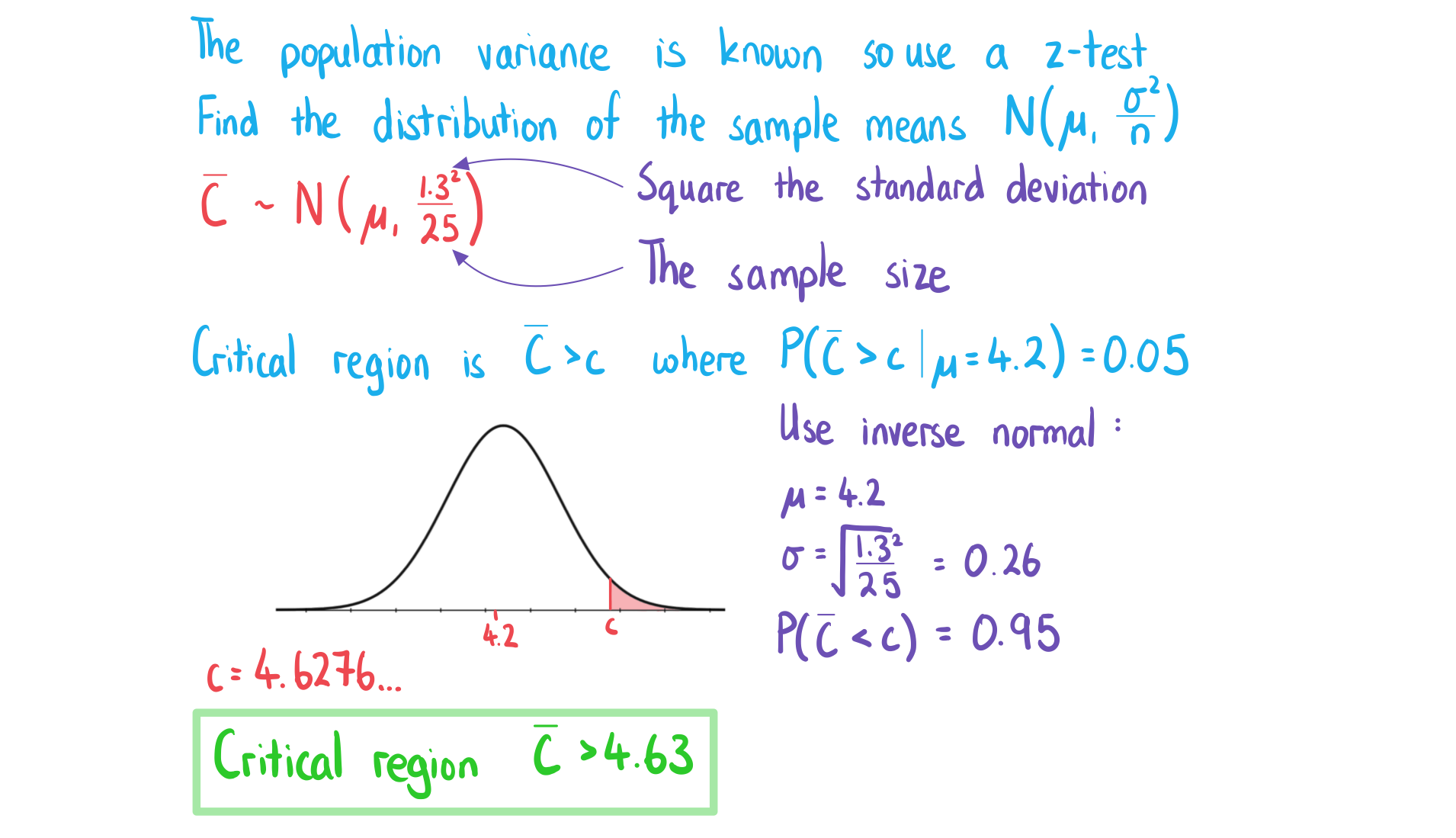
4-12-1-ib-ai-hl-one-sample-z-test-b-we-solution

Kamala calculates the mean of the 25 cats included in her sample to be 4.65 kg. Determine the conclusion of the test.

4-12-1-ib-ai-hl-one-sample-z-test-c-we-solution

One-Sample t-tests

What is a one-sample t-test?

A one-sample t-test is used to test the mean (μ) of a normally distributed population

You use a t-test when the population variance (σ²) is unknown
You need to use the unbiased estimate for the population variance ( $s_{n - 1}^{2}$ )

The mean of a sample of size n is calculated $\bar{x}$ and a t-distribution is used to test it

t-distributions are similar to normal distributions

As the sample size gets larger the t-distribution tends towards the standard normal distribution

You won’t be expected to find the critical value

The p-value can be found using the test function on your GDC

What are the steps for performing a one-sample t-test on my GDC?

STEP 1: Write the hypotheses
- H₀: μ = μ₀
  - Clearly state that μ represents the population mean
  - μ₀is the assumed population mean

- For a one-tailed test H₁: μ < μ₀or H₁: μ > μ₀
- For a two-tailed test: H₁: μ ≠ μ₀
  - The alternative hypothesis will depend on what is being tested

STEP 2: Enter the data into your GDC and choose the one-sample t-test

If you have the raw data

Enter the data as a list

If you have summary statistics

Enter the values of $\bar{x}$ , s_n-1 (sometimes written as s_x on a GDC) and n

Your GDC will give you the p-value

STEP 3: Decide whether there is evidence to reject the null hypothesis

If the p-value < significance level then reject H₀

STEP 4: Write your conclusion

If you reject H₀ then there is evidence to suggest that...

The mean has decreased (for H₁: μ < μ₀)
The mean has increased (for H₁: μ > μ₀)
The mean has changed (for H₁: μ ≠ μ₀)

If you accept H₀then there is insufficient evidence to reject the null hypothesis which suggests that...

The mean has not decreased (for H₁: μ < μ₀)
The mean has not increased (for H₁: μ > μ₀)
The mean has not changed (for H₁: μ ≠ μ₀)

Worked Example

The IQ of a student at Calculus High can be modelled as a normal distribution with mean 126. The headteacher decides to play classical music during lunchtimes and suspects that this has caused a change in the average IQ of the students.

State the null and alternative hypotheses to test the headteacher’s suspicion.

4-12-1-ib-ai-hl-one-sample-t-test-a-we-solution

The headteacher selects 15 students and asks them to complete an IQ test. The mean score for the sample is 127.1 and the sample variance is 14.7. Calculate the unbiased estimate for the population variance

s_{n - 1}^{2}

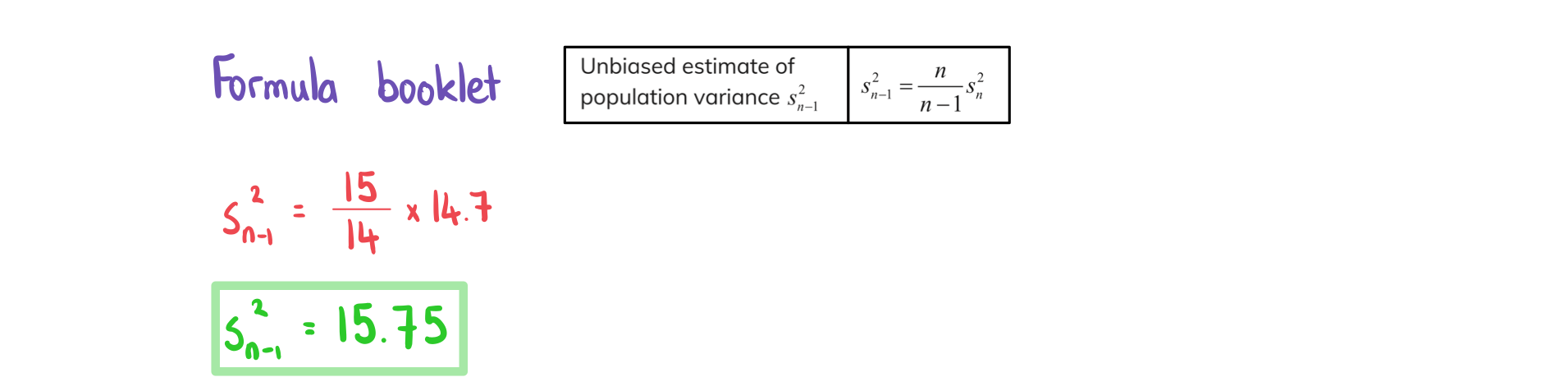
4-12-1-ib-ai-hl-one-sample-t-test-b-we-solution

Calculate the p-value for the test.

4-12-1-ib-ai-hl-one-sample-t-test-c-we-solution

State whether the headteacher’s suspicion is supported by the test.

4-12-1-ib-ai-hl-one-sample-t-test-d-we-solution

DP IB Maths: AI HL

Revision Notes

4.12.1 Hypothesis Testing for Mean (One Sample)

One-Sample z-tests

What is a one-sample z-test?

What are the steps for performing a one-sample z-test on my GDC?

How do I find the p-value for a one-sample z-test using a normal distribution?

How do I find the critical value and critical region for a one-sample z-test?

Exam Tip

Worked Example

One-Sample t-tests

What is a one-sample t-test?

What are the steps for performing a one-sample t-test on my GDC?

Worked Example

Author: Daniel

Resources

Members

Company

Quick Links