1.7.2 Operations with Matrices

Matrix Addition & Subtraction

Just as with ordinary numbers, matrices can be added together and subtracted from one another, provided that they meet certain conditions.

How is addition and subtraction performed with matrices?

Two matrices of the same order can be added or subtracted
Only corresponding elements of the two matrices are added or subtracted
- $A \pm B = (a_{i j}) \pm (b_{i j}) = (a_{i j} \pm b_{i j})$
The resultant matrix is of the same order as the original matrices being added or subtracted

What are the properties of matrix addition and subtraction?

$A + B = B + A$ (commutative)
$A + (B + C) = (A + B) + C$ (associative)
$A + O = A$
$O - A = - A$
$A - B = A + (- B)$

Exam Tip

Make sure that you know how to add and subtract matrices on your GDC for speed or for checking work in an exam!

Worked Example

Consider the matrices $A = (\begin{matrix} - 4 & 2 \\ 7 & 3 \\ 1 & - 5 \end{matrix})$ , $B = (\begin{matrix} 2 & 6 \\ 5 & - 9 \\ - 2 & - 3 \end{matrix})$ .

Find

A + B

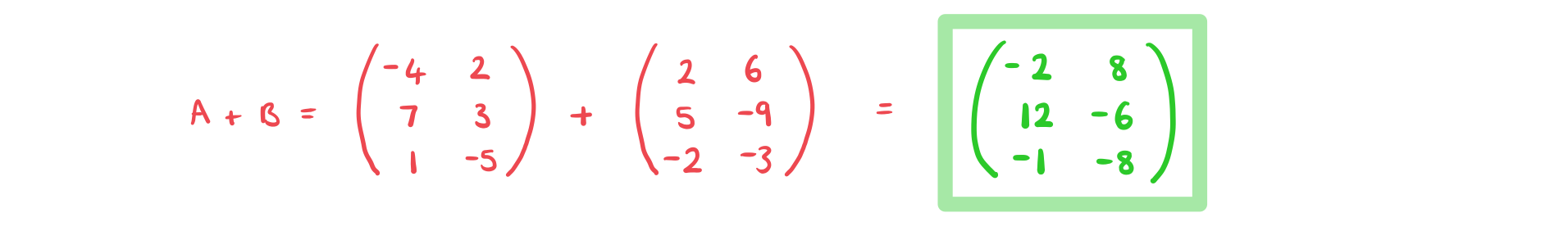
1-7-2-ib-ai-hl-operations-with-matrices-we-1a-solution

Find

A - B

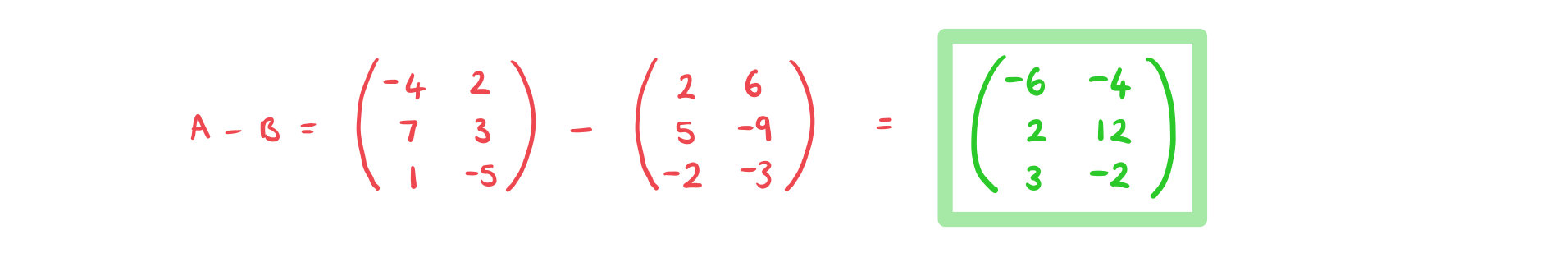
1-7-2-ib-ai-hl-operations-with-matrices-we-1b-solution

Matrix Multiplication

Matrices can also be multiplied either by a scalar or by another matrix.

How do I multiply a matrix by a scalar?

Multiply each element in the matrix by the scalar value
- $k A = (k a_{i j})$
The resultant matrix is of the same order as the original matrix
Multiplication by a negative scalar changes the sign of each element in the matrix

How do I multiply a matrix by another matrix?

To multiply a matrix by another matrix, the number of columns in the first matrix must be equal to the number of rows in the second matrix
If the order of the first matrix is $m \times n$ and the order of the second matrix is $n \times p$ , then the order of the resultant matrix will be $m \times p$
The product of two matrices is found by multiplying the corresponding elements in the row of the first matrix with the corresponding elements in the column of the second matrix and finding the sum to place in the resultant matrix

E.g. If $A = [\begin{matrix} a & b & c \\ d & e & f \end{matrix}]$ , $B = [\begin{matrix} g & h \\ i & j \\ k & l \end{matrix}]$

then $A B = [\begin{matrix} (a g + b i + c k) & (a h + b j + c l) \\ (d g + e i + f k) & (d h + e j + f l) \end{matrix}]$
then $B A = [\begin{matrix} (g a + h d) & (g b + h e) & (g c + h f) \\ (i a + j d) & (i b + j e) & (i c + j f) \\ (k a + l d) & (k b + l e) & (k c + l f) \end{matrix}]$

How do I square an expression involving matrices?

If an expression involving matrices is squared then you are multiplying the expression by itself, so write it out in bracket form first, e.g. ${(A + B)}^{2} = (A + B) (A + B)$
- remember, the regular rules of algebra do not apply here and you cannot expand these brackets, instead, add together the matrices inside the brackets and then multiply the matrices together

What are the properties of matrix multiplication?

$A B \neq B A$ (non-commutative)
$A (B C) = (A B) C$ (associative)
$A (B + C) = A B + A C$ (distributive)
$(A + B) C = A C + B C$ (distributive)
$A I = I A = A$ (identity law)
$A O = O A = O$ , where $O$ is a zero matrix
Powers of square matrices: $A^{2} = A A, A^{3} = A A A$ etc.

Exam Tip

Make sure that you are clear on the properties of matrix algebra and show each step of your calculations

Worked Example

Consider the matrices $A = [\begin{matrix} 4 & 2 & - 5 \\ - 3 & 8 & 1 \\ - 1 & - 2 & 2 \end{matrix}]$ and $B = [\begin{matrix} 5 & 1 \\ - 2 & 5 \\ 9 & 7 \end{matrix}]$ .

Find

A B

1-7-2-ib-ai-hl-operations-with-matrices-we-2a-solution

Explain why you cannot find

B A

1-7-2-ib-ai-hl-operations-with-matrices-we-2b-solution

Find

A^{2}

rn-1-7-matrices

DP IB Maths: AI HL

Revision Notes

1.7.2 Operations with Matrices

Matrix Addition & Subtraction

How is addition and subtraction performed with matrices?

What are the properties of matrix addition and subtraction?

Exam Tip

Worked Example

Matrix Multiplication

How do I multiply a matrix by a scalar?

How do I multiply a matrix by another matrix?

How do I square an expression involving matrices?

What are the properties of matrix multiplication?

Exam Tip

Worked Example

Author: Naomi

Resources

Members

Company

Quick Links