Slope Fields
What are slope fields?
- We are considering here a differential equation involving two variables of the form
- I.e., the derivative
is equal to some function of x and y
- In some cases it may be possible to solve the differential equation analytically, while in other cases this is not possible
- Whether or not the equation can be analytically solved, however, it is always possible to calculate the derivative
at any point (x, y) by putting the x and y values into
- This means that we can calculate the gradient of the solution curve at any point that the solution might go through
- A slope field for a differential equation is a diagram with short tangent lines drawn at a number of points
- The gradient of the tangent line drawn at any given point will be equal to the value of
at that point
- Normally the tangent lines will be drawn for points that form a regularly-spaced grid of x and y values

How can I use slope fields to study the solutions of a differential equation?
- Looking at the tangent lines in a slope field diagram will give you a general sense for what the solution curves to the differential equation will look like
- Remember that the solution to a given differential equation is actually a family of solutions
- We need appropriate boundary conditions or initial conditions to determine which of that family of solutions is the precise solution in a particular situation
- You can think of the tangent lines in a slope diagram as ‘flow lines’
- From a given point the solution curve through that point will ‘flow’ away from the point in the direction of the tangent line
- For a given point, you can use a slope field to sketch the general shape of the solution curve that goes through that point
- The given point here serves as a boundary condition, letting you know which of all the possible solution curves is the one you want to sketch
- The sketch should go through the given point, and follow the general ‘flow’ of the tangent lines through the rest of the slope field diagram
- In general, the sketched solution curve should not attempt to connect together a number of different tangent lines in the diagram
- There is no guarantee that the solution curve will go through any exact point in the ‘grid’ of points at which tangent lines have been drawn
- The only tangent line that your solution curve should definitely go through is one at the given ‘boundary condition’ point
- The sketched solution curve may go along some of the tangent lines, but it should not should not cut across any of them
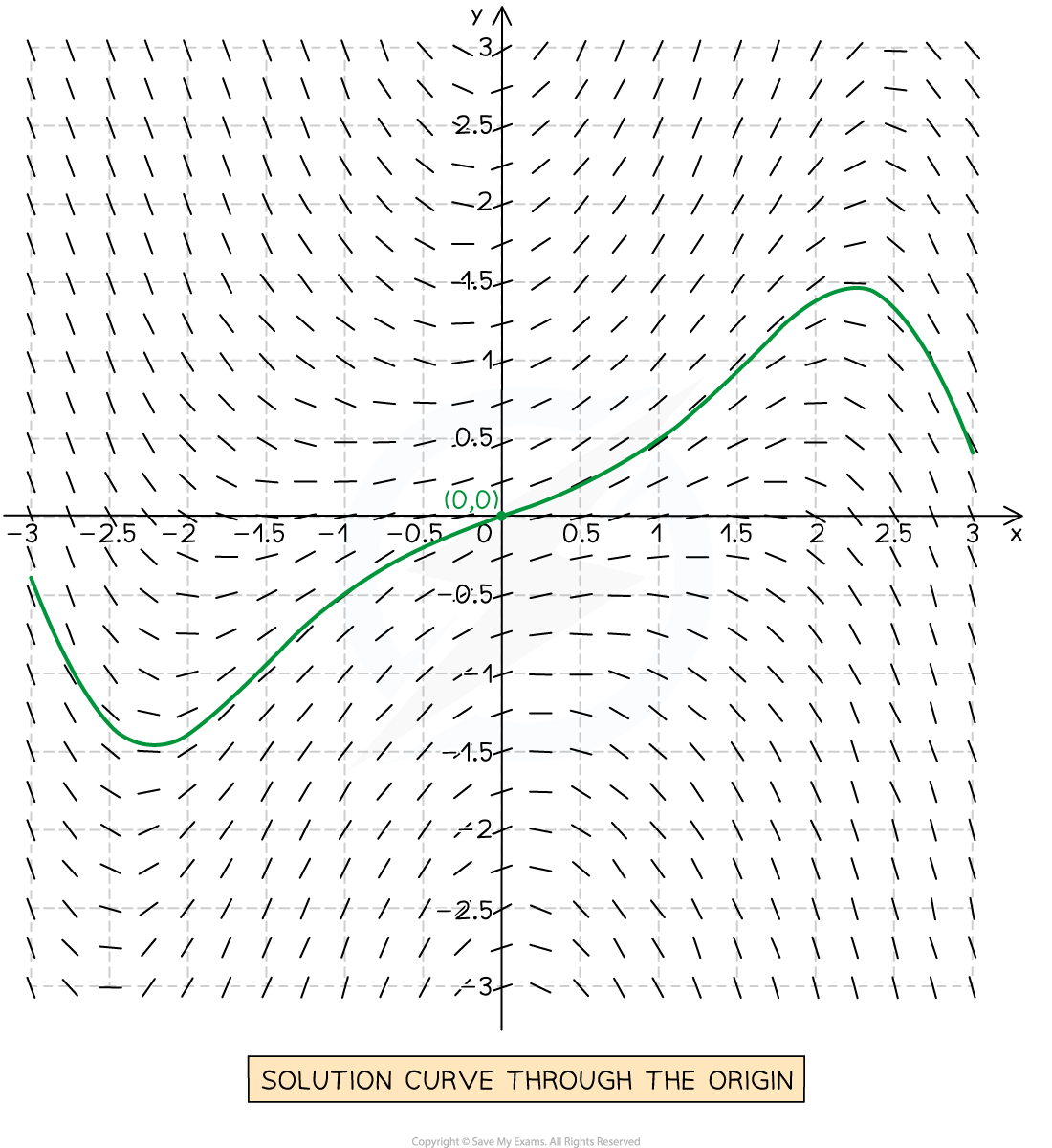
- Look out for places where the tangent lines are horizontal
- At such points
- Therefore such points may indicate local minimum or maximum points for a solution curve
- Be careful – not every point where
is a local minimum or maximum
- But every local minimum or maximum will be at a point where
- Don’t forget that you can also solve the equation
directly to identify points where the gradient is zero
- For example if
, then the gradient will be zero anywhere where
- This is another way to identify possible local minimum and maximum points for the solution curves
- If such a point falls between the ‘grid points’ at which the tangent lines have been drawn, this may be the only way to identify such a point exactly
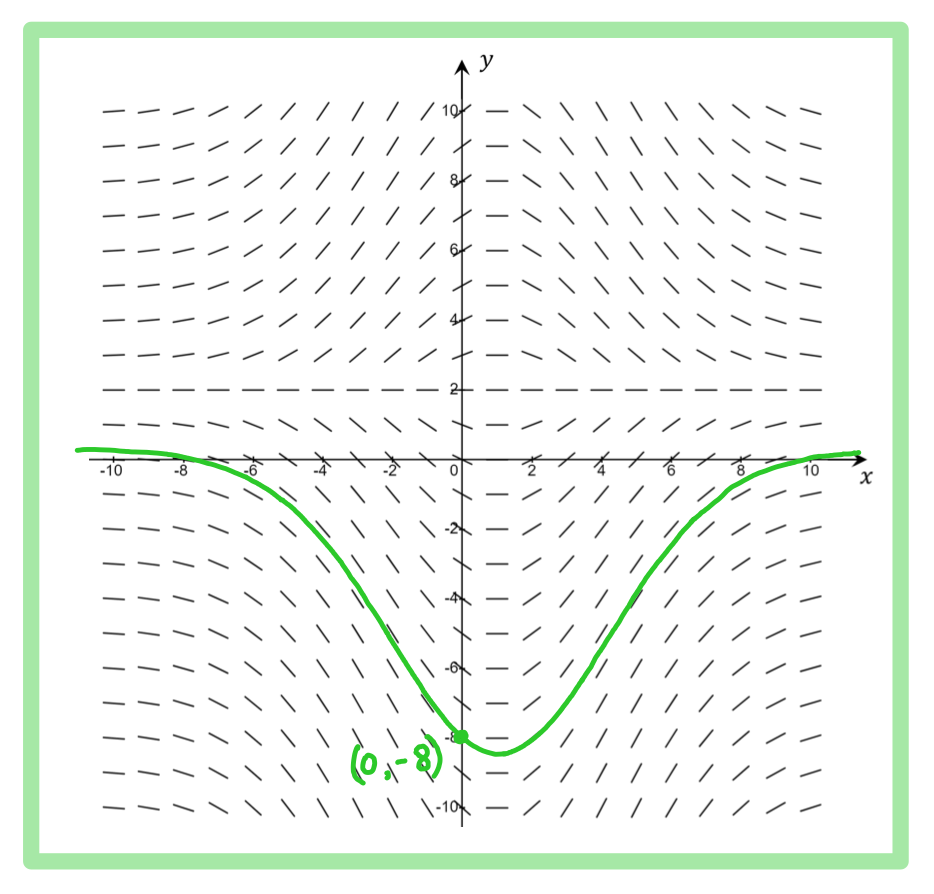
Worked Example
Consider the differential equation
.
a)
Using the equation, determine the set of points for which the solutions to the differential equation will have horizontal tangents.

The diagram below shows the slope field for the differential equation, for and
.

b)
Sketch the solution curve for the solution to the differential equation that passes through the point .