Name: Logarithmic Scales (4.3.2) | DP IB Maths: AI HL Revision Notes 2021 Membership
Brand: Save My Exams
Price: 60 GBP
Availability: OnlineOnly
Rating: 4.7 (1021 reviews)

4.3.2 Logarithmic Scales

Logarithmic Scales

What are logarithmic scales?

Logarithmic scales are scales where intervals increase exponentially
- A normal scale might go 1, 2, 3, 4, ...
- A logarithmic scale might go 1, 10, 100, 1000, ...
Sometimes we can keep the scales with constant intervals by changing the variables
- If the values of x increase exponentially: 1, 10, 100, 1000, ...
- Then you can use the variable log x instead which will have the scale: 1, 2, 3, 4, ...
- This will change the shape of the graph
  - If the graph transforms to a straight line then it is easier to analyse
Any base can be used for logarithmic scales
- The most common bases are 10 and e

Why do we use logarithmic scales?

For variables that have a large range it can be difficult to plot on one graph

Especially when a lot of the values are clustered in one region
For example: populations of countries

This can range from 800 to 1 450 000 000

If we are interested in the rate of growth of a variable rather than the actual values then a logarithmic scale is useful

log-log & semi-log Graphs

What is a log-log graph?

A log-log graph is used when both scales of the original graph are logarithmic
- You transform both variables by taking logarithms of the values
log y & log x will be used instead of y & x
Power graphs ( $y = a x^{b}$ ) look like straight lines on log-log graphs

What is a semi-log graph?

A semi-log graph is used when only one scale (the y-axis) of the original graph are logarithmic
- You transform only the y-variable by taking logarithms of those values
log y will be used instead of y
Exponential graphs ( $y = a b^{x}$ ) look like straight lines on semi-log graphs

How can I estimate values using log-log and semi-log graphs?

Identify whether one or both of the scales are logarithmic
Identify the variable so that the scales have equal intervals
- x : 1, 10, 100, 1000, ... use log x
- For x : 1, e, e², e³, ... use ln x
If you are asked to estimate a value:
- First find the value of any logarithms
  - For example: log y, ln x, etc
- Use the graph to read off the value
- If it is a value for a logarithm find the actual value using:
  - $\log x = k \Rightarrow x = 10^{k}$
  - $\ln x = k \Rightarrow x = e^{k}$

Exam Tip

Pay close attention to which base is being used (log or ln)

Worked Example

The function $y = f (x)$ is drawn below using a log-log graph.

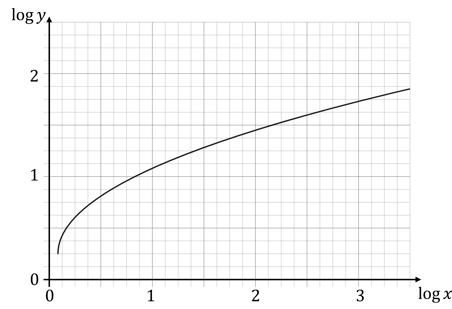2-7-1-we-image Show that when $x = 56$ the value of $y$ is approximately 24.

2-7-1-ib-ai-hl-log-log-graphs-we-solution

DP IB Maths: AI HL

Revision Notes

4.3.2 Logarithmic Scales

Logarithmic Scales

What are logarithmic scales?

Why do we use logarithmic scales?

log-log & semi-log Graphs

What is a log-log graph?

What is a semi-log graph?

How can I estimate values using log-log and semi-log graphs?

Exam Tip

Worked Example

Author: Daniel

Resources

Members

Company

Quick Links