Modulus & Argument
How do I find the modulus of a complex number?
- The modulus of a complex number is its distance from the origin when plotted on an Argand diagram
- The modulus of
is written
- If
, then we can use Pythagoras to show…
- A modulus is never negative
What features should I know about the modulus of a complex number?
- the modulus is related to the complex conjugate by…
- This is because
- In general,
- e.g. both
and
have a modulus of 5, but
simplifies to 8i which has a modulus of 8
- e.g. both
How do I find the argument of a complex number?
- The argument of a complex number is the angle that it makes on an Argand diagram
- The angle must be taken from the positive real axis
- The angle must be in a counter-clockwise direction
- Arguments are measured in radians
- They can be given exact in terms of
- They can be given exact in terms of
- The argument of
is written
- Arguments can be calculated using right-angled trigonometry
- This involves using the tan ratio plus a sketch to decide whether it is positive/negative and acute/obtuse
What features should I know about the argument of a complex number?
- Arguments are usually given in the range
- Negative arguments are for complex numbers in the third and fourth quadrants
- Occasionally you could be asked to give arguments in the range
- The question will make it clear which range to use
- The argument of zero,
is undefined (no angle can be drawn)
What are the rules for moduli and arguments under multiplication and division?
- When two complex numbers,
and
, are multiplied to give
, their moduli are also multiplied
- When two complex numbers,
and
, are divided to give
, their moduli are also divided
- When two complex numbers,
and
, are multiplied to give
, their arguments are added
- When two complex numbers,
and
, are divided to give
, their arguments are subtracted
Exam Tip
- Always draw a quick sketch to help you see what quadrant the complex number lies in when working out an argument
- Look for the range of values within which you should give your argument
- If it is
then you may need to measure it in the negative direction
- If it is
then you will always measure in the positive direction (counter - clockwise)
- If it is
Worked Example
a)
Find the modulus and argument of format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%224.5%22%20y%3D%2216%22%3Ez%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1564b4c0e54101ac57a0cb68c16%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2217.5%22%20y%3D%2216%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2230.5%22%20y%3D%2216%22%3E2%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1564b4c0e54101ac57a0cb68c16%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2243.5%22%20y%3D%2216%22%3E%2B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2256.5%22%20y%3D%2216%22%3E3%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2263.5%22%20y%3D%2216%22%3Ei%3C%2Ftext%3E%3C%2Fsvg%3E)
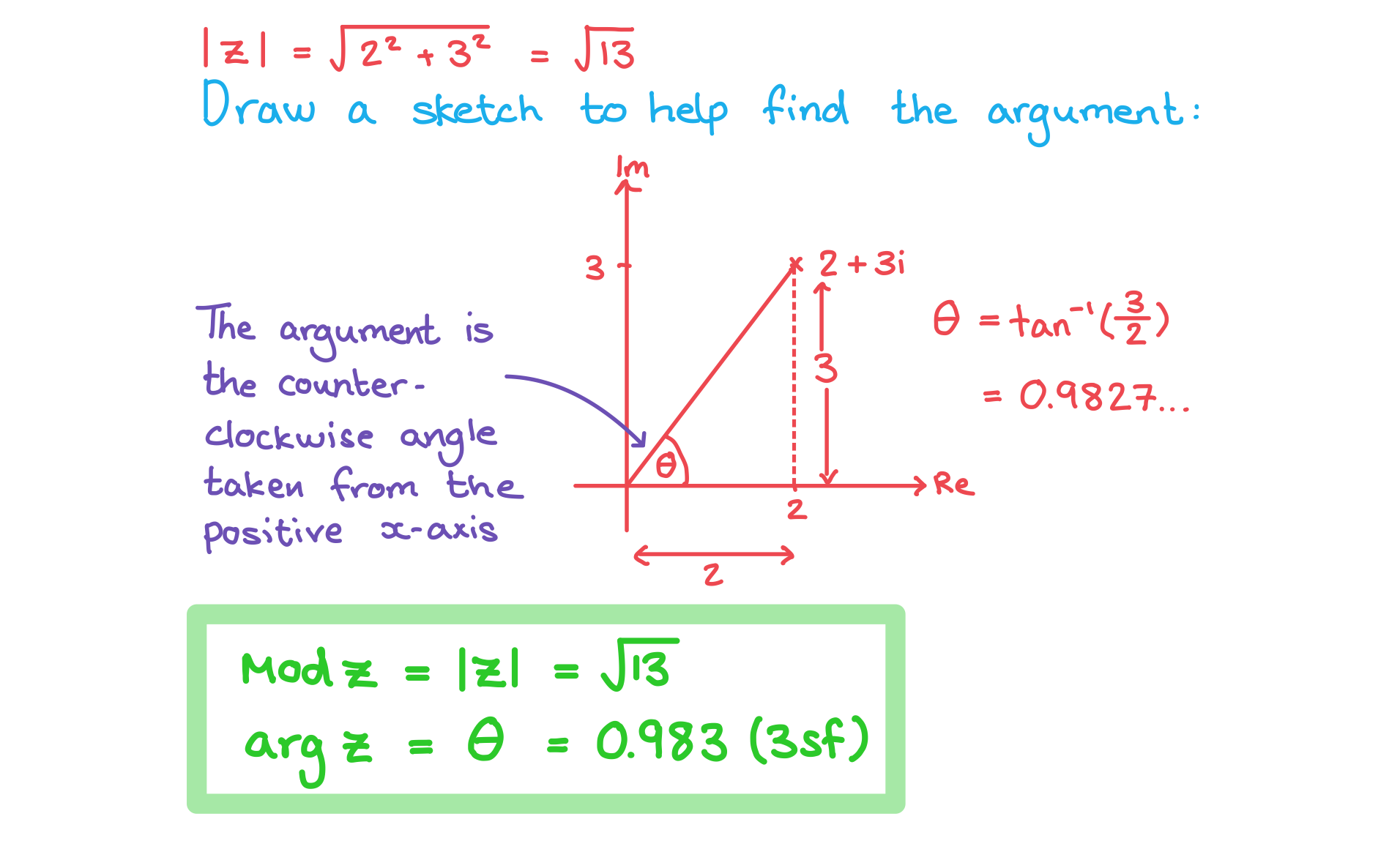
b)
Find the modulus and argument of format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%226.5%22%20y%3D%2220%22%3Ew%3C%2Ftext%3E%3Ctext%20font-family%3D%22math143f4d31b04031e49f5eb18baba%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2222.5%22%20y%3D%2220%22%3E%3D%3C%2Ftext%3E%3Ctext%20font-family%3D%22math143f4d31b04031e49f5eb18baba%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2239.5%22%20y%3D%2220%22%3E%26%23x2212%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2252.5%22%20y%3D%2220%22%3E1%3C%2Ftext%3E%3Ctext%20font-family%3D%22math143f4d31b04031e49f5eb18baba%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2265.5%22%20y%3D%2220%22%3E%26%23x2212%3B%3C%2Ftext%3E%3Cpolyline%20fill%3D%22none%22%20points%3D%2214%2C-19%2013%2C-19%206%2C0%202%2C-7%22%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20transform%3D%22translate(74.5%2C23.5)%22%2F%3E%3Cpolyline%20fill%3D%22none%22%20points%3D%226%2C0%202%2C-7%201%2C-6%22%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20transform%3D%22translate(74.5%2C23.5)%22%2F%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2288.5%22%20x2%3D%22100.5%22%20y1%3D%224.5%22%20y2%3D%224.5%22%2F%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%2294.5%22%20y%3D%2220%22%3E3%3C%2Ftext%3E%3Ctext%20font-family%3D%22Times%20New%20Roman%22%20font-size%3D%2218%22%20text-anchor%3D%22middle%22%20x%3D%22103.5%22%20y%3D%2220%22%3Ei%3C%2Ftext%3E%3C%2Fsvg%3E)

