2.6.4 Piecewise Models

Linear Piecewise Models

What are the parameters of a piecewise linear model?

A piecewise linear model is made up of multiple linear models $f_{i} (x) = m_{i} x + c_{i}$
For each linear model there will be
- The rate of change for that interval m_i
- The value if the independent variable was not present c_i

What can be modelled as a piecewise linear model?

Piecewise linear models can be used when the rate of change of a function changes for different intervals
- These commonly apply when there are different tariffs or levels of charges
Anything with a constant rate of change for set intervals
- C(d) is the taxi charge for a journey of d km
  - The charge might double after midnight
- R(d) is the rental fee for a car used for d days
  - The daily fee might triple if the car is rented over bank holidays
- s(t) is the speed of a car travelling for t seconds with constant acceleration
  - The car might reach a maximum speed

What are possible limitations of a piecewise linear model?

Linear models have a constant rate of change
- In real-life this might not be the case
- A function might increase (or decrease) gradually rather than at a constant rate

Exam Tip

Make sure that you know how to plot a piecewise model on your GDC

Worked Example

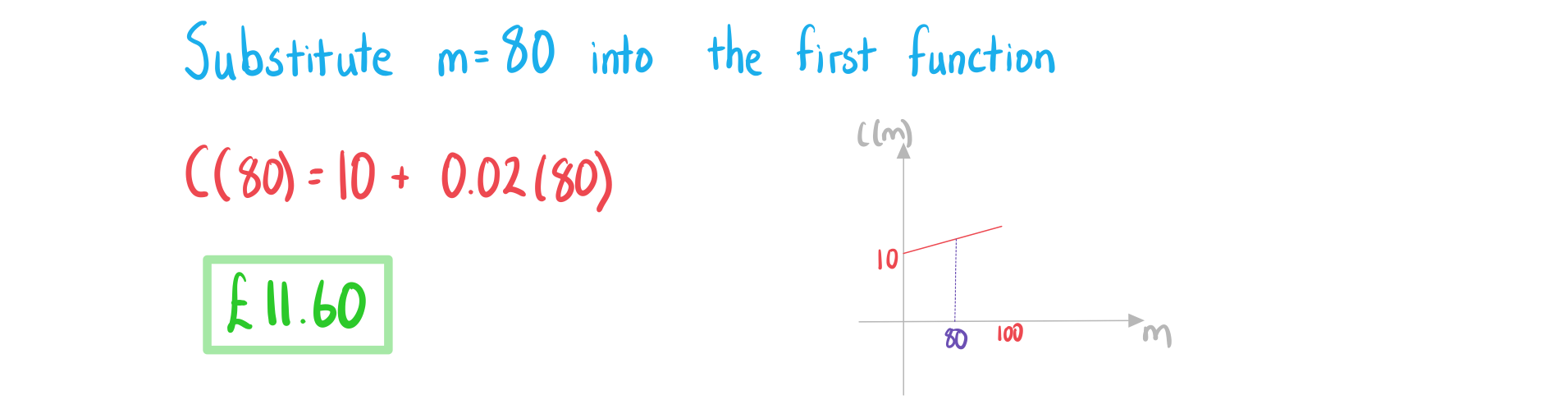
The total monthly charge, $£ C$ , of phone bill can be modelled by the function

$C (m) = \{\begin{matrix} 10 + 0.02 m \\ 9 + 0.03 m \end{matrix} \begin{matrix} 0 \leq m \leq 100 \\ m > 100 \end{matrix}$ ,

where $m$ is the number of minutes used.

Find the total monthly charge if 80 minutes have been used.

2-3-1-ib-ai-sl-piecewise-models-a-we-solution

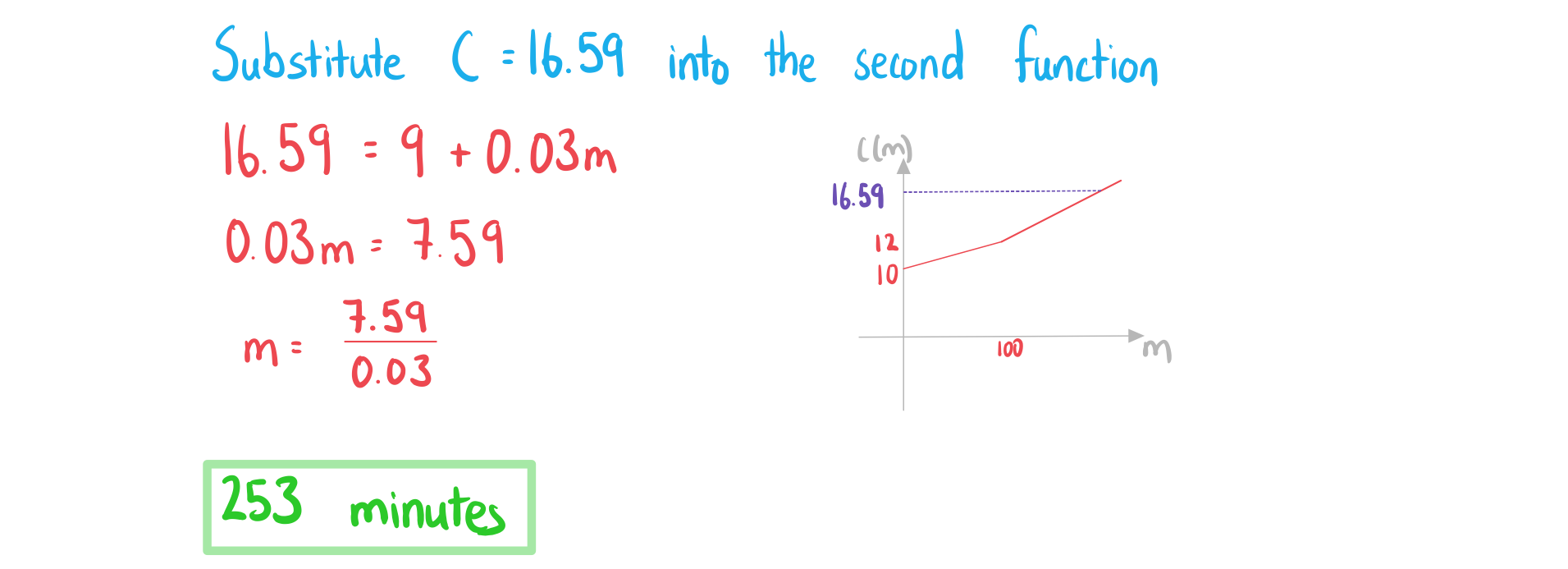
Given that the total monthly charge is £16.59, find the number of minutes that were used.

2-3-1-ib-ai-sl-piecewise-models-b-we-solution

Non-Linear Piecewise Models

What are the parameters of non-linear piecewise models?

A non-linear piecewise model is made up of multiple functions $f_{i} (x)$

Each function will be defined for a range of values of x

The individual functions can contain any function

For example: quadratic, cubic, exponential, etc

When graphed the individual functions should join to make a continuous graph

This fact can be used to find unknown parameters

If $f (x) = \{\begin{matrix} f_{1} (x) \\ f_{2} (x) \end{matrix} \begin{matrix} a \leq x < b \\ b \leq x < c \end{matrix}$ then $f_{1} (b) = f_{2} (b)$

What can be modelled as a non-linear piecewise model?

Piecewise models can be used when different functions are needed to represent the output for different intervals of the variable

S(x) is the standardised score on a test with x raw marks

For small values of x there might be a quadratic model
For large values of x there might be a linear model

H(t) is the height of water in a bathtub with after t minutes

Initially a cubic model might be a appropriate if the bottom of the bathtub is curved
Then a linear model might be a appropriate if the sides of top of the bathtub has the shape of a prism

What are possible limitations a non-linear piecewise model?

Piecewise models can be used to model real-life accurately
Piecewise models can be difficult to analyse or apply mathematical techniques to

Exam Tip

Read and re-read the question carefully, try to get involved in the context of the question!
Pay particular attention to the domain of each section, if it is not given think carefully about any restrictions there may be as a result of the context of the question
If sketching a piecewise function, make sure to include the coordinates of all key points including the point at which two sections of the piecewise model meet

Worked Example

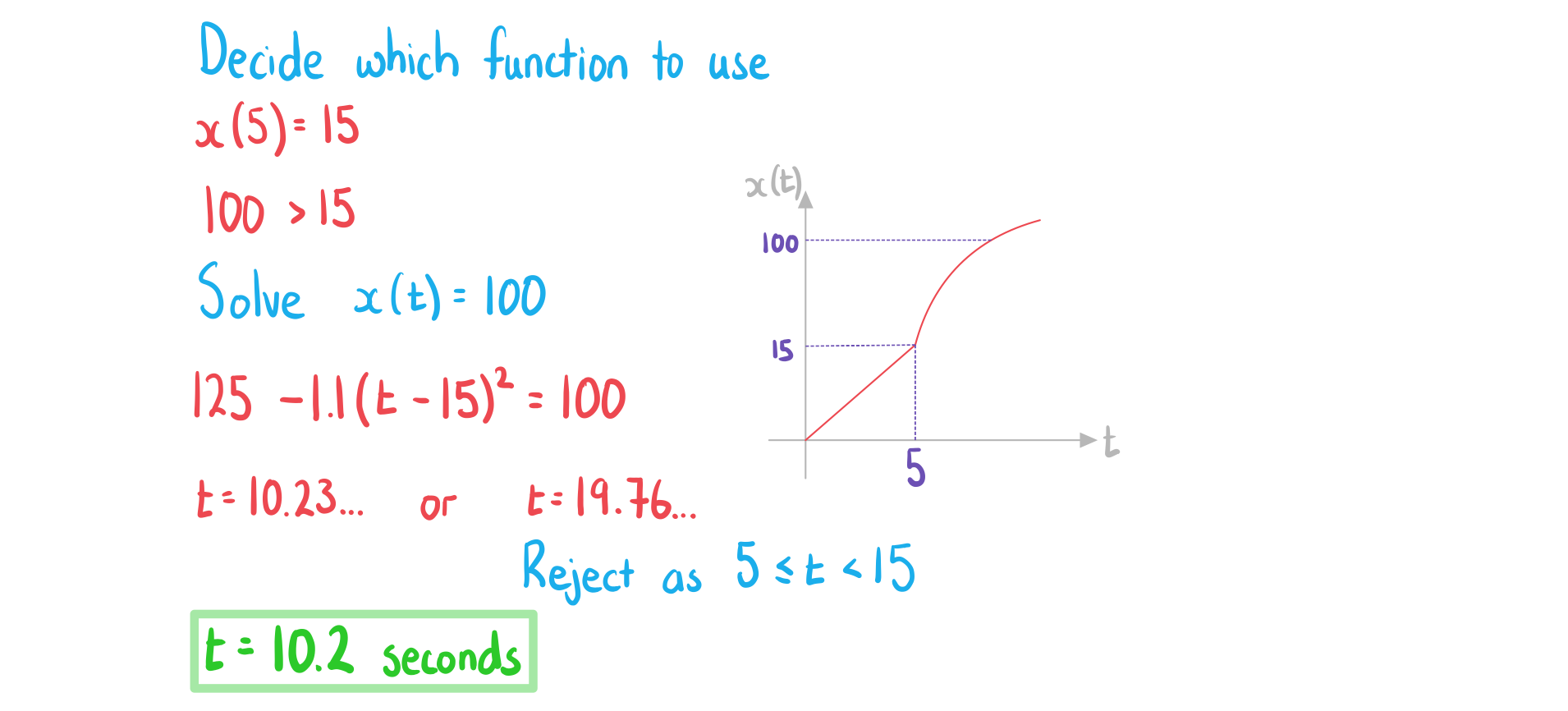
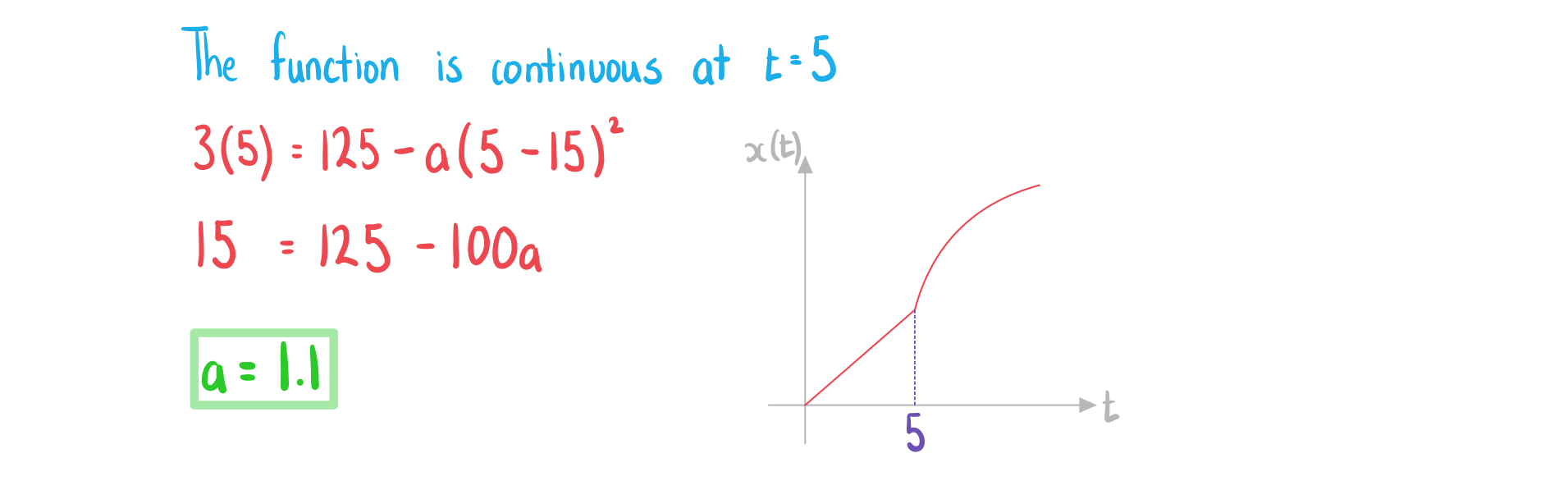
Jamie is running a race. His distance from the start, $x$ metres, can be modelled by the function

$x (t) = \{\begin{matrix} 3 t \\ 125 - a (t - 15) ² \end{matrix} \begin{matrix} 0 \leq t < 5 \\ 5 \leq t < 15 \end{matrix}$

where $t$ is the time, in seconds, elapsed since the start of the race.

Find the value of

a

2-6-4-ib-ai-hl-nonlinear-piecewise-model-a-we-solution

Find the time taken for Jamie to reach 100 metres from the start.

2-6-4-ib-ai-hl-nonlinear-piecewise-model-b-we-solution

DP IB Maths: AI HL

Revision Notes

2.6.4 Piecewise Models

Linear Piecewise Models

What are the parameters of a piecewise linear model?

What can be modelled as a piecewise linear model?

What are possible limitations of a piecewise linear model?

Exam Tip

Worked Example

Non-Linear Piecewise Models

What are the parameters of non-linear piecewise models?

What can be modelled as a non-linear piecewise model?

What are possible limitations a non-linear piecewise model?

Exam Tip

Worked Example

Author: Daniel

Resources

Members

Company

Quick Links