| Date | May 2011 | Marks available | 3 | Reference code | 11M.2.sl.TZ2.5 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Show and Complete | Question number | 5 | Adapted from | N/A |
Question
There is a vertical tower TA of height 36 m at the base A of a hill. A straight path goes up the hill from A to a point U. This information is represented by the following diagram.
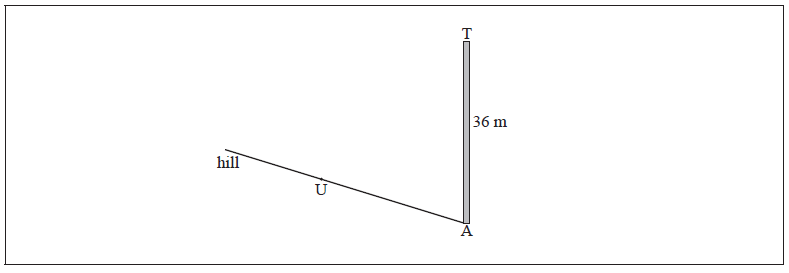
The path makes a \({4^ \circ }\) angle with the horizontal.
The point U on the path is \(25{\text{ m}}\) away from the base of the tower.
The top of the tower is fixed to U by a wire of length \(x{\text{ m}}\).
Complete the diagram, showing clearly all the information above.
Find x .
Markscheme
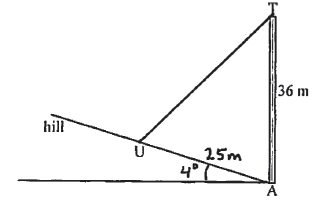A1A1A1 N3
Note: Award A1 for labelling \({4^ \circ }\) with horizontal, A1 for labelling [AU] 25 metres, A1 for drawing [TU].
[3 marks]
\({\rm{T}}\widehat {\rm{A}}{\rm{U}} = {86^ \circ }\) (A1)
evidence of choosing cosine rule (M1)
correct substitution A1
e.g. \({x^2} = {25^2} + {36^2} - 2(25)(36)\cos {86^ \circ }\)
\(x = 42.4\) A1 N3
[4 marks]
Examiners report
This question was attempted in a satisfactory manner. Even the weakest candidates earned some marks here, showing some clear working. In part (a) the diagram was completed fairly well, with some candidates incorrectly labelling the angle with the vertical as \({4^ \circ }\) . The cosine rule was applied satisfactory in part (b), although some candidates incorrectly used their calculators in radian mode. Approaches using a combination of the sine rule and/or right-angled triangle trigonometry were seen, especially when candidates incorrectly labelled the \(25{\text{ m}}\) path as being the distance from the horizontal to U.
This question was attempted in a satisfactory manner. Even the weakest candidates earned some marks here, showing some clear working. In part (a) the diagram was completed fairly well, with some candidates incorrectly labelling the angle with the vertical as \({4^ \circ }\) . The cosine rule was applied satisfactory in part (b), although some candidates incorrectly used their calculators in radian mode. Approaches using a combination of the sine rule and/or right-angled triangle trigonometry were seen, especially when candidates incorrectly labelled the \(25{\text{ m}}\) path as being the distance from the horizontal to U.
