| Date | November 2010 | Marks available | 3 | Reference code | 10N.2.sl.TZ0.6 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
The following diagram shows the triangle ABC.
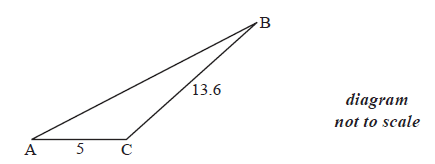
The angle at C is obtuse, \({\text{AC}} = 5{\text{ cm}}\), \({\text{BC}} =13.6{\text{ cm}}\) and the area is \(20{\text{ c}}{\text{m}}^2\) .
Find \({\rm{A}}\widehat {\rm{C}}{\rm{B}}\) .
Find AB.
Markscheme
correct substitution into the formula for the area of a triangle A1
e.g. \(\frac{1}{2} \times 5 \times 13.6 \times \sin C = 20\) , \(\frac{1}{2} \times 5 \times h = 20\)
attempt to solve (M1)
e.g. \(\sin C = 0.5882 \ldots \) , \(\sin C = \frac{8}{{13.6}}\)
\(\widehat C = 36.031 \ldots ^\circ \) (\(0.6288 \ldots {\text{ radians}}\)) (A1)
\({\rm{A}}\widehat {\rm{C}}{\rm{B}} = 144^\circ \) \((2.51{\text{ radians}})\) A1 N3
[4 marks]
evidence of choosing the cosine rule (M1)
correct substitution A1
e.g. \({({\rm{AB}})^2} = {5^2} + {13.6^2} - 2(5)(13.6)\cos 143.968 \ldots \)
\({\text{AB}} = 17.9\) A1 N2
[3 marks]
Examiners report
Part (a) was well done with the majority of candidates obtaining the acute angle. Unfortunately, the question asked for the obtuse angle which was clearly stated and shown in the diagram. No matter which angle was used, most candidates were able to obtain full marks in part (b) with a simple application of the cosine rule.
Part (a) was well done with the majority of candidates obtaining the acute angle. Unfortunately, the question asked for the obtuse angle which was clearly stated and shown in the diagram. No matter which angle was used, most candidates were able to obtain full marks in part (b) with a simple application of the cosine rule.

