| Date | November 2014 | Marks available | 3 | Reference code | 14N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows a circle with centre \(O\) and radius \(8\) cm.
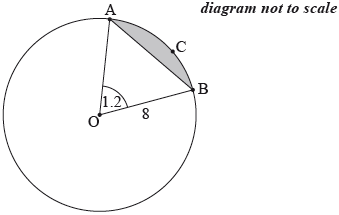
The points \(A\), \(B\) and \(C\) are on the circumference of the circle, and \({\rm{A\hat OB}}\) radians.
Find the length of arc \(ACB\).
Find \(AB\).
Hence, find the perimeter of the shaded segment \(ABC\).
Markscheme
correct substitution into formula (A1)
eg\(\;\;\;\)\(l = 1.2 \times 8\)
\(9.6{\text{ (cm)}}\) A1 N2
[2 marks]
METHOD 1
evidence of choosing cosine rule (M1)
eg\(\;\;\;\)\(2{r^2} - 2 \times {r^2} \times \cos ({\rm{A\hat OB)}}\)
correct substitution into right hand side (A1)
eg\(\;\;\;\)\({8^2} + {8^2} - 2 \times 8 \times 8 \times \cos (1.2)\)
\(9.0342795\)
\({\text{AB}} = 9.03{\text{ }}[9.03,{\text{ }}9.04]{\text{ (cm)}}\) A1 N2
METHOD 2
evidence of choosing sine rule (M1)
eg\(\;\;\;\)\(\frac{{{\text{AB}}}}{{\sin ({\rm{A\hat OB)}}}} = \frac{{{\text{OB}}}}{{\sin ({\rm{O\hat AB)}}}}\)
finding angle \(OAB\) or \(OBA\) (may be seen in substitution) (A1)
eg\(\;\;\;\)\(\frac{{\pi - 1.2}}{2},{\text{ }}0.970796\)
\({\text{AB}} = 9.03{\text{ }}[9.03,{\text{ }}9.04]{\text{ (cm)}}\) A1 N2
[3 marks]
correct working (A1)
eg\(\;\;\;\)\(P = 9.6 + 9.03\)
\(18.6342\)
\(18.6{\text{ }}[18.6,{\text{ }}18.7]{\text{ (cm)}}\) A1 N2
[2 marks]
Total [7 marks]
Examiners report
Parts (a) and (b) were well done, but it was not uncommon to see students finding area instead of perimeter in part (c). Most candidates recognized the need to use the cosine rule in part (b), and other candidates chose to use the sine rule to find the length of AB.
There are candidates who do not seem comfortable working with radians and transform the angles into degrees. Other candidates used an angle of \(1.2\pi \) instead of 1.2, supposing that angles in radians always should have \(\pi \).
Parts (a) and (b) were well done, but it was not uncommon to see students finding area instead of perimeter in part (c). Most candidates recognized the need to use the cosine rule in part (b), and other candidates chose to use the sine rule to find the length of AB.
There are candidates who do not seem comfortable working with radians and transform the angles into degrees. Other candidates used an angle of \(1.2\pi \) instead of 1.2, supposing that angles in radians always should have \(\pi \).
Parts (a) and (b) were well done, but it was not uncommon to see students finding area instead of perimeter in part (c). Most candidates recognized the need to use the cosine rule in part (b), and other candidates chose to use the sine rule to find the length of AB.
There are candidates who do not seem comfortable working with radians and transform the angles into degrees. Other candidates used an angle of \(1.2\pi \) instead of 1.2, supposing that angles in radians always should have \(\pi \).

