| Date | May 2009 | Marks available | 3 | Reference code | 09M.2.sl.TZ2.4 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The diagram below shows a triangle ABD with AB =13 cm and AD = 6.5 cm.
Let C be a point on the line BD such that BC = AC = 7 cm.
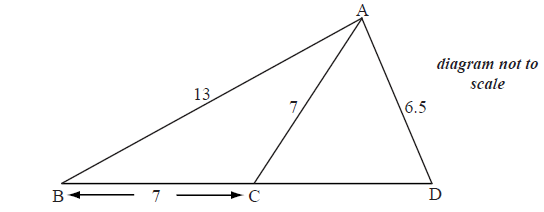
Find the size of angle ACB.
Find the size of angle CAD.
Markscheme
METHOD 1
evidence of choosing the cosine formula (M1)
correct substitution A1
e.g. \(\cos {\rm{A}}\widehat {\rm{C}}{\rm{B}} = \frac{{{7^2} + {7^2} - {{13}^2}}}{{2 \times 7 \times 7}}\)
\({\rm{A}}\widehat {\rm{C}}{\rm{B}} = 2.38\) radians \(( = 136^\circ )\) A1 N2
METHOD 2
evidence of appropriate approach involving right-angled triangles (M1)
correct substitution A1
e.g. \(\sin \left( {\frac{1}{2}{\rm{A}}\widehat {\rm{C}}{\rm{B}}} \right) = \frac{{6.5}}{7}\)
\({\rm{A}}\widehat {\rm{C}}{\rm{B}} = 2.38\) radians \(( = 136^\circ )\) A1 N2
[3 marks]
METHOD 1
\({\rm{A}}\widehat {\rm{C}} {\rm{D}} = \pi - 2.381\) \((180 - 136.4)\) (A1)
evidence of choosing the sine rule in triangle ACD (M1)
correct substitution A1
e.g. \(\frac{{6.5}}{{\sin 0.760 \ldots }} = \frac{7}{{\sin {\rm{A}}\widehat {\rm{D}} {\rm{C}}}}\)
\({\rm{A}}\widehat {\rm{D}}{\rm{C}} = 0.836 \ldots \) \(( = 47.9 \ldots ^\circ )\) A1
\({\rm{C}}\widehat {\rm{A}}{\rm{D}} = \pi - (0.760 \ldots + 0.836 \ldots )\) \((180 - (43.5 \ldots + 47.9 \ldots ))\)
\( = 1.54\) \(( = 88.5^\circ )\) A1 N3
METHOD 2
\({\rm{A}}\widehat {\rm{B}}{\rm{C}} = \frac{1}{2}(\pi - 2.381)\) \(\left( {\frac{1}{2}(180 - 136.4)} \right)\) (A1)
evidence of choosing the sine rule in triangle ABD (M1)
correct substitution A1
e.g. \(\frac{{6.5}}{{\sin 0.380 \ldots }} = \frac{{13}}{{\sin {\rm{A}}\widehat {\rm{D}}{\rm{C}}}}\)
\({\rm{A}}\widehat {\rm{D}}{\rm{C}} = 0.836 \ldots \) \(( = 47.9 \ldots ^\circ )\) A1
\({\rm{C}}\widehat {\rm{A}}{\rm{D}} = \pi - 0.836 \ldots - (\pi - 2.381 \ldots )\) \(( = 180 - 47.9 \ldots - (180 - 136.4))\)
\( = 1.54\) \(( = 88.5^\circ )\) A1 N3
Note: Two triangles are possible with the given information. If candidate finds \({\rm{A}}\widehat {\rm{D}}{\rm{C}} = 2.31\) \((132^\circ )\) leading to \({\rm{C}}\widehat {\rm{A}}{\rm{D}} = 0.076\) \((4.35^\circ )\) , award marks as per markscheme.
[5 marks]
Examiners report
This question was generally well done. Even the weakest candidates often earned marks. Only a very few candidates used a right-angled triangle approach.
Almost no candidates realized there was an ambiguous case of the sine rule in part (b). Those who did not lose the mark for accuracy in the previous question often lost it here.

