| Date | May 2011 | Marks available | 3 | Reference code | 11M.2.sl.TZ1.1 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows triangle ABC .
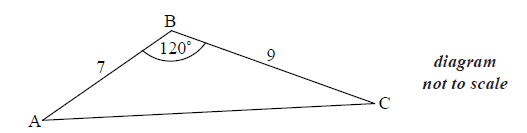
AB = 7 cm, BC = 9 cm and \({\rm{A}}\widehat {\rm{B}}{\rm{C}} = {120^ \circ }\) .
Find AC .
Find \({\rm{B}}\widehat {\rm{A}}{\rm{C}}\) .
Markscheme
evidence of choosing cosine rule (M1)
e.g. \({a^2} + {b^2} - 2ab\cos C\)
correct substitution A1
e.g. \({7^2} + {9^2} - 2(7)(9)\cos {120^ \circ }\)
\({\text{AC}} = 13.9\) \(\left( { = \sqrt {193} } \right)\) A1 N2
[3 marks]
METHOD 1
evidence of choosing sine rule (M1)
e.g. \(\frac{{\sin \widehat A}}{{{\rm{BC}}}} = \frac{{\sin \widehat B}}{{{\rm{AC}}}}\)
correct substitution A1
e.g. \(\frac{{\sin \widehat A}}{9} = \frac{{\sin 120}}{{13.9}}\)
\(\widehat A = {34.1^ \circ }\) A1 N2
METHOD 2
evidence of choosing cosine rule (M1)
e.g. \(\cos \widehat A = \frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} - {\rm{B}}{{\rm{C}}^2}}}{{2({\rm{AB}})({\rm{AC}})}}\)
correct substitution A1
e.g. \(\cos \widehat A = \frac{{{7^2} + {{13.9}^2} - {9^2}}}{{2(7)(13.9)}}\)
\(\widehat A = {34.1^ \circ }\) A1 N2
[3 marks]
Examiners report
The majority of candidates were successful with this question. Most correctly used the cosine rule in part (a) and the sine rule in part (b). Some candidates did not check that their GDC was set in degree mode while others treated the triangle as if it were right angled. A large number of candidates were penalized for not leaving their answers exactly or to three significant figures.
The majority of candidates were successful with this question. Most correctly used the cosine rule in part (a) and the sine rule in part (b). Some candidates did not check that their GDC was set in degree mode while others treated the triangle as if it were right angled. A large number of candidates were penalized for not leaving their answers exactly or to three significant figures.

