| Date | May 2010 | Marks available | 6 | Reference code | 10M.2.sl.TZ2.8 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find and Hence | Question number | 8 | Adapted from | N/A |
Question
The diagram below shows a circle with centre O and radius 8 cm.
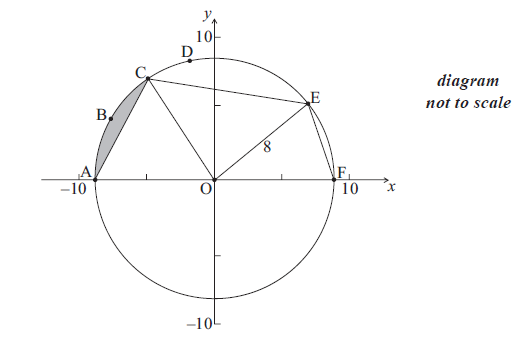
The points A, B, C, D, E and F are on the circle, and [AF] is a diameter. The length of arc ABC is 6 cm.
Find the size of angle AOC .
Hence find the area of the shaded region.
The area of sector OCDE is \(45{\text{ c}}{{\text{m}}^2}\).
Find the size of angle COE .
Find EF .
Markscheme
appropriate approach (M1)
e.g. \(6 = 8\theta \)
\({\rm{A}}\widehat {\rm{O}}{\rm{C}} = 0.75\) A1 N2
[2 marks]
evidence of substitution into formula for area of triangle (M1)
e.g. \({\rm{area}} = \frac{1}{2} \times 8 \times 8 \times \sin (0.75)\)
area \(= 21.8 \ldots \) (A1)
evidence of substitution into formula for area of sector (M1)
e.g. \({\rm{area}} = \frac{1}{2} \times 64 \times 0.75\)
area of sector \(= 24\) (A1)
evidence of substituting areas (M1)
e.g. \(\frac{1}{2}{r^2}\theta - \frac{1}{2}ab\sin C\) , \({\text{area of sector}} - {\text{area of triangle}}\)
area of shaded region \( = 2.19{\text{ c}}{{\text{m}}^2}\) A1 N4
[6 marks]
attempt to set up an equation for area of sector (M1)
e.g. \(45 = \frac{1}{2} \times {8^2} \times \theta \)
\({\rm{C}}\widehat {\rm{O}}{\rm{E}} = 1.40625\) (1.41 to 3 sf) A1 N2
[2 marks]
METHOD 1
attempting to find angle EOF (M1)
e.g. \(\pi - 0.75 - 1.41\)
\({\rm{E}}\widehat {\rm{O}}{\rm{F}} = 0.985\) (seen anywhere) A1
evidence of choosing cosine rule (M1)
correct substitution A1
e.g. \({\rm{EF}} = \sqrt {{8^2} + {8^2} - 2 \times 8 \times 8 \times \cos 0.985} \)
EF \(= 7.57{\text{ cm}}\) A1 N3
METHOD 2
attempting to find angles that are needed (M1)
e.g. angle EOF and angle OEF
\({\rm{E}}\widehat {\rm{O}}{\rm{F}} = 0.9853 \ldots \) and \({\text{O}}\widehat {\rm{E}}{\text{F (or O}}\widehat {\text{F}}{\text{E)}} = 1.078 \ldots \) A1
evidence of choosing sine rule (M1)
correct substitution (A1)
e.g. \(\frac{{{\rm{EF}}}}{{\sin 0.985}} = \frac{8}{{\sin 1.08}}\)
EF \(= 7.57{\text{ cm}}\) A1 N3
METHOD 3
attempting to find angle EOF (M1)
e.g. \(\pi - 0.75 - 1.41\)
\({\rm{E}}\widehat {\rm{O}}{\rm{F}} = 0.985\) (seen anywhere) A1
evidence of using half of triangle EOF (M1)
e.g. \(x = 8\sin \frac{{0.985}}{2}\)
correct calculation A1
e.g. \(x = 3.78\)
EF \(= 7.57{\text{ cm}}\) A1 N3
[5 marks]
Examiners report
Most candidates demonstrated understanding of trigonometry on this question. They generally did well in parts (a) and (c), and even many of them on part (b). Fewer candidates could do part (d).
Many opted to work in degrees rather than in radians, which often introduced multiple inaccuracies. Some worked with an incorrect radius of 6 or 10.
A pleasing number knew how to find the area of the shaded region.
Inability to work in radians and misunderstanding of significant figures were common problems, though. Weaker candidates often made the mistake of using triangle formulae for sectors or used degrees in the formulas instead of radians.
For some candidates there were many instances of confusion between lines and arcs. In (a) some treated 6 as the length of AC . In (d) some found the length of arc EF rather than the length of the segment.
Several students seemed to confuse the area of sector in (b) with the shaded region.
Most candidates demonstrated understanding of trigonometry on this question. They generally did well in parts (a) and (c), and even many of them on part (b). Fewer candidates could do part (d).
Many opted to work in degrees rather than in radians, which often introduced multiple inaccuracies. Some worked with an incorrect radius of 6 or 10.
A pleasing number knew how to find the area of the shaded region.
Inability to work in radians and misunderstanding of significant figures were common problems, though. Weaker candidates often made the mistake of using triangle formulae for sectors or used degrees in the formulas instead of radians.
For some candidates there were many instances of confusion between lines and arcs. In (a) some treated 6 as the length of AC . In (d) some found the length of arc EF rather than the length of the segment.
Several students seemed to confuse the area of sector in (b) with the shaded region.
Most candidates demonstrated understanding of trigonometry on this question. They generally did well in parts (a) and (c), and even many of them on part (b). Fewer candidates could do part (d).
Many opted to work in degrees rather than in radians, which often introduced multiple inaccuracies. Some worked with an incorrect radius of 6 or 10.
A pleasing number knew how to find the area of the shaded region.
Inability to work in radians and misunderstanding of significant figures were common problems, though. Weaker candidates often made the mistake of using triangle formulae for sectors or used degrees in the formulas instead of radians.
For some candidates there were many instances of confusion between lines and arcs. In (a) some treated 6 as the length of AC . In (d) some found the length of arc EF rather than the length of the segment.
Several students seemed to confuse the area of sector in (b) with the shaded region.
Most candidates demonstrated understanding of trigonometry on this question. They generally did well in parts (a) and (c), and even many of them on part (b). Fewer candidates could do part (d).
Many opted to work in degrees rather than in radians, which often introduced multiple inaccuracies. Some worked with an incorrect radius of 6 or 10.
A pleasing number knew how to find the area of the shaded region.
Inability to work in radians and misunderstanding of significant figures were common problems, though. Weaker candidates often made the mistake of using triangle formulae for sectors or used degrees in the formulas instead of radians.
For some candidates there were many instances of confusion between lines and arcs. In (a) some treated 6 as the length of AC . In (d) some found the length of arc EF rather than the length of the segment.
Several students seemed to confuse the area of sector in (b) with the shaded region.

