| Date | May 2017 | Marks available | 7 | Reference code | 17M.2.sl.TZ1.5 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
The following diagram shows the chord [AB] in a circle of radius 8 cm, where \({\text{AB}} = 12{\text{ cm}}\).
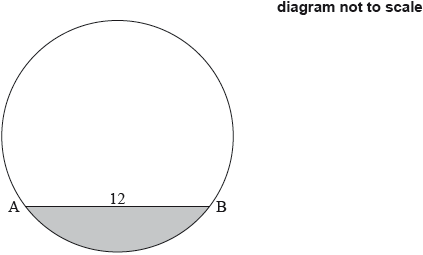
Find the area of the shaded segment.
Markscheme
attempt to find the central angle or half central angle (M1)
eg\(\,\,\,\,\,\)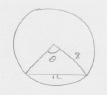 , cosine rule, right triangle
, cosine rule, right triangle
correct working (A1)
eg\(\,\,\,\,\,\)\(\cos \theta = \frac{{{8^2} + {8^2} - {{12}^2}}}{{2 \bullet 8 \bullet 8}},{\text{ }}{\sin ^{ - 1}}\left( {\frac{6}{8}} \right),{\text{ }}0.722734,{\text{ }}41.4096^\circ ,{\text{ }}\frac{\pi }{2} - {\sin ^{ - 1}}\left( {\frac{6}{8}} \right)\)
correct angle \({\rm{A\hat OB}}\) (seen anywhere)
eg\(\,\,\,\,\,\)\({\text{1.69612, }}97.1807^\circ ,{\text{ 2}} \times {\text{si}}{{\text{n}}^{ - 1}}\left( {\frac{6}{8}} \right)\) (A1)
correct sector area
eg\(\,\,\,\,\,\)\(\frac{1}{2}(8)(8)(1.70),{\text{ }}\frac{{97.1807}}{{360}}(64\pi ),{\text{ }}54.2759\) (A1)
area of triangle (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}(8)(8)\sin 1.70,{\text{ }}\frac{1}{2}(8)(12)\sin 0.722,{\text{ }}\frac{1}{2} \times \sqrt {64 - 36} \times 12,{\text{ }}31.7490\)
appropriate approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\({A_{{\text{triangle}}}} - {A_{{\text{sector}}}}\), their sector-their triangle
22.5269
area of shaded region \( = 22.5{\text{ }}({\text{c}}{{\text{m}}^2})\) A1 N4
Note: Award M0A0A0A0A1 then M1A0 (if appropriate) for correct triangle area without any attempt to find an angle in triangle OAB.
[7 marks]

