| Date | November 2015 | Marks available | 3 | Reference code | 15N.2.sl.TZ0.8 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
The following diagram shows the quadrilateral \(ABCD\).
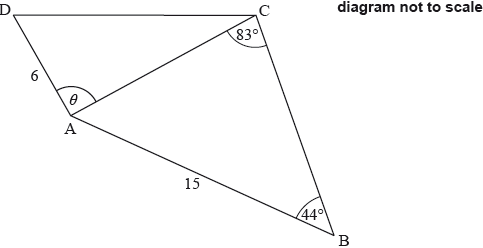
\[{\text{AD}} = 6{\text{ cm}},{\text{ AB}} = 15{\text{ cm}},{\rm{ A\hat BC}} = 44^\circ ,{\rm{ A\hat CB}} = 83^\circ {\rm{ and D\hat AC}} = \theta \]
Find \(AC\).
Find the area of triangle \(ABC\).
The area of triangle \(ACD\) is half the area of triangle \(ABC\).
Find the possible values of \(\theta \).
Given that \(\theta \) is obtuse, find \(CD\).
Markscheme
evidence of choosing sine rule (M1)
eg\(\;\;\;\frac{{{\text{AC}}}}{{\sin {\rm{C\hat BA}}}} = \frac{{{\text{AB}}}}{{\sin {\rm{A\hat CB}}}}\)
correct substitution (A1)
eg\(\;\;\;\frac{{{\text{AC}}}}{{\sin 44^\circ }} = \frac{{15}}{{\sin 83^\circ }}\)
\(10.4981\)
\({\text{AC}} = 10.5{\text{ }}{\text{ (cm)}}\) A1 N2
[3 marks]
finding \({\rm{C\hat AB}}\) (seen anywhere) (A1)
eg\(\;\;\;180^\circ - 44^\circ - 83^\circ ,{\rm{ C\hat AB}} = 53^\circ \)
correct substitution for area of triangle \(ABC\) A1
eg\(\;\;\;\frac{1}{2} \times 15 \times 10.4981 \times \sin 53^\circ \)
62.8813
\({\text{area}} = 62.9{\text{ }}{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1 N2
[3 marks]
correct substitution for area of triangle \(DAC\) (A1)
eg\(\;\;\;\frac{1}{2} \times 6 \times 10.4981 \times \sin \theta \)
attempt to equate area of triangle \(ACD\) to half the area of triangle \(ABC\) (M1)
eg\(\;\;\;{\text{area ACD}} = \frac{1}{2} \times {\text{ area ABC; 2ACD}} = {\text{ABC}}\)
correct equation A1
eg\(\;\;\;\frac{1}{2} \times 6 \times 10.4981 \times \sin \theta = \frac{1}{2}(62.9),{\text{ }}62.9887\sin \theta = 62.8813,{\text{ }}\sin \theta = 0.998294\)
\(86.6531\), \(93.3468\)
\(\theta = 86.7^\circ {\text{ }},{\text{ }}\theta = 93.3^\circ {\text{ }}\) A1A1 N2
[5 marks]
Note: Note: If candidates use an acute angle from part (c) in the cosine rule, award M1A0A0 in part (d).
evidence of choosing cosine rule (M1)
eg\(\;\;\;{\text{C}}{{\text{D}}^2} = {\text{A}}{{\text{D}}^2} + {\text{A}}{{\text{C}}^2} - 2 \times {\text{AD}} \times {\text{AC}} \times \cos \theta \)
correct substitution into rhs (A1)
eg\(\;\;\;{\text{C}}{{\text{D}}^2} = {6^2} + {10.498^2} - 2(6)(10.498)\cos 93.336^\circ \)
\(12.3921\)
\(12.4{\text{ }}{\text{ (cm)}}\) A1 N2
[3 marks]
Total [14 marks]

