| Date | May 2016 | Marks available | 3 | Reference code | 16M.2.sl.TZ2.2 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Question number | 2 | Adapted from | N/A |
Question
The following diagram shows a quadrilateral ABCD.
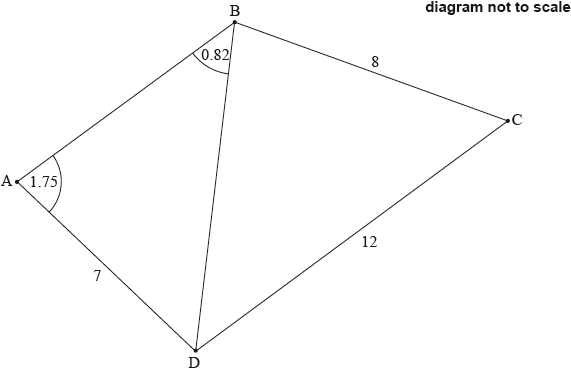
\[{\text{AD}} = {\text{7}}\;{\text{cm,}}\;{\text{BC}} = {\text{8}}\;{\text{cm,}}\;{\text{CD}} = {\text{12}}\;{\text{cm,}}\;{\rm{D\hat AB}} = {\text{1.75}}\;{\text{radians,}}\;{\rm{A\hat BD}} = {\text{0.82}}\;{\text{radians.}}\]
Find BD.
Find \({\rm{D\hat BC}}\).
Markscheme
evidence of choosing sine rule (M1)
eg\(\,\,\,\,\,\)\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(\frac{a}{{\sin 1.75}} = \frac{7}{{\sin 0.82}}\)
9.42069
\({\text{BD}} = 9.42{\text{ (cm)}}\) A1 N2
[3 marks]
evidence of choosing cosine rule (M1)
eg\(\,\,\,\,\,\)\(\cos B = \frac{{{d^2} + {c^2} - {b^2}}}{{2dc}},{\text{ }}{a^2} = {b^2} + {c^2} - 2bc\cos B\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(\frac{{{8^2} + {{9.42069}^2} - {{12}^2}}}{{2 \times 8 \times 9.42069}},{\text{ }}144 = 64 + {\text{B}}{{\text{D}}^2} - 16{\text{BD}}\cos B\)
1.51271
\({\rm{D\hat BC}} = 1.51\) (radians) (accept 86.7°) A1 N2
[3 marks]
Examiners report
Most candidates solved part (a) correctly, recognizing the need for the law of sines.
In part (b), some recognized they had to use cosine rule but substituted incorrectly. There were a few who used Pythagoras theorem or overly long approaches using the sine rule for 2(b).
Some used the calculator in degree mode instead of radian mode, not recognizing that the angles were given in radians.

