| Date | May 2010 | Marks available | 6 | Reference code | 10M.2.sl.TZ1.8 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find and Hence | Question number | 8 | Adapted from | N/A |
Question
The diagram below shows a quadrilateral ABCD with obtuse angles \({\rm{A}}\widehat {\rm{B}}{\rm{C}}\) and \({\rm{A}}\widehat {\rm{D}}{\rm{C}}\).
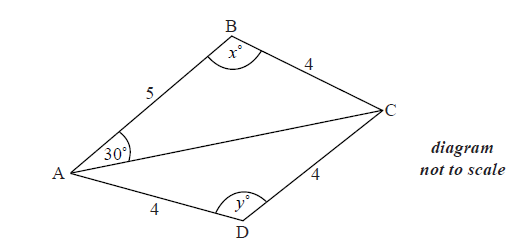
AB = 5 cm, BC = 4 cm, CD = 4 cm, AD = 4 cm , \({\rm{B}}\widehat {\rm{A}}{\rm{C}} = {30^ \circ }\) , \({\rm{A}}\widehat {\rm{B}}{\rm{C}} = {x^ \circ }\) , \({\rm{A}}\widehat {\rm{D}}{\rm{C}} = {y^ \circ }\) .
Use the cosine rule to show that \({\rm{AC}} = \sqrt {41 - 40\cos x} \) .
Use the sine rule in triangle ABC to find another expression for AC.
(i) Hence, find x, giving your answer to two decimal places.
(ii) Find AC .
(i) Find y.
(ii) Hence, or otherwise, find the area of triangle ACD.
Markscheme
correct substitution A1
e.g. \(25 + 16 - 40\cos x\) , \({5^2} + {4^2} - 2 \times 4 \times 5\cos x\)
\({\rm{AC}} = \sqrt {41 - 40\cos x} \) AG
[1 mark]
correct substitution A1
e.g. \(\frac{{{\rm{AC}}}}{{\sin x}} = \frac{4}{{\sin 30}}\) , \(\frac{1}{2}{\rm{AC}} = 4\sin x\)
\({\rm{AC}} = 8\sin x\) (accept \(\frac{{4\sin x}}{{\sin 30}}\)) A1 N1
[2 marks]
(i) evidence of appropriate approach using AC M1
e.g. \(8\sin x = \sqrt {41 - 40\cos x} \) , sketch showing intersection
correct solution \(8.682 \ldots \), \(111.317 \ldots \) (A1)
obtuse value \(111.317 \ldots \) (A1)
\(x = 111.32\) to 2 dp (do not accept the radian answer 1.94 ) A1 N2
(ii) substituting value of x into either expression for AC (M1)
e.g. \({\rm{AC}} = 8\sin 111.32\)
\({\rm{AC}} = 7.45\) A1 N2
[6 marks]
(i) evidence of choosing cosine rule (M1)
e.g. \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)
correct substitution A1
e.g. \(\frac{{{4^2} + {4^2} - {{7.45}^2}}}{{2 \times 4 \times 4}}\) , \({7.45^2} = 32 - 32\cos y\) , \(\cos y = - 0.734 \ldots \)
\(y = 137\) A1 N2
(ii) correct substitution into area formula (A1)
e.g. \(\frac{1}{2} \times 4 \times 4 \times \sin 137\) , \(8\sin 137\)
area \(= 5.42\) A1 N2
[5 marks]
Examiners report
Many candidates worked comfortably with the sine and cosine rules in part (a) and (b).
Many candidates worked comfortably with the sine and cosine rules in part (a) and (b). Equally as many did not take the cue from the word "hence" and used an alternate method to solve the problem and thus did not receive full marks. Those who managed to set up an equation, again did not go directly to their GDC but rather engaged in a long, laborious analytical approach that was usually unsuccessful.
Equally as many did not take the cue from the word "hence" and used an alternate method to solve the problem and thus did not receive full marks. Those who managed to set up an equation, again did not go directly to their GDC but rather engaged in a long, laborious analytical approach that was usually unsuccessful. No matter what values were found in (c) (i) most candidates recovered and earned follow through marks for the remainder of the question. A large number of candidates worked in the wrong mode and rounded prematurely throughout this question often resulting in accuracy penalties.
Equally as many did not take the cue from the word "hence" and used an alternate method to solve the problem and thus did not receive full marks. Those who managed to set up an equation, again did not go directly to their GDC but rather engaged in a long, laborious analytical approach that was usually unsuccessful. No matter what values were found in (c) (i) most candidates recovered and earned follow through marks for the remainder of the question. A large number of candidates worked in the wrong mode and rounded prematurely throughout this question often resulting in accuracy penalties.

