| Date | May 2015 | Marks available | 4 | Reference code | 15M.2.sl.TZ2.10 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Show that | Question number | 10 | Adapted from | N/A |
Question
The following diagram shows a square \(ABCD\), and a sector \(OAB\) of a circle centre \(O\), radius \(r\). Part of the square is shaded and labelled \(R\).
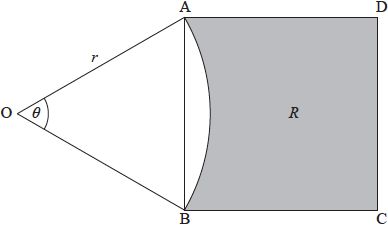
\[{\rm{A\hat OB}} = \theta {\text{, where }}0.5 \ \le \ \theta < \pi .\]
Show that the area of the square \(ABCD\) is \(2{r^2}(1 - \cos \theta )\).
When \(\theta = \alpha \), the area of the square \(ABCD\) is equal to the area of the sector \(OAB\).
(i) Write down the area of the sector when \(\theta = \alpha \).
(ii) Hence find \(\alpha \).
When \(\theta = \beta \), the area of \(R\) is more than twice the area of the sector.
Find all possible values of \(\beta \).
Markscheme
area of \({\text{ABCD}} = {\text{A}}{{\text{B}}^2}\) (seen anywhere) (A1)
choose cosine rule to find a side of the square (M1)
eg\(\;\;\;{a^2} = {b^2} + {c^2} - 2bc\cos \theta \)
correct substitution (for triangle \(AOB\)) A1
eg\(\;\;\;{r^2} + {r^2} - 2 \times r \times r\cos \theta ,{\text{ O}}{{\text{A}}^2} + {\text{O}}{{\text{B}}^2} - 2 \times {\text{OA}} \times {\text{OB}}\cos \theta \)
correct working for \({\text{A}}{{\text{B}}^2}\) A1
eg\(\;\;\;2{r^{\text{2}}} - 2{r^2}\cos \theta \)
\({\text{area}} = 2{r^2}(1 - \cos \theta )\) AG N0
Note: Award no marks if the only working is \(2{r^2} - 2{r^2}\cos \theta \).
[4 marks]
(i) \(\frac{1}{2}\alpha {r^2}\;\;\;\left( {{\text{accept }}2{r^2}(1 - \cos \alpha )} \right)\) A1 N1
(ii) correct equation in one variable (A1)
eg\(\;\;\;2(1 - \cos \alpha ) = \frac{1}{2}\alpha \)
\(\alpha = 0.511024\)
\(\alpha = 0.511\;\;\;({\text{accept }}\theta = 0.511)\) A2 N2
Note: Award A1 for \(\alpha = 0.511\) and additional answers.
[4 marks]
Note: In this part, accept \(\theta \) instead of \(\beta \), and the use of equations instead of inequalities in the working.
attempt to find \(R\) (M1)
eg\(\;\;\;\)subtraction of areas, \({\text{square}} - {\text{segment}}\)
correct expression for segment area (A1)
eg\(\;\;\;\frac{1}{2}\beta {r^2} - \frac{1}{2}{r^2}\sin \beta \)
correct expression for \(R\) (A1)
eg\(\;\;\;2{r^2}(1 - \cos \beta ) - \left( {\frac{1}{2}\beta {r^2} - \frac{1}{2}{r^2}\sin \beta } \right)\)
correct inequality (A1)
eg\(\;\;\;2{r^2}(1 - \cos \beta ) - \left( {\frac{1}{2}\beta {r^2} - \frac{1}{2}{r^2}\sin \beta } \right) > 2\left( {\frac{1}{2}\beta {r^2}} \right)\)
correct inequality in terms of angle only A1
eg\(\;\;\;2(1 - \cos \beta ) - \left( {\frac{1}{2}\beta - \frac{1}{2}\sin \beta } \right) > \beta \)
attempt to solve their inequality, must represent \(R > \) twice sector (M1)
eg\(\;\;\;\)sketch, one correct value
Note: Do not award the second (M1) unless the first (M1) for attempting to find \(R\) has been awarded.
both correct values \(1.30573\) and \(2.67369\) (A1)
correct inequality \(1.31 < \beta < 2.67\) A1 N3
[8 marks]
Total [16 marks]
Examiners report
Those who attempted part (a) could in general show what was required by using the cosine rule. On rare occasions some more complicated approaches were seen using half of angle theta. In some cases, candidates did not show all the necessary steps and lost marks for not completely showing the given result.
A number of candidates correctly answered part (bi) and created a correct equation in (bii), but did not solve the equation correctly, usually attempting an analytic method where the GDC would do. For many a major problem was to realize the need to reduce the equation to one variable before attempting to solve it. Occasionally, an answer would be written that was outside the given domain.
When part (c) was attempted, many candidates did not recognize that the area in question requires the subtraction of a segment area, and often set the square area greater than twice the sector. Many candidates made mistakes when trying to eliminate brackets or just did not use them. Of those who created a correct inequality, few reached a fully correct conclusion.

