| Date | May 2012 | Marks available | 4 | Reference code | 12M.2.sl.TZ2.10 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Show that | Question number | 10 | Adapted from | N/A |
Question
Consider the following circle with centre O and radius r .
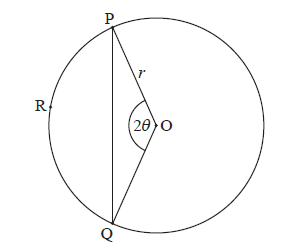
The points P, R and Q are on the circumference, \({\rm{P}}\widehat {\rm{O}}{\rm{Q}} = 2\theta \) , for \(0 < \theta < \frac{\pi }{2}\) .
Use the cosine rule to show that \({\rm{PQ}} = 2r\sin \theta \) .
Let l be the length of the arc PRQ .
Given that \(1.3{\rm{PQ}} - l = 0\) , find the value of \(\theta \) .
Consider the function \(f(\theta ) = 2.6\sin \theta - 2\theta \) , for \(0 < \theta < \frac{\pi }{2}\) .
(i) Sketch the graph of f .
(ii) Write down the root of \(f(\theta ) = 0\) .
Use the graph of f to find the values of \(\theta \) for which \(l < 1.3{\rm{PQ}}\) .
Markscheme
correct substitution into cosine rule A1
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = {r^2} + {r^2} - 2(r)(r)\cos (2\theta )\) , \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} - 2{r^2}(\cos (2\theta ))\)
substituting \(1 - 2{\sin ^2}\theta \) for \(\cos 2\theta \) (seen anywhere) A1
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} - 2{r^2}(1 - 2{\sin ^2}\theta )\)
working towards answer (A1)
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} - 2{r^2} + 4{r^2}{\sin ^2}\theta \)
recognizing \(2{r^2} - 2{r^2} = 0\) (including crossing out) (seen anywhere)
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 4{r^2}{\sin ^2}\theta \) , \({\rm{PQ}} = \sqrt {4{r^2}{{\sin }^2}\theta } \)
\({\rm{PQ = 2}}r{\rm{sin}}\theta \) AG N0
[4 marks]
\({\rm{PRQ}} = r \times 2\theta \) (seen anywhere) (A1)
correct set up A1
e.g. \(1.3 \times 2r\sin \theta - r \times (2\theta ) = 0\)
attempt to eliminate r (M1)
correct equation in terms of the one variable \(\theta \) (A1)
e.g. \(1.3 \times 2\sin \theta - 2\theta = 0\)
1.221496215
\(\theta = 1.22\) (accept \(70.0^\circ \) (69.9)) A1 N3
[5 marks]
(i)
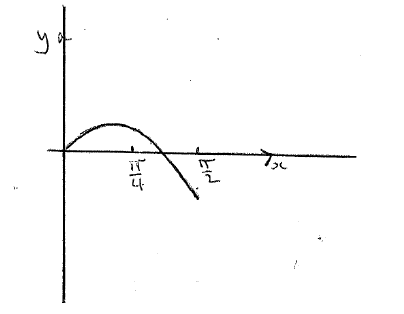 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for approximately correct shape, A1 for x-intercept in approximately correct position, A1 for domain. Do not penalise if sketch starts at origin.
(ii) \(1.221496215\)
\(\theta = 1.22\) A1 N1
[4 marks]
evidence of appropriate approach (may be seen earlier) M2
e.g. \(2\theta < 2.6\sin \theta \) , \(0 < f(\theta )\) , showing positive part of sketch
\(0 < \theta < 1.221496215\)
\(0 < \theta = 1.22\) (accept \(\theta < 1.22\) ) A1 N1
[3 marks]
Examiners report
This exercise seemed to be challenging for the great majority of the candidates, in particular parts (b), (c) and (d).
Part (a) was generally attempted using the cosine rule, but many failed to substitute correctly into the right hand side or skipped important steps. A high percentage could not arrive at the given expression due to a lack of knowledge of trigonometric identities or making algebraic errors, and tried to force their way to the given answer.
The most common errors included taking the square root too soon, and sign errors when distributing the negative after substituting \(\cos 2\theta \) by \(1 - 2{\sin ^2}\theta \) .
This exercise seemed to be challenging for the great majority of the candidates, in particular parts (b), (c) and (d).
In part (b), most candidates understood what was required but could not find the correct length of the arc PRQ mainly due to substituting the angle by \(\theta \) instead of \(2\theta \) .
Regarding part (c), many valid approaches were seen for the graph of f, making a good use of their GDC. A common error was finding a second or third solution outside the domain. A considerable amount of sketches were missing a scale.
There were candidates who achieved the correct equation but failed to realize they could use their GDC to solve it.
Part (d) was attempted by very few, and of those who achieved the correct answer not many were able to show the method they used.

