| Date | November 2017 | Marks available | 3 | Reference code | 17N.1.sl.TZ0.4 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The following diagram shows triangle ABC, with \({\text{AB}} = 3{\text{ cm}}\), \({\text{BC}} = 8{\text{ cm}}\), and \({\rm{A\hat BC = }}\frac{\pi }{3}\).
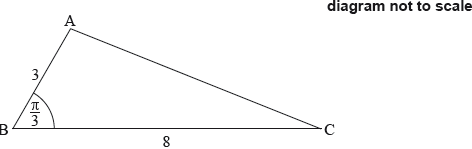
Show that \({\text{AC}} = 7{\text{ cm}}\).
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.
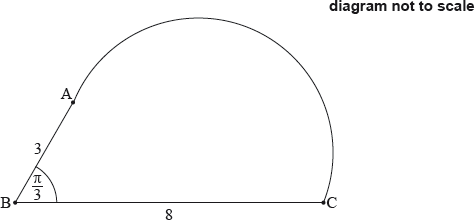
Find the exact perimeter of this shape.
Markscheme
evidence of choosing the cosine rule (M1)
eg\(\,\,\,\,\,\)\({c^2} = {a^2} + {b^2} - ab\cos C\)
correct substitution into RHS of cosine rule (A1)
eg\(\,\,\,\,\,\)\({3^2} + {8^2} - 2 \times 3 \times 8 \times \cos \frac{\pi }{3}\)
evidence of correct value for \(\cos \frac{\pi }{3}\) (may be seen anywhere, including in cosine rule) A1
eg\(\,\,\,\,\,\)\(\cos \frac{\pi }{3} = \frac{1}{2},{\text{ A}}{{\text{C}}^2} = 9 + 64 - \left( {48 \times \frac{1}{2}} \right),{\text{ }}9 + 64 - 24\)
correct working clearly leading to answer A1
eg\(\,\,\,\,\,\)\({\text{A}}{{\text{C}}^2} = 49,{\text{ }}b = \sqrt {49} \)
\({\text{AC}} = 7{\text{ (cm)}}\) AG N0
Note: Award no marks if the only working seen is \({\text{A}}{{\text{C}}^2} = 49\) or \({\text{AC}} = \sqrt {49} \) (or similar).
[4 marks]
correct substitution for semicircle (A1)
eg\(\,\,\,\,\,\)\({\text{semicircle}} = \frac{1}{2}(2\pi \times 3.5),{\text{ }}\frac{1}{2} \times \pi \times 7,{\text{ }}3.5\pi \)
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\({\text{perimeter}} = {\text{AB}} + {\text{BC}} + {\text{semicircle, }}3 + 8 + \left( {\frac{1}{2} \times 2 \times \pi \times \frac{7}{2}} \right),{\text{ }}8 + 3 + 3.5\pi \)
\(11 + \frac{7}{2}\pi {\text{ }}( = 3.5\pi + 11){\text{ (cm)}}\) A1 N2
[3 marks]

