| Date | May 2009 | Marks available | 3 | Reference code | 09M.2.sl.TZ1.2 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The circle shown has centre O and radius 3.9 cm.
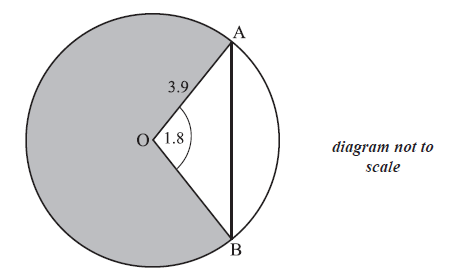
Points A and B lie on the circle and angle AOB is 1.8 radians.
Find AB.
Find the area of the shaded region.
Markscheme
METHOD 1
choosing cosine rule (M1)
substituting correctly A1
e.g. \({\rm{AB}} = \sqrt {{{3.9}^2} + {{3.9}^2} - 2(3.9)(3.9)\cos 1.8} \)
\({\rm{AB}} = 6.11\) (cm) A1 N2
METHOD 2
evidence of approach involving right-angled triangles (M1)
substituting correctly A1
e.g. \(\sin 0.9 = \frac{x}{{3.9}}\) , \(\frac{1}{2}{\rm{AB}} = 3.9\sin 0.9\)
\({\rm{AB}} = 6.11\) (cm) A1 N2
METHOD 3
choosing the sine rule (M1)
substituting correctly A1
e.g. \(\frac{{\sin 0.670 \ldots }}{{3.9}} = \frac{{\sin 1.8}}{{{\rm{AB}}}}\)
\({\rm{AB}} = 6.11\) (cm) A1 N2
[3 marks]
METHOD 1
reflex \({\rm{A}}\widehat {\rm{O}}{\rm{B}} = 2\pi - 1.8\) \(( = 4.4832)\) (A2)
correct substitution \(A = \frac{1}{2}{(3.9)^2}(4.4832 \ldots )\) A1
area =34.1 (cm2) A1 N2
METHOD 2
finding area of circle \(A = \pi {(3.9)^2}\) \(( = 47.78 \ldots )\) (A1)
finding area of (minor) sector \(A = \frac{1}{2}{(3.9)^2}(1.8)\) \(( = 13.68 \ldots )\) (A1)
subtracting M1
e.g. \(\pi {(3.9)^2} - 0.5{(3.9)^2}(1.8)\) , \(47.8 - 13.7\)
area = 34.1 (cm2) A1 N2
METHOD 3
finding reflex \({\rm{A}}\widehat {\rm{O}}{\rm{B}} = 2\pi - 1.8\) \(( = 4.4832)\) (A2)
finding proportion of total area of circle A1
e.g. \(\frac{{2\pi - 1.8}}{{2\pi }} \times \pi {(3.9)^2}\) , \(\frac{\theta }{{2\pi }} \times \pi {r^2}\)
area = 34.1 (cm2) A1 N2
[4 marks]
Examiners report
This question was well answered by the majority of candidates. Full solutions were common in both parts, and a variety of successful approaches were used. Radians were well handled with few candidates working with the angle in degrees. Some candidates incorrectly found the length of the arc subtended by the central angle rather than the length of segment [AB].
In part (b), some candidates incorrectly subtracted the area of the triangle or even a length. Many candidates failed to give answers to 3 significant figures and therefore lost an accuracy mark.

