| Date | May 2014 | Marks available | 3 | Reference code | 14M.2.sl.TZ1.1 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows triangle ABC.
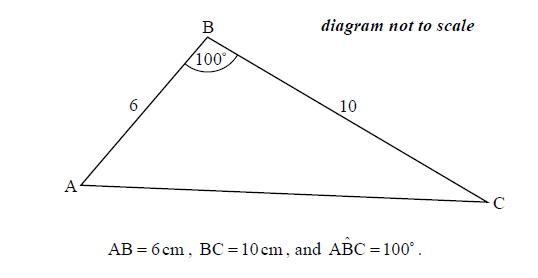
Find AC.
Find \({\rm{B\hat CA}}\).
Markscheme
evidence of choosing cosine rule (M1)
eg \({\text{A}}{{\text{C}}^2} = {\text{A}}{{\text{B}}^2} + {\text{B}}{{\text{C}}^2} - 2({\text{AB}})({\text{BC}})\cos ({\rm{A\hat BC}})\)
correct substitution into the right-hand side (A1)
eg \({6^2} + {10^2} - 2(6)(10)\cos {100^ \circ }\)
\({\text{AC}} = 12.5234\)
\({\text{AC}} = 12.5{\text{ (cm)}}\) A1 N2
[3 marks]
evidence of choosing a valid approach (M1)
eg sine rule, cosine rule
correct substitution (A1)
eg \(\frac{{\sin ({\rm{B\hat CA)}}}}{6} = \frac{{\sin 100^\circ }}{{12.5}},{\text{ }}\cos ({\rm{B\hat CA)}} = \frac{{{{({\text{AC}})}^2} + {{10}^2} - {6^2}}}{{2({\text{AC}})(10)}}\)
\({\rm{B\hat CA}} = 28.1525\)
\({\rm{B\hat CA}} = 28.2^\circ\) A1 N2
[3 marks]

