| Date | May 2017 | Marks available | 2 | Reference code | 17M.2.sl.TZ2.9 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
A ship is sailing north from a point A towards point D. Point C is 175 km north of A. Point D is 60 km north of C. There is an island at E. The bearing of E from A is 055°. The bearing of E from C is 134°. This is shown in the following diagram.
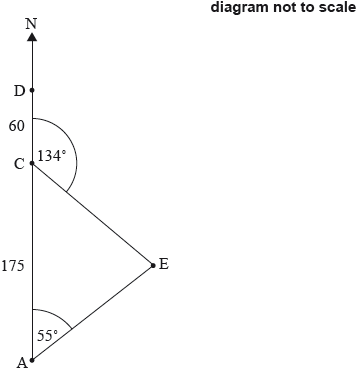
Find the bearing of A from E.
Finds CE.
Find DE.
When the ship reaches D, it changes direction and travels directly to the island at 50 km per hour. At the same time as the ship changes direction, a boat starts travelling to the island from a point B. This point B lies on (AC), between A and C, and is the closest point to the island. The ship and the boat arrive at the island at the same time. Find the speed of the boat.
Markscheme
valid method (M1)
eg\(\,\,\,\,\,\)\(180 + 55,{\text{ }}360 - 90 - 35\)
235° (accept S55W, W35S) A1 N2
[2 marks]
valid approach to find \({\rm{A\hat EC}}\) (may be seen in (a)) (M1)
eg\(\,\,\,\,\,\)\({\rm{A\hat EC}} = 180 - 55 - {\rm{A\hat CE}},{\text{ }}134 = {\text{E}} + 55\)
correct working to find \({\rm{A\hat EC}}\) (may be seen in (a)) (A1)
eg\(\,\,\,\,\,\)\(180 - 55 - 46,{\text{ }}134 - 55\), \({\rm{A\hat EC}} = 79^\circ \)
evidence of choosing sine rule (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)
correct substitution into sine rule (A1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{CE}}}}{{\sin 55^\circ }} = \frac{{175}}{{\sin {\rm{A\hat EC}}}}\)
146.034
\({\text{CE}} = 146{\text{ (km)}}\) A1 N2
[5 marks]
evidence of choosing cosine rule (M1)
eg\(\,\,\,\,\,\)\({\text{D}}{{\text{E}}^2} = {\text{D}}{{\text{C}}^2} + {\text{C}}{{\text{E}}^2} - 2 \times {\text{DC}} \times {\text{CE}} \times \cos \theta \)
correct substitution into right-hand side (A1)
eg\(\,\,\,\,\,\)\({60^2} + {146.034^2} - 2 \times 60 \times 146.034\cos 134\)
192.612
\({\text{DE}} = 193{\text{ (km)}}\) A1 N2
[3 marks]
valid approach for locating B (M1)
eg\(\,\,\,\,\,\)BE is perpendicular to ship’s path, angle \({\text{B}} = 90\)
correct working for BE (A1)
eg\(\,\,\,\,\,\)\(\sin 46^\circ = \frac{{{\text{BE}}}}{{146.034}},{\text{ BE}} = 146.034\sin 46^\circ ,{\text{ }}105.048\)
valid approach for expressing time (M1)
eg\(\,\,\,\,\,\)\(t = \frac{d}{s},{\text{ }}t = \frac{d}{r},{\text{ }}t = \frac{{192.612}}{{50}}\)
correct working equating time (A1)
eg\(\,\,\,\,\,\)\(\frac{{146.034\sin 46^\circ }}{r} = \frac{{192.612}}{{50}},{\text{ }}\frac{s}{{105.048}} = \frac{{50}}{{192.612}}\)
27.2694
27.3 (km per hour) A1 N3
[5 marks]

